المعادلات المعقدة مع معامل. حل المعادلات مع المعامل
حل المعادلات والمتباينات بالمعاملغالبا ما يسبب صعوبات. ومع ذلك، إذا كنت تفهم جيدا ما هو عليه القيمة المطلقة للرقم، و كيفية توسيع التعبيرات التي تحتوي على علامة معامل بشكل صحيح، ثم التواجد في المعادلة التعبير تحت علامة المعامل، ولم يعد يشكل عائقا أمام حلها.
القليل من النظرية. ولكل رقم خاصيتان: القيمة المطلقة للرقم وعلامته.
على سبيل المثال، الرقم +5، أو ببساطة 5، يحتوي على علامة "+" وقيمة مطلقة قدرها 5.
يحتوي الرقم -5 على علامة "-" وقيمة مطلقة قدرها 5.
القيم المطلقة للأرقام 5 و -5 هي 5.
القيمة المطلقة للرقم x تسمى معامل الرقم ويشار إليها بالرمز |x|.
وكما نرى فإن مقياس العدد يساوي الرقم نفسه إذا كان هذا الرقم أكبر من أو يساوي الصفر، وإلى هذا الرقم مع الإشارة المعاكسة إذا كان هذا الرقم سالباً.
الأمر نفسه ينطبق على أي تعبيرات تظهر تحت علامة المعامل.
تبدو قاعدة توسيع الوحدة كما يلي:
|f(x)|= f(x) إذا كان f(x) ≥ 0، و
|f(x)|= - f(x)، إذا كان f(x)< 0
على سبيل المثال |x-3|=x-3، إذا كان x-3≥0 و|x-3|=-(x-3)=3-x، إذا كان x-3<0.
لحل معادلة تحتوي على تعبير تحت علامة المعامل، يجب عليك أولاً قم بتوسيع الوحدة وفقًا لقاعدة توسيع الوحدة.
ومن ثم تصبح المعادلة أو المتباينة إلى معادلتين مختلفتين موجودتين على فترتين رقميتين مختلفتين.
توجد معادلة واحدة على فترة رقمية يكون فيها التعبير تحت علامة المعامل غير سالب.
والمعادلة الثانية موجودة في الفترة التي يكون فيها التعبير تحت إشارة المقياس سالبًا.
دعونا نلقي نظرة على مثال بسيط.
دعونا نحل المعادلة:
|س-3|=-س 2 +4x-3
1. دعونا نفتح الوحدة.
|x-3|=x-3، إذا كان x-3≥0، أي إذا كان x≥3
|x-3|=-(x-3)=3-x إذا كان x-3<0, т.е. если х<3
2. لقد تلقينا فاصلين عدديين: x≥3 وx<3.
دعونا نفكر في المعادلات التي تحولت إليها المعادلة الأصلية في كل فترة:
أ) بالنسبة لـ x≥3 |x-3|=x-3، ويكون جرحنا بالشكل:
انتباه! هذه المعادلة موجودة فقط في الفترة x≥3!
دعونا نفتح الأقواس ونقدم مصطلحات مماثلة:
وحل هذه المعادلة.
هذه المعادلة لها جذور:
× 1 = 0، × 2 = 3
انتباه! بما أن المعادلة x-3=-x 2 +4x-3 موجودة فقط في الفترة x≥3، فنحن مهتمون فقط بتلك الجذور التي تنتمي إلى هذه الفترة. يتم استيفاء هذا الشرط فقط بواسطة x 2 = 3.
ب) عند س<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:
انتباه! هذه المعادلة موجودة فقط في الفترة x<3!
دعونا نفتح الأقواس ونقدم مصطلحات مماثلة. نحصل على المعادلة:
× 1 = 2، × 2 = 3
انتباه! بما أن المعادلة 3-x=-x 2 +4x-3 موجودة فقط في الفترة x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.
لذا: من الفترة الأولى نأخذ فقط الجذر x=3، ومن الفترة الثانية - الجذر x=2.
المعامل هو القيمة المطلقة للتعبير. للإشارة إلى الوحدة بطريقة أو بأخرى، من المعتاد استخدام الأقواس المستقيمة. القيمة المحاطة بين قوسين زوجيين هي القيمة المأخوذة من الوحدة النمطية. تتكون عملية حل أي وحدة من فتح تلك الأقواس المستقيمة للغاية، والتي تسمى في اللغة الرياضية الأقواس المعيارية. يتم الكشف عنها وفقًا لعدد معين من القواعد. أيضًا، بترتيب حل الوحدات، تم العثور على مجموعات قيم تلك التعبيرات التي كانت بين قوسين معياريين. في معظم الحالات، يتم توسيع الوحدة بطريقة بحيث يتلقى التعبير الذي كان نمطيًا فرعيًا القيم الموجبة والسالبة، بما في ذلك القيمة صفر. إذا بدأنا من الخصائص المحددة للوحدة، فسيتم في هذه العملية تجميع معادلات أو متباينات مختلفة من التعبير الأصلي، والتي تحتاج بعد ذلك إلى حلها. دعونا معرفة كيفية حل الوحدات.
عملية الحل
يبدأ حل الوحدة بكتابة المعادلة الأصلية مع الوحدة. للإجابة على سؤال كيفية حل المعادلات مع المعامل، تحتاج إلى فتحه بالكامل. لحل هذه المعادلة، يتم توسيع الوحدة. يجب النظر في جميع التعبيرات المعيارية. من الضروري تحديد قيم الكميات غير المعروفة المدرجة في تركيبتها، حيث يصبح التعبير المعياري بين قوسين صفرًا. للقيام بذلك، يكفي مساواة التعبير بين قوسين معياريين بالصفر، ثم حساب حل المعادلة الناتجة. يجب تسجيل القيم التي تم العثور عليها. بنفس الطريقة، تحتاج أيضًا إلى تحديد قيمة جميع المتغيرات غير المعروفة لجميع الوحدات في هذه المعادلة. بعد ذلك، عليك البدء في تحديد ودراسة جميع حالات وجود المتغيرات في التعبيرات عندما تكون مختلفة عن القيمة صفر. للقيام بذلك، تحتاج إلى كتابة بعض أنظمة المتباينات المقابلة لجميع وحدات المتباينة الأصلية. يجب كتابة المتباينات بحيث تغطي جميع القيم المتاحة والممكنة للمتغير الموجود على خط الأعداد. ثم تحتاج إلى رسم نفس خط الأعداد للتصور، والذي سيتم من خلاله رسم جميع القيم التي تم الحصول عليها لاحقًا.
يمكن الآن القيام بكل شيء تقريبًا عبر الإنترنت. الوحدة ليست استثناء للقاعدة. يمكنك حلها عبر الإنترنت على أحد الموارد الحديثة العديدة. كل قيم المتغير الموجودة في الوحدة الصفرية ستكون قيدًا خاصًا سيتم استخدامه في عملية حل المعادلة المعيارية. في المعادلة الأصلية، تحتاج إلى فتح جميع الأقواس المعيارية المتاحة، مع تغيير علامة التعبير بحيث تتزامن قيم المتغير المطلوب مع تلك القيم المرئية على خط الأعداد. يجب حل المعادلة الناتجة. يجب التحقق من قيمة المتغير الذي سيتم الحصول عليه أثناء حل المعادلة مقابل القيد الذي تحدده الوحدة نفسها. إذا كانت قيمة المتغير تحقق الشرط تمامًا، فهي صحيحة. يجب التخلص من جميع الجذور التي سيتم الحصول عليها أثناء حل المعادلة، ولكنها لن تتناسب مع القيود.
مدرسة MBOU الثانوية رقم 17، إيفانوفو
« المعادلات ذات المعامل"
التطوير المنهجي
تجميع وانتاج
مدرس رياضيات
ليبيديفا إن.في.20010
مذكرة توضيحية
الفصل 1 مقدمة
القسم 2. الخصائص الأساسية القسم 3. التفسير الهندسي لمفهوم معامل الرقم القسم 4. الرسم البياني للدالة y = |x| القسم 5. الاتفاقياتالفصل 2. حل المعادلات التي تحتوي على معامل
القسم 1. معادلات النموذج |F(x)| = م (أبسط) القسم 2. معادلات الصيغة F(|x|) = m القسم 3. معادلات النموذج |F(x)| = ز(خ) القسم 4. معادلات النموذج |F(x)| = ± F(x) (الأجمل) القسم 5. معادلات النموذج |F(x)| = |ز(س)| القسم 6. أمثلة على حل المعادلات غير القياسية القسم 7. معادلات النموذج |F(x)| + |ز(س)| = 0 القسم 8. معادلات النموذج |a 1 x ± b 1 | ± |أ 2 × ± في 2 | ± …|أ ن × ± في ن | = م القسم 9. المعادلات التي تحتوي على عدة وحداتالفصل 3. أمثلة على حل المعادلات المختلفة بالمعامل.
القسم 1. المعادلات المثلثية القسم 2. المعادلات الأسية القسم 3. المعادلات اللوغاريتمية القسم 4. المعادلات غير العقلانية القسم 5. المهام المتقدمة إجابات على التدريبات فهرسمذكرة توضيحية.
يعد مفهوم القيمة المطلقة (المعامل) للرقم الحقيقي أحد خصائصه الأساسية. ينتشر هذا المفهوم على نطاق واسع في أقسام مختلفة من العلوم الفيزيائية والرياضية والتقنية. في ممارسة تدريس دورات الرياضيات في المدارس الثانوية وفقًا لبرنامج وزارة الدفاع في الاتحاد الروسي، يتم مواجهة مفهوم "القيمة المطلقة للرقم" بشكل متكرر: في الصف السادس، تعريف الوحدة النمطية و يتم تقديم معناها الهندسي. في الصف الثامن يتكون مفهوم الخطأ المطلق، ويدرس حل أبسط المعادلات والمتباينات التي تحتوي على معامل، ويدرس خواص الجذر التربيعي الحسابي؛ في الصف الحادي عشر، تم العثور على المفهوم في قسم "الجذر ن-الدرجة الرابعة."تظهر تجربة التدريس أن الطلاب غالبًا ما يواجهون صعوبات في حل المهام التي تتطلب معرفة هذه المادة، وغالبًا ما يتخطونها دون البدء في إكمالها. كما تتضمن نصوص واجبات الامتحانات للصفين التاسع والحادي عشر واجبات مماثلة. بالإضافة إلى ذلك، تختلف المتطلبات التي تفرضها الجامعات على خريجي المدارس، أي على مستوى أعلى من متطلبات المناهج المدرسية. بالنسبة للحياة في المجتمع الحديث، فإن تكوين أسلوب تفكير رياضي، يتجلى في بعض المهارات العقلية، أمر مهم للغاية. في عملية حل المشكلات باستخدام الوحدات النمطية، يلزم القدرة على استخدام تقنيات مثل التعميم والمواصفات والتحليل والتصنيف والتنظيم والقياس. يتيح لك حل مثل هذه المهام اختبار معرفتك بالأقسام الرئيسية للدورة المدرسية ومستوى التفكير المنطقي ومهارات البحث الأولية. هذا العمل مخصص لأحد الأقسام - حل المعادلات التي تحتوي على وحدة نمطية. ويتكون من ثلاثة فصول. يعرض الفصل الأول المفاهيم الأساسية وأهم الاعتبارات النظرية. ويقترح الفصل الثاني تسعة أنواع رئيسية من المعادلات التي تحتوي على وحدة نمطية، ويناقش طرق حلها، ويفحص أمثلة على مستويات مختلفة من التعقيد. ويقدم الفصل الثالث معادلات أكثر تعقيدا وغير قياسية (مثلثية، أسية، لوغاريتمية وغير عقلانية). يوجد لكل نوع من المعادلات تمارين لحلها بشكل مستقل (الإجابات والتعليمات مرفقة). الغرض الرئيسي من هذا العمل هو تقديم المساعدة المنهجية للمعلمين في التحضير للدروس وتنظيم الدورات الاختيارية. يمكن أيضًا استخدام المادة كمساعدة تعليمية لطلاب المدارس الثانوية. المهام المقترحة في العمل مثيرة للاهتمام وليس من السهل دائمًا حلها، مما يجعل من الممكن جعل الدافع التعليمي لدى الطلاب أكثر وعيًا واختبار قدراتهم وزيادة مستوى إعداد خريجي المدارس لدخول الجامعات. يتضمن الاختيار المتمايز للتمارين المقترحة الانتقال من المستوى الإنجابي لإتقان المواد إلى المستوى الإبداعي، بالإضافة إلى فرصة تعليم كيفية تطبيق معرفتك عند حل المشكلات غير القياسية.الفصل 1 مقدمة.
القسم 1. تحديد القيمة المطلقة .
تعريف : القيمة المطلقة (المعامل) لعدد حقيقي أيسمى الرقم غير السالب : أأو -أ. تعيين: │ أ │ يقرأ الإدخال كما يلي: "معامل الرقم أ" أو "القيمة المطلقة للرقم أ"│ أ، إذا كان > 0
│أ│ = │ 0، إذا كانت أ = 0 (1)
│ - وإذا أأمثلة: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
- توسيع وحدة التعبير:
القسم 2. الخصائص الأساسية.
دعونا ننظر في الخصائص الأساسية للقيمة المطلقة. الخاصية رقم 1: الأرقام المتضادة لها وحدات متساوية، أي. │а│=│- а│دعونا نبين أن المساواة صحيحة. دعونا نكتب تعريف الرقم - أ : │- أ│= (2) دعونا نقارن بين المجموعتين (1) و (2). ومن الواضح أن تعريفات القيم المطلقة للأرقام أو - أتطابق. لذلك، │а│=│- а│عند النظر في الخصائص التالية، سنقتصر على صياغتها، حيث تم تقديم برهانها الخاصية رقم 2: القيمة المطلقة لمجموع عدد محدود من الأعداد الحقيقية لا تتجاوز مجموع القيم المطلقة للمصطلحات: │а 1 + а 2 +…+ а n │ ≥│а 1 │+│а 2 │ + … + │а ن │ العقار رقم 3: القيمة المطلقة للفرق بين رقمين حقيقيين لا تتجاوز مجموع قيمهما المطلقة: │а - в│ ≥│а│+│в│ العقار رقم 4: القيمة المطلقة لمنتج عدد محدود من الأعداد الحقيقية تساوي منتج القيم المطلقة للعوامل: │а·в│=│а│·│в│ العقار رقم 5: القيمة المطلقة لحاصل الأعداد الحقيقية تساوي حاصل قسمة قيمها المطلقة:
القسم 3. التفسير الهندسي لمفهوم معامل الرقم.
يمكن ربط كل عدد حقيقي بنقطة على خط الأعداد، والتي ستكون صورة هندسية لهذا الرقم الحقيقي. كل نقطة على خط الأعداد تتوافق مع بعدها عن نقطة الأصل، أي. طول القطعة من نقطة الأصل إلى نقطة معينة. تعتبر هذه المسافة دائمًا قيمة غير سالبة. ولذلك، فإن طول القطعة المقابلة سيكون التفسير الهندسي للقيمة المطلقة لعدد حقيقي معين
يؤكد الرسم الهندسي المعروض بوضوح الخاصية رقم 1، أي. معاملات الأعداد المتضادة متساوية. من هنا يمكن فهم صحة المساواة بسهولة: │kh – а│= │а – x│. يصبح حل المعادلة │x│= m، حيث m ≥ 0، أي x 1.2 = ± m، أكثر وضوحًا أيضًا. أمثلة: 1) │x│= 4 × 1.2 = ± 4 2) │x - 3│= 1
× 1.2 = 2؛ 4 القسم 4. الرسم البياني للدالة y = │kh│
مجال هذه الدالة هو جميع الأعداد الحقيقية.القسم 5. الاتفاقيات.
في المستقبل، عند النظر في أمثلة حل المعادلات، سيتم استخدام الاتفاقيات التالية: ( - علامة النظام [ - علامة المجمل عند حل نظام المعادلات (عدم المساواة)، يتم العثور على تقاطع حلول المعادلات (عدم المساواة) المدرجة في النظام. عند حل مجموعة من المعادلات (المتباينات) يتم إيجاد اتحاد الحلول المتضمنة في مجموعة المعادلات (المتباينات).الفصل 2. حل المعادلات التي تحتوي على معامل.
سنتناول في هذا الفصل الطرق الجبرية لحل المعادلات التي تحتوي على وحدة واحدة أو أكثر.القسم 1. معادلات النموذج │F (x)│= م
تسمى المعادلة من هذا النوع بالأبسط. لها حل إذا وفقط إذا كانت m ≥ 0. حسب تعريف المعامل، فإن المعادلة الأصلية تعادل مجموعة من معادلتين: │ F(خ)│=م
أمثلة:
№1. حل المعادلة: │7x - 2│= 9
الجواب: × 1
= - 1؛ X 2
= 1
4
/
7
№2
│x 2 + 3x + 1│= 1
س 2 + 3س + 2 = 0 × 2 +3x = 0 × 1 = -1؛ س 2 = -2 س (س + 3) = 0 × 1 = 0؛ × 2 = -3 الجواب: مجموع الجذور هو -2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 تشير إلى x 2 = m, m ≥ 0 x = 0 ; ±√5 م 2 - 5 م + 4 = 0 م = 1؛ 4 – كلتا القيمتين تحققان الشرط m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 الجواب: عدد جذور المعادلة 7. التمارين:
№1. حل المعادلة وحدد مجموع الجذور: │x - 5│= 3 №2 . حل المعادلة وحدد الجذر الأصغر: │x 2 + x│= 0 №3 . حل المعادلة وحدد الجذر الأكبر: │x 2 - 5x + 4│= 4 №4 حل المعادلة وحدد الجذر الكامل: │2x 2 – 7x + 6│= 1 №5 حل المعادلة وحدد عدد الجذور: │x 4 – 13x 2 + 50│= 14
القسم 2. معادلات النموذج F(│×│) = م
وسيطة الدالة على الجانب الأيسر تقع تحت علامة المعامل، والجانب الأيمن مستقل عن المتغير. دعونا نفكر في طريقتين لحل المعادلات من هذا النوع. 1 الطريق:من خلال تعريف القيمة المطلقة، فإن المعادلة الأصلية تعادل الجمع بين نظامين. في كل منها يتم فرض شرط على تعبير فرعي. F(│x│) =م
بما أن الدالة F(│x│) زوجية في مجال التعريف بأكمله، فإن جذور المعادلتين F(x) = m وF(- x) = m هي أزواج من الأرقام المتضادة. ولذلك يكفي حل أحد الأنظمة (عند النظر في الأمثلة بهذه الطريقة، سيتم إعطاء الحل لنظام واحد). الطريقة الثانية:تطبيق طريقة إدخال متغير جديد. في هذه الحالة، يتم تقديم التعيين │x│= a، حيث ≥ 0. هذه الطريقة أقل ضخامة في التصميم. أمثلة: №1 . حل المعادلة: 3x 2 - 4│x│= - 1 لنستخدم إدخال متغير جديد. دعونا نشير إلى │x│= a، حيث a ≥ 0. نحصل على المعادلة 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 ارجع إلى المتغير الأصلي: │ س│=1 و │×│= 1/3. كل معادلة لها جذرين. الجواب: × 1 = 1؛ X 2 = - 1؛ X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. حل المعادلة: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x2
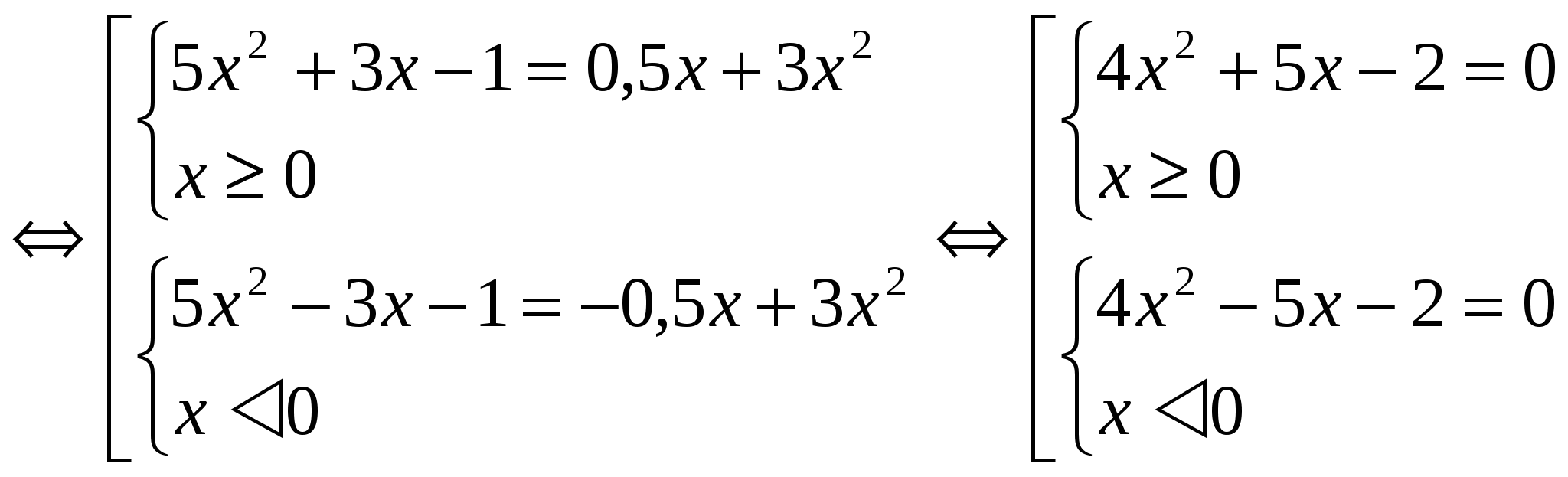لنجد حل النظام الأول للسكان: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 لاحظ أن x 2 غير كافية الشرط x ≥ 0. الحل النظام الثاني سيكون الرقم المقابل للقيمة x 1. الجواب: × 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
حل المعادلة: x 4 – │x│= 0 نشير إلى │x│= a، حيث a ≥ 0. نحصل على المعادلة a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 ارجع إلى المتغير الأصلي: │x│=0 و │x│= 1 x = 0; ± 1 الجواب: × 1
= 0؛ X 2
= 1؛ X 3
= - 1.
التمارين: №6. حل المعادلة: 2│×│ - 4.5 = 5 – 3 / 8 │×│ №7 . حل المعادلة، حدد عدد الجذور في إجابتك: 3x 2 - 7│x│ + 2 = 0 №8 . حل المعادلة، وحدد الحلول الصحيحة في إجابتك: x 4 + │x│ - 2 = 0
القسم 3. معادلات النموذج │F(x)│ = G(x)
يعتمد الجانب الأيمن من معادلة من هذا النوع على متغير، وبالتالي، يكون له حل إذا وفقط إذا كان الطرف الأيمن عبارة عن دالة G(x) ≥ 0. يمكن حل المعادلة الأصلية بطريقتين : 1 الطريق:المعيار، يعتمد على الكشف عن الوحدة بناءً على تعريفها ويتكون من انتقال مكافئ إلى مزيج من نظامين. │ F(خ) │ =ز(X)
يمكن استخدام هذه الطريقة بطريقة عقلانية في حالة التعبير المعقد للدالة G(x) والتعبير الأقل تعقيدًا للدالة F(x)، لأنه من المفترض أن يتم حل عدم المساواة مع الدالة F(x). الطريقة الثانية:يتكون من الانتقال إلى نظام مكافئ يتم فيه فرض شرط على الجانب الأيمن. │ F(س)│=
ز(س)
تكون هذه الطريقة أكثر ملاءمة للاستخدام إذا كان تعبير الدالة G(x) أقل تعقيدًا من الدالة F(x)، حيث يُفترض حل المتباينة G(x) ≥ 0. بالإضافة إلى ذلك، في الحالة من عدة وحدات، فمن المستحسن استخدام الخيار الثاني. أمثلة:
№1.
حل المعادلة: │x + 2│= 6 -2x 
(1 الطريق) الجواب: س = 1 1
/
3
№2.
│x 2 - 2x - 1│= 2·(س + 1)
(طريقتان) الجواب: حاصل ضرب الجذور هو 3.№3. حل المعادلة وحدد مجموع الجذور في إجابتك:
│x - 6│= x 2 - 5x + 9
الجواب: مجموع الجذور هو 4.
التمارين: №9. │x + 4│= - 3x №10. حل المعادلة، حدد عدد الحلول في إجابتك:│x 2 + x - 1│= 2x - 1 №11 . حل المعادلة، وحدد حاصل ضرب الجذور في إجابتك:│x + 3│= x 2 + x – 6
القسم 4. معادلات النموذج │F(x)│= F(x) و │F(x)│= - F(x)
تسمى المعادلات من هذا النوع أحيانًا "الأجمل". بما أن الجانب الأيمن من المعادلات يعتمد على المتغير، فإن الحلول موجودة فقط إذا كان الطرف الأيمن غير سالب. وبالتالي فإن المعادلات الأصلية تعادل المتباينات:│F(x)│= F(x) F(x) ≥ 0 و │F(x)│= - F(x) F(x) أمثلة: №1 . حل المعادلة، وحدد الجذر الصحيح الأصغر في إجابتك: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0.6 الجواب: س = 1№2. حل المعادلة، وضح طول الفاصل الزمني في إجابتك: │x 2 - 9│= 9 – x 2 x 2 – 9 ≥ 0 (x – 3) (x + 3) ≥ 0 [- 3; 3] الجواب: طول الفاصل هو 6.№3 . حل المعادلة وحدد عدد الحلول الصحيحة في إجابتك: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≥ 0 [- 1; 2] الجواب: 4 حلول كاملة.№4 . حل المعادلة وحدد الجذر الأكبر في إجابتك:
│4 - س -
│= 4 – س – 
س 2 – 5س + 5 = 0 د = 5 × 1.2 = 
≈ 1,4الجواب: س = 3.
التمارين:
№12.
حل المعادلة، حدد الجذر بالكامل في إجابتك: │x 2 + 6x + 8│= x 2 + 6x + 8 №13.
حل المعادلة، حدد عدد الحلول الصحيحة في إجابتك: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14.
حل المعادلة؛ في إجابتك، أشر إلى عدد صحيح ليس جذر المعادلة: 
القسم 5. معادلات النموذج │F(x)│= │G(x)│
بما أن طرفي المعادلة غير سالبين، فإن الحل يتضمن النظر في حالتين: التعبيرات الجزئية متساوية أو معاكسة في الإشارة. ولذلك، فإن المعادلة الأصلية تعادل الجمع بين معادلتين: │ F(س)│= │ ز(س)│
أمثلة:
№1.
حل المعادلة، حدد الجذر بالكامل في إجابتك: │x + 3│=│2x - 1│ 
الجواب: الجذر الكامل س = 4.№2.
حل المعادلة: │
س – س 2 – 1│=│2س – 3 – س 2 │ 
الجواب: س = 2.№3
.
حل المعادلة وحدد حاصل ضرب الجذور في إجابتك: 
المعادلات الجذرية 4x 2 + 2x – 1 = 0 x 1.2 = - 1±√5 / 4 الجواب: حاصل ضرب الجذور هو 0.25. التمارين:
№15
. حل المعادلة وحدد الحل الكامل في إجابتك: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
حل المعادلة، حدد الجذر الأصغر في إجابتك:│5x - 3│=│7 - x│ №17
. حل المعادلة وحدد مجموع الجذور في إجابتك: 
القسم 6. أمثلة على حل المعادلات غير القياسية
في هذا القسم سنلقي نظرة على أمثلة للمعادلات غير القياسية، عند حلها يتم الكشف عن القيمة المطلقة للتعبير عن طريق التعريف. أمثلة:№1.
حل المعادلة، وضح مجموع الجذور في إجابتك: x · │x│- 5x – 6 = 0 
الجواب: مجموع الجذور هو 1 №2.
.
حل المعادلة، وحدد الجذر الأصغر في إجابتك: x 2 - 4x · 
- 5 = 0 
الإجابة: الجذر الأصغر x = - 5. №3.
حل المعادلة: 
الجواب: س = -1. التمارين:
№18.
حل المعادلة وحدد مجموع الجذور: x · │3x + 5│= 3x 2 + 4x + 3
№19.
حل المعادلة: × 2 – 3س = 
№20.
حل المعادلة: 
القسم 7. معادلات النموذج │F(x)│+│G(x)│=0
من السهل ملاحظة أنه على الجانب الأيسر من المعادلة من هذا النوع يوجد مجموع الكميات غير السالبة. لذلك، يكون للمعادلة الأصلية حل إذا وفقط إذا كان كلا الحدين يساوي صفرًا في نفس الوقت. المعادلة تعادل نظام المعادلات: │ F(س)│+│ ز(س)│=0
أمثلة:
№1
. حل المعادلة: 
الجواب: س = 2. №2.
حل المعادلة: الجواب: س = 1. التمارين:
№21.
حل المعادلة: №22
. حل المعادلة وحدد مجموع الجذور في إجابتك: №23
. حل المعادلة وحدد عدد الحلول في إجابتك: القسم 8. معادلات النموذج │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m
لحل المعادلات من هذا النوع، يتم استخدام طريقة الفاصل. إذا قمنا بحلها عن طريق التوسع المتسلسل للوحدات، فسنحصل على نمجموعات من الأنظمة، وهي مرهقة للغاية وغير مريحة. دعونا نفكر في خوارزمية طريقة الفاصل الزمني: 1). البحث عن القيم المتغيرة X، حيث تساوي كل وحدة صفرًا (أصفار التعبيرات الفرعية):
2). قم بتمييز القيم التي تم العثور عليها على خط الأعداد، وهو مقسم إلى فترات (عدد الفواصل الزمنية يساوي على التوالي ن+1
) 3). تحديد العلامة التي يتم الكشف عن كل وحدة في كل من الفواصل الزمنية التي تم الحصول عليها (عند إجراء حل، يمكنك استخدام خط الأعداد، بمناسبة العلامات الموجودة عليه) 4). المعادلة الأصلية تعادل المجموع ن+1
الأنظمة التي يشار في كل منها إلى عضوية المتغير Xواحدة من الفواصل. أمثلة:
№1
. حل المعادلة وحدد الجذر الأكبر في إجابتك: 
1). دعونا نجد أصفار التعبيرات الجزئية: x = 2; س = -3 2). دعونا نضع علامة على القيم التي تم العثور عليها على خط الأعداد ونحدد العلامة التي تظهر بها كل وحدة على الفواصل الزمنية الناتجة: س – 2 س – 2 س – 2 – - + - 3 2 × 2س + 6 2س + 6 2س + 6 - + + 3)
- لا يوجد حلول المعادلة لها جذرين. الجواب: الجذر الأكبر س = 2. №2.
حل المعادلة وقدم الجذر الكامل في إجابتك: 
1). دعونا نجد أصفار التعبيرات الجزئية: x = 1.5; س = - 1 2). دعونا نضع علامة على القيم التي تم العثور عليها على خط الأعداد ونحدد العلامة التي تظهر بها كل وحدة على الفواصل الزمنية الناتجة: x + 1 x + 1 x + 1 - + + -1 1.5 × 2س – 3 2س – 3 2س – 3 - - +
3).
النظام الأخير ليس له حلول، وبالتالي فإن المعادلة لها جذرين. عند حل المعادلة، يجب الانتباه إلى علامة "-" الموجودة أمام الوحدة الثانية. الجواب: الجذر الكامل س = 7. №3.
حل المعادلة، وضح مجموع الجذور في إجابتك: 1). دعونا نجد أصفار التعبيرات الجزئية: x = 5; س = 1؛ س = - 2 2). دعونا نضع علامة على القيم التي تم العثور عليها على خط الأعداد ونحدد العلامة التي تظهر بها كل وحدة على الفواصل الزمنية الناتجة: x – 5 x – 5 x – 5 x – 5 - - - + -2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
المعادلة لها جذرين x = 0 و 2. الجواب: مجموع الجذور هو 2. №4
.
حل المعادلة: 1). دعونا نجد أصفار التعبيرات الجزئية: x = 1; س = 2؛ س = 3. 2). دعونا نحدد العلامة التي تظهر بها كل وحدة على الفواصل الزمنية الناتجة. 3). 
دعونا نجمع بين حلول الأنظمة الثلاثة الأولى. إجابة: ؛ س = 5.التمارين: №24. حل المعادلة:
№25.
حل المعادلة وحدد مجموع الجذور في إجابتك: №26.
حل المعادلة وحدد الجذر الأصغر في إجابتك: №27.
حل المعادلة وحدد الجذر الأكبر في إجابتك: القسم 9. المعادلات التي تحتوي على عدة وحدات
تفترض المعادلات التي تحتوي على وحدات متعددة وجود قيم مطلقة في التعبيرات الجزئية. المبدأ الأساسي لحل المعادلات من هذا النوع هو الكشف المتسلسل للوحدات، بدءًا من الوحدة "الخارجية". أثناء الحل، يتم استخدام التقنيات التي تمت مناقشتها في الأقسام رقم 1، رقم 3.أمثلة:
№1.
حل المعادلة: 
الجواب: س = 1؛ - أحد عشر. №2.
حل المعادلة:
الجواب: س = 0؛ 4؛ - 4. №3.
حل المعادلة وحدد حاصل ضرب الجذور في إجابتك: 
الجواب: حاصل ضرب الجذور هو 8. №4.
حل المعادلة: 
دعونا نشير إلى معادلات السكان (1)
و (2)
ودراسة الحل لكل واحد منهم على حدة لسهولة التصميم. وبما أن كلتا المعادلتين تحتويان على أكثر من وحدة واحدة، فمن الملائم أكثر إجراء انتقال مكافئ إلى مجموعات من الأنظمة. (1)
(2)
إجابة:
التمارين:
№36.
حل المعادلة، وضح مجموع الجذور في إجابتك: 5 │3x-5│ = 25 x №37.
حل المعادلة، إذا كان هناك أكثر من جذر، وضح مجموع الجذور في إجابتك: │x + 2│ x – 3x – 10 = 1 №38.
حل المعادلة: 3 │2x -4│ = 9 │x│ №39.
حل المعادلة وحدد عدد الجذور في إجابتك: 2 │ sin x│ = √2 №40
. حل المعادلة وحدد عدد الجذور في إجابتك:
القسم 3. المعادلات اللوغاريتمية.
قبل حل المعادلات التالية لا بد من مراجعة خصائص اللوغاريتمات والدالة اللوغاريتمية. أمثلة: №1. حل المعادلة، وحدد حاصل ضرب الجذور في إجابتك: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. س+1≠0 س≠ - 1الحالة 1: إذا كانت x ≥ - 1، فإن log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – يفي بالشرط x ≥ - 1 2 الحالة: إذا x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 سجل 2 (-(x+1) 3) = سجل 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – يفي بالشرط x - 1
الجواب: حاصل ضرب الجذور هو 15.
№2.
حل المعادلة، وضح مجموع الجذور في إجابتك: lg 
O.D.Z. 
الجواب: مجموع الجذور هو 0.5.
№3.
حل المعادلة: سجل 5 
O.D.Z. 
الجواب: س = 9. №4.
حل المعادلة: │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 لنستخدم الصيغة للانتقال إلى قاعدة أخرى. │2 - سجل 5 س│+ 3 = │1 + سجل 5 س│
│2 - log 5 x│- │1 + log 5 x│= - 3 لنجد أصفار التعبيرات الجزئية: x = 25; x = تقسم هذه الأرقام نطاق القيم المقبولة إلى ثلاث فترات، وبالتالي فإن المعادلة تعادل مجموعة من ثلاثة أنظمة. 
إجابة: )
