Используя преобразования выражений простейшие методы интегрирования. Методы интегрирования

4.1. ПРОСТЕЙШИЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 4.1.1. Понятие неопределенного интеграла

В дифференциальном исчислении рассматривалась задача нахождения производной или дифференциала по заданной функции y = F(x), т. е. необходимо было найти f (x) = F"(x) или dF(x) = F"(x) dx = f (x) dx. Поставим обратную задачу: восстановить продифференцированную функцию, т. е., зная производную f(x) (или дифференциал f(x)dx), найти такую функцию F(x), чтобы F"(x) = f (x). Эта задача оказывается значительно более трудной, чем задача дифференцирования. Например, пусть известна скорость перемещения точки, а надо найти закон

ее перемещения S = S(t), причемДля решения подобных

задач вводятся новые понятия и действия.

Определение. Дифференцируемая функция F(x) называется первообразной для функции f (x) на (a; b), если F"(x) = f (x) на (a; b).

Например, для f (x) = x 2 первообразная так как

для f (x) = cos x первообразной будет F(x) = sin x, потому что F"(x) = (sin x)" = cos x, что совпадает с f (x).

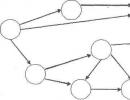
Всегда ли существует первообразная для заданной функции f (x)? Да, если эта функция непрерывна на (a; b). Кроме того, первообразных бесчисленное множество, и отличаются они друг от друга только постоянным слагаемым. Действительно, sin x + 2, sin x - 2, sin x + c - все эти функции будут первообразными для cos x (производная от постоянной величины равна 0) - рис. 4.1.

Определение. Выражение F(x) + C, где С - произвольная постоянная величина, определяющее множество первообразных для функции f (x), называется неопределенным интегралом и обозначается символом , т. е., где знак - знак неопределенного

интеграла, f (x) - называется подынтегральной функцией, f (x)dx - подынтегральньм выражением, х - переменной интегрирования.

Рис. 4.1. Пример семейства интегральных кривых

Определение. Операция нахождения первообразной по заданной производной или дифференциалу называется интегрированием этой функции.

Интегрирование - действие, обратное дифференцированию, его можно проверить дифференцированием, причем дифференцирование однозначно, а интегрирование дает ответ с точностью до постоянной. Придавая постоянной величине С конкретные значенияпо-

лучим различные функции

каждая из которых задает на координатной плоскости кривую, называемую интегральной. Все графики интегральных кривых сдвинуты параллельно относительно друг друга вдоль оси Oy. Следовательно, геометрически неопределенный интеграл представляет собой семейство интегральных кривых.

Итак, введены новые понятия (первообразной и неопределенного интеграла) и новое действие (интегрирование), но как все-таки находить первообразную? Чтобы легко было ответить на этот вопрос, надо в первую очередь составить и выучить наизусть таблицу неопределенных интегралов от основных элементарных функций. Она получается в результате обращения соответствующих формул дифференцирования. Например, если

Обычно в таблицу включаются некоторые интегралы, полученные после применения простейших методов интегрирования. Эти формулы помечены в табл. 4.1 символом «*» и доказаны при дальнейшем изложении материала.

Таблица 4.1. Таблица основных неопределенных интегралов

Формула 11 из табл. 4.1 может иметь вид
,

так как. Аналогичное замечание и по поводу фор-

мулы 13:

4.1.2. Свойства неопределенных интегралов

Рассмотрим простейшие свойства неопределенного интеграла, которые позволят интегрировать не только основные элементарные функции.

1.Производная от неопределенного интеграла равна подынтегральной функции:

2.Дифференциал от неопределенного интеграла равен подынтегральному выражению:

3.Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной:

Пример 1. Пример 2.

4.Постоянный множитель можно выносить за знак интеграла: Пример 3.

5.Интеграл от суммы или разности двух функций равен сумме или разности интегралов от этих функций:

Пример 4.

Формула интегрирования остается справедливой, если переменная интегрирования является функцией: если то

Произвольная функция, имеющая непрерывную производную. Это свойство называется инвариантностью.

Пример 5., поэтому

Сравнить с

Универсального способа интегрирования не существует. Далее будут приведены некоторые методы, позволяющие вычислить заданный интеграл с помощью свойств 1-5 и табл. 4.1.

4.1.3.Непосредственное интегрирование

Этот метод заключается в прямом использовании табличных интегралов и свойств 4 и 5. Примеры.

4.1.4.Метод разложения

Этот метод заключается в разложении подынтегральной функции в линейную комбинацию функций с уже известными интегралами.

Примеры.

4.1.5. Метод подведения под знак дифференциала

Для приведения данного интеграла к табличному бывает удобно сделать преобразования дифференциала.

1. Подведение под знак дифференциала линейной функции

отсюда
в частности, dx = d(x + b),

дифференциал не меняется, если к переменной прибавить

или отнять постоянную величину. Если переменная увеличивается в несколько раз, то дифференциал умножается на обратную величину. Примеры с решениями.

Проверим формулы 9*, 12* и 14* из табл. 4.1, используя метод подведения под знак дифференциала:

что и требовалось доказать.

2. Подведение под знак дифференциала основных элементарных функций:

Замечание. Формулы 15* и 16* могут быть проверены дифференцированием (см. свойство 1). Например,

а это и есть подынтегральная функция из формулы 16*.

4.1.6. Метод выделения полного квадрата из квадратичного трехчлена

При интегрировании выражений типа или

выделением полного квадрата из квадратного трехчлена

ax 2 + bx + c удается свести их к табличным 12*, 14*, 15* или 16* (см. табл. 4.1).

Поскольку в общем виде эта операция выглядит сложнее, чем на самом деле, ограничимся примерами.

Примеры.

Решение. Здесь мы выделяем полный квадрат из квадратного трехчлена x 2 + 6x + 9 = (x 2 + 6x + 9) - 9 + 5 = (x + 3) 2 - 4 , а затем используем метод подведения под знак дифференциала.

Рассуждая аналогично, можно вычислить следующие интегралы:

2. 3.

На заключительном этапе интегрирования была использована формула 16*.

4.1.7. Основные методы интегрирования

Таких методов два: метод замены переменной, или подстановка, и интегрирование по частям.

Метод замены переменной

Существуют две формулы замены переменной в неопределенном интеграле:

1) 2)

Здесьсуть монотонные дифференцируемые функ-

ции своих переменных.

Искусство применения метода состоит, в основном, в выборе функцийтак, чтобы новые интегралы являлись табличными или сводились к ним. В окончательном ответе следует вернуться к старой переменной.

Заметим, что подведение под знак дифференциала является частным случаем замены переменной.

Примеры.

Решение. Здесь следует ввести новую переменную t так, чтобы избавиться от квадратного корня. Положим x + 1 = t, тогда x = t 2 + 1, а dx = 2 tdt:

Решение. Заменив x - 2 на t, получим в знаменателе одночлен и после почленного деления интеграл сведется к табличному от степенной функции:

При переходе к переменной x использованы формулы:

Метод интегрирования по частям

Дифференциал произведения двух функций определяется формулой

Интегрируя это равенство (см. свойство 3), найдем:

ОтсюдаЭто и есть формула интегрирования по

частям.

Интегрирование по частям предполагает субъективное представление подынтегрального выражения в виде u . dV, и при этом интеграл должен быть проще, чемВ противном случае применение

метода не имеет смысла.

Итак, метод интегрирования по частям предполагает умение выделять из подынтегрального выражения сомножители u и dV с учетом вышеизложенных требований.

Приведем ряд типичных интегралов, которые могут быть найдены методом интегрирования по частям. 1. Интегралы вида

где P(x) - многочлен; k - постоянная. В этом случае u = P(x), а dV - все остальные сомножители.

Пример 1.

2.Интегралы типа

Здесь положим- другие сомножители.

Пример 2.

Пример 3.
Пример 4.

Любой результат можно проверить дифференцированием. Напр мер, в данном случае

Результат верен.

3.Интегралы вида

где a, b - const. За u следует взять e ax , sin bx или cos bx.

Пример 5.

Отсюда получаем Пример 6.

Отсюда

Пример 7.
Пример 8.

Решение. Здесь надо сперва сделать замену переменной, а потом интегрировать по частям:

Пример 9.
Пример 10.

Решение. Этот интеграл с равным успехом может быть найден как в результате замены переменной 1 + х 2 = t 2 , так и методом интегрирования по частям:

Самостоятельная работа

Выполнить непосредственное интегрирование (1-10).

Применить простейшие методы интегрирования (11-46).

Выполнить интегрирование, используя методы замены переменной и интегрирования по частям (47-74).

Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x ∈X справедливо равенство:

F " (x) = f(x). (8.1)

Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -

Если F(x) - какая-нибудь первобразная для функции f(x), то ∫ f(x)dx = F(x) + C, (8.2)

где С- произвольная постоянная.

Таблица интегралов

Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:

1) d∫f(x)dx=f(x)

2)∫df(x)=f(x)+C

3) ∫af(x)dx=a∫f(x)dx (a=const)

4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx

Список табличных интегралов

1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)

3.∫a x dx = a x /ln a + C (a>0, a ≠1)

4.∫e x dx = e x + C

5.∫sin x dx = cosx + C

6.∫cos x dx = - sin x + C

7. = arctg x + C

8. = arcsin x + C

10. = - ctg x + C

Замена переменной

Для интегрирования многих функций применяют метод замены переменной или подстановки, позволяющий приводить интегралы к табличной форме.

Если функция f(z) непрерывна на [α,β], функция z =g(x) имеет на непрерывную производную и α ≤ g(x) ≤ β, то

∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)

причем после интегрирования в правой части следует сделать подстановку z=g(x).

Для доказательства достаточно записать исходный интеграл в виде:

∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).

Например:

Метод интегрирования по частям

Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные . Тогда, по произведения,

d(uv))= udv + vdu или udv = d(uv) - vdu.

Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:

∫ udv = uv - ∫ vdu (8.4.)

Эта формула выражает правило интегрирования по частям . Оно приводит интегрирование выражения udv=uv"dx к интегрированию выражения vdu=vu"dx.

Пусть, например, требуется найти ∫xcosx dx. Положим u = x, dv = cosxdx, так что du=dx, v=sinx. Тогда

∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.

Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,

∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и другие, которые вычисляются именно с помощью интегрирования по частям.

Определенный интеграл

Понятие определенного интеграла вводится следующим образом. Пусть на отрезке определена функция f(x). Разобьем отрезок [ a,b] на n частей точками a= x 0 < x 1 <...< x n = b. Из каждого интервала (x i-1 , x i) возьмем произвольную точку ξ i и составим сумму f(ξ i) Δx i где
Δ x i =x i - x i-1 . Сумма вида f(ξ i)Δ x i называется интегральной суммой , а ее предел при λ = maxΔx i → 0, если он существует и конечен, называется определенным интегралом функции f(x) от a до b и обозначается:

F(ξ i)Δx i (8.5).

Функция f(x) в этом случае называется интегрируемой на отрезке , числа a и b носят название нижнего и верхнего предела интеграла .

Для определенного интеграла справедливы следующие свойства:

4), (k = const, k∈R);

7) f(ξ)(b-a) (ξ∈).

Последнее свойство называется теоремой о среднем значении .

Пусть f(x) непрерывна на . Тогда на этом отрезке существует неопределенный интеграл

∫f(x)dx = F(x) + C

и имеет место формула Ньютона-Лейбница , cвязывающая определенный интеграл с неопределенным:

F(b) - F(a). (8.6)

Геометрическая интерпретация: определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), прямыми x = a и x = b и отрезком оси Ox .

Несобственные интегралы

Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:

(8.7)

Если этот предел существует и конечен, то называется сходящимся несобственным интегралом от f(x) на интервале [а,+ ∞), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+ ∞). В противном случае про интеграл говорят, что он не существует или расходится .

Аналогично определяются несобственные интегралы на интервалах (-∞,b] и (-∞, + ∞):

Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка , кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:

если эти пределы существуют и конечны. Обозначение:

Примеры вычисления интегралов

Пример 3.30. Вычислить ∫dx/(x+2).

Решение. Обозначим t = x+2, тогда dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| + C .

Пример 3.31 . Найти ∫ tgxdx.

Решение. ∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Пусть t=cosx, тогда ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.

Пример 3.32 . Найти ∫dx/sinx

Решение.

Пример 3.33. Найти .

Решение. = .

Пример 3.34 . Найти ∫arctgxdx.

Решение. Интегрируем по частям. Обозначим u=arctgx, dv=dx. Тогда du = dx/(x 2 +1), v=x, откуда ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; так как
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Пример 3.35 . Вычислить ∫lnxdx.

Решение. Применяя формулу интегрирования по частям, получим:
u=lnx, dv=dx, du=1/x dx, v=x. Тогда ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.

Пример 3.36 . Вычислить ∫e x sinxdx.

Решение. Обозначим u = e x , dv = sinxdx, тогда du = e x dx, v =∫sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Интеграл ∫e x cosxdx также интегрируем по частям: u = e x , dv = cosxdx, du=e x dx, v=sinx. Имеем:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Получили соотношение ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, откуда 2∫e x sinx dx = - e x cosx + e x sinx + С.

Пример 3.37. Вычислить J = ∫cos(lnx)dx/x.

Решение. Так как dx/x = dlnx, то J= ∫cos(lnx)d(lnx). Заменяя lnx через t, приходим к табличному интегралу J = ∫ costdt = sint + C = sin(lnx) + C.

Пример 3.38 . Вычислить J = .

Решение. Учитывая, что = d(lnx), производим подстановку lnx = t. Тогда J = .

Пример 3.39 . Вычислить интеграл J = .

Решение. Имеем: . Поэтому =
=
=. вводится так sqrt(tan(x/2)).

А если в окне результата нажмете на Show steps в правом верхнем углу, то получите подробное решение.

Интегральное исчисление.

Первообразная функция.

Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке , если в любой точке этого отрезка верно равенство:

Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.

F 1 (x) = F 2 (x) + C.

Неопределенный интеграл.

Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:

Записывают:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Свойства:

Пример:

Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.

Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.

Интеграл	Значение	Интеграл	Значение

	lnsinx+ C



	ln

Методы интегрирования.

Рассмотрим три основных метода интегрирования.

Непосредственное интегрирование.

Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.

Рассмотрим применение этого метода на примере:

Требуется найти значение интеграла . На основе известной формулы дифференцирования
можно сделать вывод, что искомый интеграл равен
, где С – некоторое постоянное число. Однако, с другой стороны
. Таким образом, окончательно можно сделать вывод:

Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.

Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.

Способ подстановки (замены переменных).

Теорема: Если требуется найти интеграл
, но сложно отыскать первообразную, то с помощью замены x = (t) и dx = (t)dt получается:

Доказательство : Продифференцируем предлагаемое равенство:

По рассмотренному выше свойству №2 неопределенного интеграла:

f (x ) dx = f [  (t )]  (t ) dt

что с учетом введенных обозначений и является исходным предположением. Теорема доказана.

Пример. Найти неопределенный интеграл
.

Сделаем замену t = sinx , dt = cosxdt .

Пример.

Замена
Получаем:

Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.

Интегрирование по частям.

Способ основан на известной формуле производной произведения:

(uv) = uv + vu

где u и v – некоторые функции от х.

В дифференциальной форме: d(uv) = udv + vdu

Проинтегрировав, получаем:
, а в соответствии с приведенными выше свойствами неопределенного интеграла:

или
;

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

Пример.

Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.

Пример.

Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.

Таким образом, интеграл найден вообще без применения таблиц интегралов.

Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.

Пример.

Интегрирование элементарных дробей.

Определение: Элементарными называются дроби следующих четырех типов:

I.
III.

II.
IV.

m, n – натуральные числа (m  2, n  2) и b 2 – 4ac <0.

Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.

Рассмотрим метод интегрирования элементарных дробей вида III.

Интеграл дроби вида III может быть представлен в виде:

Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.

Рассмотрим применение указанной выше формулы на примерах.

Пример.

Вообще говоря, если у трехчлена ax 2 + bx + c выражение b 2 – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.

Пример .

Пример.

Рассмотрим теперь методы интегрирования простейших дробей IV типа.

Сначала рассмотрим частный случай при М = 0, N = 1.

Тогда интеграл вида
можно путем выделения в знаменателе полного квадрата представить в виде
. Сделаем следующее преобразование:

Второй интеграл, входящий в это равенство, будем брать по частям.

Обозначим:

Для исходного интеграла получаем:

Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл
.

Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.

В полученном равенстве первый интеграл с помощью подстановки t = u 2 + s приводится к табличному , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.

Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n , а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.

Пример :

Интегрирование рациональных функций.

Интегрирование рациональных дробей.

Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.

Теорема: Если
- правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P (x ) = (x - a )  …(x - b )  (x 2 + px + q )  …(x 2 + rx + s )  ), то эта дробь может быть разложена на элементарные по следующей схеме:

где A i , B i , M i , N i , R i , S i – некоторые постоянные величины.

При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин A i , B i , M i , N i , R i , S i применяют так называемый метод неопределенных коэффициентов , суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.

Применение этого метода рассмотрим на конкретном примере.

Пример.

Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:

Пример.

Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:

6x 5 – 8x 4 – 25x 3 + 20x 2 – 76x – 7 3x 3 – 4x 2 – 17x + 6

6x 5 – 8x 4 – 34x 3 + 12x 2 2x 2 + 3

9x 3 + 8x 2 – 76x - 7

9x 3 – 12x 2 – 51x +18

20x 2 – 25x – 25

Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:

3x 3 – 4x 2 – 17x + 6 x - 3

3x 3 – 9x 2 3x 2 + 5x - 2

Таким образом 3x 3 – 4x 2 – 17x + 6 = (x – 3)(3x 2 + 5x – 2) = (x – 3)(x + 2)(3x – 1). Тогда:

Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений . Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:

Окончательно получаем:

Пример.

Найдем неопределенные коэффициенты:

Тогда значение заданного интеграла:

Интегрирование некоторых тригонометрических

функций.

Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.

Интеграл вида
.

Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.

Интегралы этого вида вычисляются с помощью подстановки
. Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.

Тогда

Таким образом:

Описанное выше преобразование называется универсальной тригонометрической подстановкой.

Пример.

Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.

Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.

Пример.

Интеграл вида
если

функция R cosx .

Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx .

Функция
может содержать cosx только в четных степенях, а, следовательно, может быть преобразована в рациональную функцию относительно sinx.

Пример.

Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.

Интеграл вида
если

функция R является нечетной относительно sinx .

По аналогии с рассмотренным выше случаем делается подстановка t = cosx .

Пример.

Интеграл вида

функция R четная относительно sinx и cosx .

Для преобразования функции R в рациональную используется подстановка

t = tgx.

Пример.

Интеграл произведения синусов и косинусов

различных аргументов.

В зависимости от типа произведения применятся одна из трех формул:

Пример.

Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.

Пример.

Иногда применяются некоторые нестандартные приемы.

Пример.

Интегрирование некоторых иррациональных функций.

Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.

Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.

Интеграл вида
где n - натуральное число.

С помощью подстановки
функция рационализируется.

Пример.

Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.

Проиллюстрируем это на примере.

Пример.

Интегрирование биноминальных дифференциалов.

Определение . Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или подынтегрального выражения) и применяя свойства неопределенного интеграла приводится к одному или нескольким табличным интегралам называется непосредственным интегрированием .

Часто при непосредственном интегрировании используются следующие преобразования дифференциала (операция «внесения под знак дифференциала»):

Например . 1) ;

При вычислении данных интегралов пользовались формулами 1 и 2 таблицы интегралов, которая приведена ниже.

Таблица основных неопределенных интегралов.

Метод интегрирования подстановкой (заменой переменной).

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования. При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.

Данный метод интегрирования основывается на следующей теореме:

Теорема. Пусть функцию f(x) можно представить в виде: f(x)=g(j(x))×j¢(х), тогда если G(u) является первообразной для g(u), то и G(j(x)) является первообразной для g(j(x)). То есть имеет место равенство: .

Например.

Метод интегрирования по частям.

Интегрирование по частям состоит в том, что подынтегральное выражение некоторого интеграла представляется в виде произведения двух сомножителей u и dv, затем используется формула интегрирования по частям.

Теорема Пусть функции u(x) и v(x) дифференцируемы, тогда имеет место формула:

Так как u¢(x)dx=du, v¢(x)dx=dv, то формулу можно переписать в виде:

Например.

Формулу интегрирования по частям в процессе решения можно применять несколько раз.

Например

перенесем из правой части равенства в левую:

Некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям:

; ; , где Р(х)– многочлен от х, к – некоторое число	u=P(x), dv – остальные множители
; ; ; ;	dv=P(x)dх, u – все остальные множители
; , где а и b – некоторые числа	, dv – остальные множители

Интегрирование рациональных дробей.

ОпределениеРациональными будем называть дроби вида , где P n (x), Q m (x) многочлены соответственно n-ой и m-ой степени от х. К простейшим рациональным дробям отнесем дроби четырех типов:

Где А и а – некоторые действительные числа, – простейшая дробь первого типа;

– простейшая дробь второго типа;

– простейшая дробь третьего типа;

– простейшая дробь четвертого типа.

Рассмотрим интегрирование дробей первых трех типов.

3) Интегрирование простейшей дроби третьего типа проводится в два этапа. Разберем процесс интегрирования на примере.

(выделим в числителе производную знаменателя для последующего внесения под знак дифференциала: (х 2 +2х+3)¢=2х+2)

Определение Рациональные дроби называются правильными если степень многочлена в числителе меньше степени многочлена в знаменателе и неправильными если степень многочлена в числителе больше или равна степени многочлена в знаменателе.

В случае неправильной рациональной дроби возможно выделить целую часть. Для этого многочлен из числителя делят с остатком на многочлен знаменателя. Полученное частное будет целой частью, а остаток – числителем новой правильной рациональной дроби. Например, выделим целую часть: .

Таким образом, интегрирование рациональных дробей в обоих случаях сводится к интегрированию правильной рациональной дроби, которая не всегда является простейшей рациональной дробью одного из четырех типов.

Рассмотрим некоторый многочлен Q(x). Пусть число а является корнем этого многочлена, тогда Q(x)=(х-а)Q 1 (x), где Q 1 (x) – многочлен степени на 1 меньше степени Q(x). Число а может быть корнем кратности к, тогда Q(x)=(х-а) к Q 2 (x), где Q 2 (x) – многочлен степени на к меньше степени Q(x). Кроме того, многочлен Q(x) наряду с действительными корнями может иметь комплексный корень a+bi, тогда комплексное число a-bi также будет корнем Q(x). В этом случае Q(x)=(х 2 +px+q)Q 3 (x), где х 2 +px+q=(х-(a+bi))(х-(a-bi)). Если же указанные комплексные числа являются корнями кратности m, тогда Q(x)=(х 2 +px+q) m Q 4 (x).

Таким образом, всякий многочлен Q(x) можно представить в виде:

Q(x)=(х-а 1) к 1 (х-а 2) к 2 …(х-а n) k n (х 2 +p 1 x+q 1) m 1 (х 2 +p 2 x+q 2) m 2 …(х 2 +p s x+q s) m s .

Теорема. Любую правильную рациональную дробь можно представить в виде суммы простейших рациональных дробей 1-4 типов.

Например. Рассмотрим алгоритм представления правильной рациональной дроби в виде суммы простейших рациональных дробей 1-4 типов.

Так как знаменатели дробей равны, очевидно, должны быть равны и числители, а это равенство возможно при равенстве коэффициентов при одинаковых степенях х. Таким образом, подставив вместо неопределенных коэффициентов A, B, C их значения получим: .

Например Найти интеграл .

Подынтегральная функция является неправильной рациональной дробью. После деления числителя на знаменатель с остатком получим: .

Разложим правильную рациональную дробь на простейшие методом неопределенных коэффициентов:

Отсюда следует, что Решая полученную систему линейных уравнений, получаем Тогда , то есть = ;

Найдем отдельно

Таким образом, .

Интегрирование тригонометрических функций.

1. Пусть необходимо найти , где R – некоторая функция

При отыскании таких интегралов часто бывает полезно воспользоваться универсальной тригонометрической подстановкой: . С ее помощью всегда можно перейти от интеграла тригонометрической функции к интегралу от рациональной функции:

Х=2arctgt, .

2. Если функция R(sinx, cosx) нечетна относительно sinx, то есть R(-sinx, cosx)=- R(sinx, cosx), то применяют подстановку cosx=t;

3. Если функция R(sinx, cosx) нечетна относительно соsx, то есть R(sinx, -cosx)=- R(sinx, cosx), то применяют подстановку sinx=t;

4. Если функция R(sinx, cosx) четна относительно sinx и соsx, то есть R(-sinx, -cosx)=R(sinx, cosx), то применяют подстановку tgx=t; такая же подстановка применяется в случае .

Например.

Например Найти интеграл . Подынтегральная функция четна относительно sinx, тогда применяем подстановку tgx=t.

5. Для нахождения интегралов вида используют следующие приемы:

а) если n – нечетное целое положительное число, то используют подстановку sinx=t;

б) если m – нечетное целое положительное число, то используют подстановку соsx=t;

в) если m и n – целые неотрицательные четные числа, то используют формулы понижения порядка ; ; ;

г) если m+n – четное отрицательное целое число, то используют подстановку tgx=t.

Например. .

Например. . ; приводятся к интегралам от тригонометрических функций с помощью следующих подстановок:

а) для интеграла подстановка х=a×sint;

б) для интеграла подстановка х=a×tgt;

в) для интеграла подстановка .

Вычислить первообразные функции мы можем не всегда, но задача на дифференцирование может быть решена для любой функции. Именно поэтому единого метода интегрирования, который можно использовать для любых типов вычислений, не существует.

В рамках данного материала мы разберем примеры решения задач, связанных с нахождением неопределенного интеграла, и посмотрим, для каких типов подынтегральных функций подойдет каждый метод.

Yandex.RTB R-A-339285-1

Метод непосредственного интегрирования

Основной метод вычисления первообразной функции – это непосредственное интегрирование. Это действие основано на свойствах неопределенного интеграла, и для вычислений нам понадобится таблица первообразных. Прочие методы могут лишь помочь привести исходный интеграл к табличному виду.

Пример 1

Вычислите множество первообразных функции f (x) = 2 x + 3 2 · 5 x + 4 3 .

Решение

Для начала изменим вид функции на f (x) = 2 x + 3 2 · 5 x + 4 3 = 2 x + 3 2 · 5 x + 4 1 3 .

Мы знаем, что интеграл суммы функций будет равен сумме этих интегралов, значит:

∫ f (x) d x = ∫ 3 2 · 5 x + 4 3 = 2 x + 3 2 · 5 x + 4 1 3 d x = ∫ 3 2 · 5 x + 4 1 3 d x

Выводим за знак интеграла числовой коэффициент:

∫ f (x) d x = ∫ 2 x d x + ∫ 3 2 (5 x + 4) 1 3 d x = = ∫ 2 x d x + 2 3 · ∫ (5 x + 4) 1 3 d x

Чтобы найти первый интеграл, нам нужно будет обратиться к таблице первообразных. Берем из нее значение ∫ 2 x d x = 2 x ln 2 + C 1

Чтобы найти второй интеграл, потребуется таблица первообразных для степенной функции ∫ x p · d x = x p + 1 p + 1 + C , а также правило ∫ f k · x + b d x = 1 k · F (k · x + b) + C .

Следовательно, ∫ f (x) d x = ∫ 2 x d x + 3 2 · ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 · 3 20 · (5 x + 4) 4 3 + C 2 = = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C

У нас получилось следующее:

∫ f (x) d x = ∫ 2 x d x + 3 2 · ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 · 3 20 · (5 x + 4) 4 3 + C 2 = = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C

причем C = C 1 + 3 2 C 2

Ответ: ∫ f (x) d x = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C

Непосредственному интегрированию с применением таблиц первообразных мы посвятили отдельную статью. Рекомендуем вам ознакомиться с ней.

Метод подстановки

Такой метод интегрирования заключается в выражении подынтегральной функции через новую переменную, введенную специально для этой цели. В итоге мы должны получить табличный вид интеграла или просто менее сложный интеграл.

Этот метод очень полезен, когда нужно интегрировать функции с радикалами или тригонометрические функции.

Пример 2

Вычислите неопределенный интеграл ∫ 1 x 2 x - 9 d x .

Решение

Добавим еще одну переменную z = 2 x - 9 . Теперь нам нужно выразить x через z:

z 2 = 2 x - 9 ⇒ x = z 2 + 9 2 ⇒ d x = d z 2 + 9 2 = z 2 + 9 2 " d z = 1 2 · z d z = z d z

∫ d x x 2 x - 9 = ∫ z d z z 2 + 9 2 · z = 2 ∫ d z z 2 + 9

Берем таблицу первообразных и узнаем, что 2 ∫ d z z 2 + 9 = 2 3 a r c t g z 3 + C .

Теперь нам нужно вернуться к переменной x и получить ответ:

2 3 a r c t g z 3 + C = 2 3 a r c t g 2 x - 9 3 + C

Ответ: ∫ 1 x 2 x - 9 d x = 2 3 a r c t g 2 x - 9 3 + C .

Если нам приходится интегрировать функции с иррациональностью вида x m (a + b x n) p , где значения m , n , p являются рациональными числами, то важно правильно составить выражение для введения новой переменной. Подробнее об этом читайте в статье, посвященной интегрированию иррациональных функций.

Как мы говорили выше, метод подстановки удобно использовать, когда требуется интегрировать тригонометрическую функцию. Например, с помощью универсальной подстановки можно привести выражение к дробно рациональному виду.

Это метод объясняет правило интегрирования ∫ f (k · x + b) d x = 1 k · F (k · x + b) + C .

Добавляем еще одну переменную z = k · x + b . У нас получается следующее:

x = z k - b k ⇒ d x = d z k - b k = z k - b k " d z = d z k

Теперь берем получившиеся выражения и добавляем их в интеграл, заданный в условии:

∫ f (k · x + b) d x = ∫ f (z) · d z k = 1 k · ∫ f (z) d z = = 1 k · F z + C 1 = F (z) k + C 1 k

Если же мы примем C 1 k = C и вернемся к исходной переменной x , то у нас получится:

F (z) k + C 1 k = 1 k · F k x + b + C

Метод подведения под знак дифференциала

Это метод основывается на преобразовании подынтегрального выражения в функцию вида f (g (x)) d (g (x)) . После этого мы выполняем подстановку, вводя новую переменную z = g (x) , находим для нее первообразную и возвращаемся к исходной переменной.

∫ f (g (x)) d (g (x)) = g (x) = z = ∫ f (z) d (z) = = F (z) + C = z = g (x) = F (g (x)) + C

Чтобы быстрее решать задачи с использованием этого метода, держите под рукой таблицу производных в виде дифференциалов и таблицу первообразных, чтобы найти выражение, к которому надо будет приводится подынтегральное выражение.

Разберем задачу, в которой нужно вычислить множество первообразных функции котангенса.

Пример 3

Вычислите неопределенный интеграл ∫ c t g x d x .

Решение

Преобразуем исходное выражение под интегралом с помощью основных тригонометрических формул.

c t g x d x = cos s d x sin x

Смотрим в таблицу производных и видим, что числитель можно подвести под знак дифференциала cos x · d x = d (sin x) , значит:

c t g x d x = cos x d x sin x = d sin x sin x , т.е. ∫ c t g x d x = ∫ d sin x sin x .

Допустим, что sin x = z , в таком случае ∫ d sin x sin x = ∫ d z z . Согласно таблице первообразных, ∫ d z z = ln z + C . Теперь вернемся к исходной переменной ∫ d z z = ln z + C = ln sin x + C .

Все решение в кратком виде можно записать так:

∫ с t g x d x = ∫ cos x d x sin x = ∫ d sin x sin x = s i n x = t = = ∫ d t t = ln t + C = t = sin x = ln sin x + C

Ответ: ∫ с t g x d x = ln sin x + C

Метод подведения под знак дифференциала очень часто используется на практике, поэтому советуем вам прочесть отдельную статью, посвященную ему.

Метод интегрирования по частям

Этот метод основывается на преобразовании подынтегрального выражения в произведение вида f (x) d x = u (x) · v " x d x = u (x) · d (v (x)) , после чего применяется формула ∫ u (x) · d (v (x)) = u (x) · v (x) - ∫ v (x) · d u (x) . Это очень удобный и распространенный метод решения. Иногда частичное интегрирование в одной задаче приходится применять несколько раз до получения нужного результата.

Разберем задачу, в которой нужно вычислить множество первообразных арктангенса.

Пример 4

Вычислите неопределенный интеграл ∫ a r c t g (2 x) d x .

Решение

Допустим, что u (x) = a r c t g (2 x) , d (v (x)) = d x , в таком случае:

d (u (x)) = u " (x) d x = a r c t g (2 x) " d x = 2 d x 1 + 4 x 2 v (x) = ∫ d (v (x)) = ∫ d x = x

Когда мы вычисляем значение функции v (x) , прибавлять постоянную произвольную С не следует.

∫ a r c t g (2 x) d x = u (x) · v (x) - ∫ v (x) d (u (x)) = = x · a r c t g (2 x) - ∫ 2 x d x 1 + 4 x 2

Получившийся интеграл вычисляем, используя метод подведения под знак дифференциала.

Поскольку ∫ a r c t g (2 x) d x = u (x) · v (x) - ∫ v (x) d (u (x)) = x · a r c t g (2 x) - ∫ 2 x d x 1 + 4 x 2 , тогда 2 x d x = 1 4 d (1 + 4 x 2) .

∫ a r c t g (2 x) d x = x · a r c t g (2 x) - ∫ 2 x d x 1 + 4 x 2 = = x · a r c t g (2 x) - 1 4 ln 1 + 4 x 2 + C 1 = = x · a r c t g (2 x) - 1 4 ln 1 + 4 x 2 + C

Ответ: ∫ a r c t g (2 x) d x = x · a r c t g (2 x) - 1 4 ln 1 + 4 x 2 + C .

Главная сложность применения такого метода – это необходимость выбирать, какую часть брать за дифференциал, а какую – за функцию u (x) . В статье, посвященной методу интегрирования по частям, даны некоторые советы по этому вопросу, с которыми следует ознакомиться.

Если нам требуется найти множество первообразных дробно рациональной функции, то нужно сначала представить подынтегральную функцию в виде суммы простейших дробей, а потом интегрировать получившиеся дроби. Подробнее см. статью об интегрировании простейших дробей.

Если мы интегрируем степенное выражение вида sin 7 x · d x или d x (x 2 + a 2) 8 , то нам будут полезны рекуррентные формулы, которые могут постепенно понижать степень. Они выводятся с помощью последовательного многократного интегрирования по частям. Советуем прочитать статью «Интегрирование с помощью рекуррентных формул.

Подведем итоги. Для решения задач очень важно знать метод непосредственного интегрирования. Другие методы (подведение под знак дифференциала, подстановка, интегрирование по частям) также позволяют упростить интеграл и привести его к табличному виду.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

$mob_info$