تذبذبات نظام المفترس والفريسة (نموذج لوتكا-فولتير). الدورات الدراسية: بحث نوعي لنموذج المفترس والفريسة. النموذج الرياضي لنظام الفريسة والمفترس
نماذج التفاعل من نوعين
فرضيات فولتيرا. التشابه مع الحركية الكيميائية. نماذج فولتيرا للتفاعلات. تصنيف أنواع التفاعلات المنافسة. فريسة المفترس. نماذج معممة للتفاعلات بين الأنواع . نموذج كولموجوروف. نموذج ماك آرثر للتفاعل بين نوعين من الحشرات. حدودي وصور طورية لنظام بازيكين.
يعتبر مؤسس النظرية الرياضية الحديثة للسكان بحق هو عالم الرياضيات الإيطالي فيتو فولتيرا، الذي طور النظرية الرياضية للمجتمعات البيولوجية، التي يكون جهازها عبارة عن معادلات تفاضلية وتفاضلية تكاملية.(فيتو فولتيرا. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. باريس، 1931). وفي العقود اللاحقة، تطورت الديناميكيات السكانية بشكل أساسي بما يتماشى مع الأفكار الواردة في هذا الكتاب. نُشرت الترجمة الروسية لكتاب فولتيرا عام 1976 تحت عنوان: "النظرية الرياضية للصراع من أجل الوجود" مع خاتمة بقلم يو.م. سفيريزيف، الذي يدرس تاريخ تطور البيئة الرياضية في الفترة 1931-1976.
كتاب فولتيرا مكتوب بنفس الطريقة التي تكتب بها كتب الرياضيات. يقوم أولاً بصياغة بعض الافتراضات حول الأشياء الرياضية التي من المفترض دراستها، ومن ثم إجراء دراسة رياضية لخصائص هذه الأشياء.
تتكون الأنظمة التي درسها فولتيرا من نوعين أو أكثر. وفي بعض الحالات، يتم أخذ إمدادات الأغذية المستخدمة بعين الاعتبار. تعتمد المعادلات التي تصف تفاعل هذه الأنواع على المفاهيم التالية.
فرضيات فولتيرا
1. يكون الطعام إما متوفرًا بكميات غير محدودة، أو يتم تنظيم إمداده بشكل صارم مع مرور الوقت.
2. يموت الأفراد من كل نوع بطريقة تؤدي إلى موت نسبة ثابتة من الأفراد الموجودين في كل وحدة زمنية.
3. الأنواع المفترسة تأكل الضحايا، وفي كل وحدة زمنية يتناسب دائمًا عدد الضحايا المأكولين مع احتمال الالتقاء بأفراد من هذين النوعين، أي. نتاج عدد الحيوانات المفترسة وعدد الفرائس.
4. إذا كان هناك غذاء بكميات محدودة والعديد من الأنواع القادرة على استهلاكه، فإن حصة الغذاء التي يستهلكها نوع ما في وحدة زمنية تتناسب مع عدد أفراد هذا النوع، مأخوذة بمعامل معين يعتمد على عدد أفراد هذا النوع. الأنواع (نماذج المنافسة بين الأنواع).
5. إذا كان أحد الأنواع يتغذى على غذاء متوفر بكميات غير محدودة فإن الزيادة في عدد الأنواع في وحدة الزمن تتناسب مع عدد الأنواع.
6. إذا كان نوع ما يتغذى على الغذاء المتوفر بكميات محدودة، فإن تكاثره ينظمه معدل استهلاك الغذاء، أي تكاثره. وفي كل وحدة زمنية، تتناسب الزيادة مع كمية الطعام الذي يتم تناوله.
التشابه مع الحركية الكيميائية
هذه الفرضيات لها أوجه تشابه وثيقة مع الحركية الكيميائية. وفي معادلات الديناميكا السكانية، كما في معادلات الحركية الكيميائية، يستخدم "مبدأ التصادم"، عندما يتناسب معدل التفاعل مع حاصل ضرب تراكيز المكونات المتفاعلة.
في الواقع، وفقًا لفرضيات فولتيرا، فإن السرعةعملية يتناسب انقراض كل نوع مع عدد الأنواع. في الحركية الكيميائية، يتوافق ذلك مع تفاعل أحادي الجزيئي لتحلل مادة معينة، وفي النموذج الرياضي، يتوافق مع الحدود الخطية السالبة على الجانب الأيمن من المعادلات.
وفقا لمفاهيم الحركية الكيميائية، فإن معدل التفاعل الجزيئي للتفاعل بين مادتين يتناسب مع احتمال تصادم هاتين المادتين، أي: نتاج تركيزهم. وبنفس الطريقة، ووفقاً لفرضيات فولتيرا، فإن معدل تكاثر الحيوانات المفترسة (موت الفريسة) يتناسب مع احتمال اللقاءات بين الأفراد المفترسة والفريسة، أي. نتاج أعدادهم. في كلتا الحالتين، تظهر الحدود الثنائية في النظام النموذجي على الجانب الأيمن من المعادلات المقابلة.
وأخيرًا، فإن الحدود الإيجابية الخطية الموجودة على الجانب الأيمن من معادلات فولتيرا، والتي تتوافق مع نمو السكان في ظل ظروف غير محدودة، تتوافق مع شروط التحفيز الذاتي التفاعلات الكيميائية. يتيح لنا هذا التشابه في المعادلات في النماذج الكيميائية والبيئية تطبيق نفس أساليب البحث في النمذجة الرياضية للحركية السكانية كما هو الحال في أنظمة التفاعلات الكيميائية.
تصنيف أنواع التفاعلات
وفقا لفرضيات فولتيرا، فإن التفاعل بين نوعين، أعدادهما س 1 و س 2 يمكن وصفها بالمعادلات:
(9.1)
هنا المعلمات أ أنا - ثوابت معدل نمو النوع، ج أنا- ثوابت التحديد الذاتي للأعداد (المنافسة بين الأنواع) ، ب ي- ثوابت تفاعل الأنواع، (أنا, ي= 1،2). تحدد علامات هذه المعاملات نوع التفاعل.
في الأدبيات البيولوجية، يتم تصنيف التفاعلات عادةً وفقًا للآليات المعنية. التنوع هنا هائل: تفاعلات غذائية متنوعة، وتفاعلات كيميائية بين البكتيريا والطحالب العوالق، وتفاعلات الفطريات مع الكائنات الحية الأخرى، وتعاقب الكائنات النباتية، المرتبطة بشكل خاص بالتنافس على ضوء الشمسومع تطور التربة، وما إلى ذلك. وهذا التصنيف يبدو واسعا.
ه . Odum، مع الأخذ في الاعتبار النماذج التي اقترحها V. Volterra، اقترح التصنيف ليس من خلال الآليات، ولكن من خلال النتائج. وفقًا لهذا التصنيف، ينبغي تقييم العلاقات على أنها إيجابية أو سلبية أو محايدة اعتمادًا على ما إذا كانت وفرة أحد الأنواع تزيد أو تتناقص أو تظل دون تغيير في وجود نوع آخر. ثم يمكن عرض الأنواع الرئيسية للتفاعلات في شكل جدول.
أنواع تفاعل الأنواع
|
تكافل |
ب 12 ,ب 21 >0 |
||
|
معايشة |
ب 12 ,>0, ب 21 =0 |
||
|
المفترس الضحية |
ب 12 ,>0, ب 21 <0 |
||
|
الأمنسالية |
ب 12 ,=0, ب 21 <0 |
||
|
مسابقة |
ب 12 , ب 21 <0 |
||
|
الحياد |
ب 12 , ب 21 =0 |
العمود الأخير يوضح علامات معاملات التفاعل من النظام (9.1)
دعونا نلقي نظرة على الأنواع الرئيسية للتفاعلات
معادلات المنافسة:
وكما رأينا في المحاضرة السادسة فإن معادلات المنافسة هي:
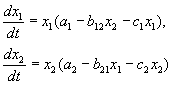 (9.2)
(9.2)
حلول الأنظمة الثابتة:
(1).
![]()
أصل الإحداثيات، لأي معلمات النظام، هو عقدة غير مستقرة.
(2).
![]() (9.3)
(9.3)
ج الحالة الثابتة (9.3) هي سرج عند أ 1 > ب 12 /مع 2 و
عقدة مستقرة في أ 1 12 /ق 2 . ويعني هذا الشرط أن النوع ينقرض إذا كان معدل نموه أقل من قيمة حرجة معينة.
(3).
![]() (9.4)
(9.4)
ج الحل الثابت (9.4)¾ سرج عند أ 2 > ب 21 /ج 1 وعقدة مستقرة في أ 2< ب 21 /ج 1
(4).
![]() (9.5)
(9.5)
تميز الحالة الثابتة (9.5) التعايش بين نوعين متنافسين وتمثل عقدة مستقرة إذا تم استيفاء العلاقة:
![]()
وهذا يعني عدم المساواة:
ب 12
ب 21
مما يسمح لنا بصياغة شرط التعايش بين الأنواع:
منتج معاملات التفاعل بين السكان أقل من منتج معاملات التفاعل السكاني.
وبالفعل، فلتكن معدلات النمو الطبيعي للنوعين قيد النظرأ 1 ، أ 2 هي نفسها. عندها سيكون الشرط الضروري للاستقرار
ج 2 > ب 12 ، ج 1 > ب 21 .
تظهر هذه التفاوتات أن الزيادة في حجم أحد المنافسين تؤدي إلى قمع نموه أكثر من نمو منافس آخر. إذا كانت أعداد كلا النوعين محدودة، جزئيًا أو كليًا، بموارد مختلفة، فإن عدم المساواة المذكورة أعلاه صحيحة. إذا كان لدى كلا النوعين نفس الاحتياجات تمامًا، فسيكون أحدهما أكثر قابلية للحياة وسيحل محل منافسه.
إن سلوك مسارات طور النظام يعطي فكرة واضحة عن النتائج المحتملة للمنافسة. دعونا نساوي الأطراف اليمنى من معادلات النظام (9.2) بالصفر:
س 1 (أ 1 – ج 1 س 1 – ب 12 س 2) = 0 (dx 1 /دينار = 0),
س 2 (أ 2 –ب 21 س 1 – ج 2 س 2) = 0 (dx 2 /دينار = 0),
في هذه الحالة، نحصل على معادلات للخطوط المتساوية الرئيسية للنظام
س 2= – ب21 س 1 / ج 2 +أ 2 /ج 2، س 2 = 0
- معادلات الخطوط المتساوية للمماسات الرأسية.
س 2= – ج1 س 1 / ب12+ أ 1 /ب 12 , س 1 = 0
- معادلات الخطوط المتساوية للمماسات الرأسية. تمثل نقاط التقاطع الزوجي للخطوط المتساوية لأنظمة الظل الرأسية والأفقية حلولاً ثابتة لنظام المعادلات (9.2.) وإحداثياتها ![]() هي أعداد ثابتة من الأنواع المتنافسة.
هي أعداد ثابتة من الأنواع المتنافسة.
يظهر الموقع المحتمل للخطوط المتساوية الرئيسية في النظام (9.2) في الشكل 9.1. أرز. 9.1أيتوافق مع بقاء النوعس 1، الشكل. 9.1 ب- بقاء النوعس 2، الشكل. 9.1 الخامس- تعايش الأنواع عند استيفاء الشرط (9.6). الشكل 9.1زيوضح نظام الزناد. هنا تعتمد نتيجة المنافسة على الظروف الأولية. الحالة الثابتة غير الصفرية (9.5) لكلا النوعين غير مستقرة. وهذا هو السرج الذي يمر من خلاله الفاصل، الذي يفصل بين مناطق البقاء لكل نوع.

أرز. 9.1.موقع الخطوط المتساوية الرئيسية على الصورة الطورية لنظام فولتيرا للمنافسة من نوعين (9.2) بنسب مختلفة من المعلمات. التوضيحات في النص.
لدراسة المنافسة بين الأنواع، تم إجراء التجارب على مجموعة واسعة من الكائنات الحية. عادة، يتم اختيار نوعين مرتبطين ارتباطًا وثيقًا ويتم زراعتهما معًا وبشكل منفصل في ظل ظروف خاضعة لرقابة صارمة. وفي فترات معينة، يتم إجراء تعداد كامل أو انتقائي للسكان. يتم تسجيل وتحليل البيانات من عدة تجارب متكررة. أجريت دراسات على الأوليات (على وجه الخصوص، الهدبيات)، والعديد من أنواع الخنافس من جنس تريبوليوم، ودروسوفيلا، وقشريات المياه العذبة (دافنيا). تم إجراء العديد من التجارب على التجمعات الميكروبية (انظر المحاضرة 11). تم إجراء تجارب أيضًا في الطبيعة، بما في ذلك على المستورقات (رينولدز)، ونوعين من النمل (بونتين)، وما إلى ذلك. 9.2. يصور منحنيات نمو الدياتومات باستخدام نفس المورد (تحتل نفس المكانة البيئية). عندما تزرع في زراعة أحاديةاستريونيللا فورموزا يصل إلى مستوى ثابت من الكثافة ويحافظ على تركيز المورد (السيليكات) عند مستوى منخفض باستمرار. ب. عندما يزرع في زراعة أحاديةسيندراوينا يتصرف بطريقة مماثلة ويحافظ على تركيز السيليكات عند مستوى أقل. ب. أثناء الزراعة المشتركة (في نسختين) Synedrauina يزيح Asterionella formosa. على ما يبدو سيندرا

أرز. 9.2.المنافسة في الدياتومات. أ -عندما تزرع في الزراعة الأحاديةاستريونيللا فورموزا يصل إلى مستوى ثابت من الكثافة ويحافظ على تركيز المورد (السيليكات) عند مستوى منخفض باستمرار. ب -عندما تزرع في الزراعة الأحاديةسيندراوينا يتصرف بطريقة مماثلة ويحافظ على تركيز السيليكات عند مستوى أقل. الخامس -مع الزراعة المشتركة (في نسختين) Synedruina يزيح Asterionella formosa. على ما يبدو سيندرا يفوز بالمنافسة نظرًا لقدرته على الاستفادة الكاملة من الركيزة (انظر أيضًا المحاضرة 11).
إن تجارب دراسة المنافسة التي أجراها جي. جوس معروفة على نطاق واسع، مما يدل على بقاء أحد الأنواع المتنافسة ويسمح له بصياغة "قانون الاستبعاد التنافسي". ينص القانون على أنه يمكن لنوع واحد فقط أن يتواجد في مكان بيئي واحد. في التين. 9.3. يتم عرض نتائج تجارب Gause لنوعين من Parametium، يحتلان نفس المكان البيئي (الشكل 9.3 أ، ب) والأنواع التي تشغل مكانًا بيئيًا مختلفًا (الشكل 9.3 ج).

أرز. 9.3. أ- منحنيات النمو السكاني لنوعينباراميتيوم في المحاصيل ذات النوع الواحد. الدوائر السوداء – P أوريليا، دوائر بيضاء – P. كوداتوم
ب- منحنيات النمو لـ P Aurelia و P . كوداتوم في ثقافة مختلطة.
بقلم جوس، 1934
نموذج المنافسة (9.2) له عيوب، على وجه الخصوص، يترتب على ذلك أن التعايش بين نوعين ممكن فقط إذا كانت أعدادهم محدودة بعوامل مختلفة، ولكن النموذج لا يشير إلى حجم الاختلافات التي يجب أن تكون لضمان التعايش على المدى الطويل . وفي الوقت نفسه، من المعروف أنه من أجل التعايش على المدى الطويل في بيئة متغيرة، من الضروري وجود فرق يصل إلى حجم معين. إن إدخال عناصر عشوائية في النموذج (على سبيل المثال، إدخال وظيفة استخدام الموارد) يسمح لنا بالتحقيق الكمي في هذه المشكلات.
نظام المفترس+الضحية
 (9.7)
(9.7)
وهنا على النقيض من (9.2) العلامات ب 12 و ب 21 مختلفة. كما في حالة المنافسة الأصل
![]() (9.8)
(9.8)
هي نقطة خاصة من نوع العقدة غير المستقرة. ثلاث حالات مستقرة أخرى محتملة:
![]() ,(9.9)
,(9.9)
![]() (9.10)
(9.10)
![]() (9.11)
(9.11)
وبالتالي، من الممكن أن تبقى الفريسة فقط على قيد الحياة (9.10)، فقط المفترس (9.9) (إذا كان لديه مصادر غذائية أخرى) والتعايش بين كلا النوعين (9.11). لقد ناقشنا بالفعل الخيار الأخير في المحاضرة 5. وترد في الشكل 5 الأنواع المحتملة من صور الطور لنظام المفترس والفريسة. 9.4.
Isoclins من الظلال الأفقية هي خطوط مستقيمة
س 2 = – ب 21 X 1 /ج 2 + أ 1/ج 2، X 2 = 0,
وخطوط متساوية من الظلال العمودية- مستقيم
س 2 = - ج 1 X 1 /ب 12 + أ 2 /ب 12 , X 1 = 0.
تقع النقاط الثابتة عند تقاطع الخطوط المتساوية المماسية الرأسية والأفقية.

من الشكل. 9.4 ما يلي مرئيا. نظام المفترس والفريسة (9.7) يمكن أن يكون لها وضع توازن مستقر، حيثس سكان الروم من الضحايا ماتوا تماما ( ) ولم يبق إلا الحيوانات المفترسة (الفترة 2 في الشكل. 9.4 أ). ومن الواضح أن مثل هذا الوضع لا يمكن أن يتحقق إلا إذا، بالإضافة إلى نوع الضحايا المعنيين، X 1 المفترس X 2 – بها مصادر طاقة إضافية . تنعكس هذه الحقيقة في النموذج من خلال الحد الموجب على الجانب الأيمن من المعادلة x2. نقاط خاصة(1) و (3) (الشكل 9.4 أ) غير مستقرة. الاحتمال الثاني – حالة ثابتة مستقرة حيث ينقرض سكان الحيوانات المفترسة تمامًا ولم يبق سوى الفريسة – نقطة مستقرة(3) (الشكل 9.4 6 ). هذه نقطة خاصة (1) – أيضا عقدة غير مستقرة.
وأخيرا الاحتمال الثالث – التعايش المستدام بين الحيوانات المفترسة والفرائس (الشكل 1). 9.4 الخامس) ، يتم التعبير عن أرقامها الثابتة بواسطة الصيغ (9.11).
كما في حالة مجتمع واحد (انظر المحاضرة 3)، بالنسبة للنموذج (9.7) من الممكن تطوير نموذج عشوائي، لكن لا يمكن حله بشكل صريح. ولذلك، فإننا سوف تقتصر على الاعتبارات العامة. لنفترض، على سبيل المثال، أن نقطة التوازن تقع على مسافة معينة من كل محور. ثم لمسارات المرحلة التي القيمس 1 , س 2 تظل كبيرة بما فيه الكفاية، فإن النموذج الحتمي سيكون مرضيا تماما. ولكن إذا لم يكن أي متغير كبيرًا جدًا في مرحلة ما من مسار الطور، فيمكن أن تصبح التقلبات العشوائية كبيرة. وهي تؤدي إلى أن النقطة الممثلة تتحرك إلى أحد المحاور، مما يعني انقراض الأنواع المقابلة لها.
وهكذا، يتبين أن النموذج العشوائي غير مستقر، لأن "الانجراف" العشوائي يؤدي عاجلاً أم آجلاً إلى انقراض أحد الأنواع. في هذا النوع من النماذج، ينقرض الحيوان المفترس في النهاية، إما عن طريق الصدفة أو بسبب القضاء على فرائسه أولاً. يشرح النموذج العشوائي لنظام المفترس والفريسة تجارب غوس جيدًا (غاوس، 1934), فيها الشركات العملاقة باراميتوم كانداتومكان بمثابة ضحية لأهداب آخر ديدينيوم ناساتوم – المفترس. المتوقع وفق المعادلات الحتمية (9.7) كانت أرقام التوازن في هذه التجارب ما يقرب من خمسة أفراد فقط من كل نوع، لذلك ليس من المستغرب أنه في كل تجربة متكررة تموت الحيوانات المفترسة أو الفريسة (وبعدها الحيوانات المفترسة) بسرعة كبيرة. في التين. 9.5.

أرز. 9.5. ارتفاع باراميتيوم كوداتوم والشركات العملاقة المفترسة الدادينيوم ناسوتوم. من : غاوس ج.ف. الصراع من أجل الوجود. بالتيمور, 1934
لذلك، فإن تحليل نماذج فولتيرا للتفاعل بين الأنواع يظهر أنه على الرغم من التنوع الكبير في أنواع سلوك مثل هذه الأنظمة، إلا أنه لا يمكن أن تكون هناك تقلبات غير مقيدة في الأعداد في نموذج الأنواع المتنافسة على الإطلاق. ومع ذلك، لوحظت مثل هذه التذبذبات في الطبيعة وفي التجربة. وكانت الحاجة إلى تفسيرهم النظري أحد أسباب صياغة أوصاف النماذج بشكل أكثر عمومية.
نماذج معممة للتفاعل من نوعين
تم اقتراح عدد كبير من النماذج لوصف التفاعل بين الأنواع، وكان الجانب الأيمن من معادلاتها عبارة عن دالات لأعداد المجموعات السكانية المتفاعلة. تم حل مسألة وضع معايير عامة لتحديد نوع الوظائف التي يمكن أن تصف سلوك حجم السكان المؤقت، بما في ذلك التقلبات المستقرة. أشهر هذه النماذج تعود إلى كولموجوروف (1935، مقال منقح - 1972) وروزنزويج (1963).
 (9.12)
(9.12)
يتضمن النموذج الافتراضات التالية:
1) الحيوانات المفترسة لا تتفاعل مع بعضها البعض، أي. معدل تكاثر المفترس ك 2 وعدد الضحايا ليتم إبادة كل وحدة زمنية بواسطة مفترس واحد لا يعتمد عليه ذ.
2) الزيادة في عدد الفرائس في وجود الحيوانات المفترسة تساوي الزيادة في غياب الحيوانات المفترسة مطروحا منها عدد الفرائس التي أبادتها الحيوانات المفترسة. المهام ك 1 (س), ك 2 (س), ل(س) ، مستمرة ومحددة على شبه المحور الموجب س, ذ³ 0.
3) dk 1 /dx< 0. وهذا يعني أن معدل تكاثر الفرائس في حالة عدم وجود حيوان مفترس يتناقص بشكل رتيب مع زيادة عدد الفرائس، مما يعكس محدودية توافر الغذاء والموارد الأخرى.
4) dk 2 /دكس> 0، ك 2 (0) < 0 < k 2 (¥ ). مع زيادة عدد الفرائس، فإن معامل التكاثر للحيوانات المفترسة يتناقص بشكل رتيب مع زيادة عدد الفرائس، والانتقال من القيم السلبية(عندما لا يكون هناك شيء للأكل) إيجابي.
5) عدد الفرائس التي يدمرها حيوان مفترس واحد في وحدة زمنية ل(س)> 0 في ن> 0; ل(0)=0.
يتم عرض الأنواع المحتملة لصور الطور للنظام (9.12) في الشكل. 9.6:

أرز. 9.6.صور المرحلة لنظام كولموغوروف (9.12)، الذي يصف التفاعل بين نوعين بنسب مختلفة من المعلمات. التوضيحات في النص.
الحلول الثابتة (هناك حلان أو ثلاثة) لها الإحداثيات التالية:
(1). ` س=0;` ص=0.
أصل الإحداثيات لأي قيم معلمات هو السرج (الشكل 9.6 أ-د).
(2). ` س = أ،` ص=0.(9.13)
أتحدد من المعادلة:
ك 1 (أ)=0.
ثابت الحل (9.13) هو السرج إذا ب< أ (الشكل 9.6 أ, ب, ز), ب تحدد من المعادلة
ك 2 (ب)=0
توضع النقطة (9.13) في الربع الموجب إذا ب>أ . هذه عقدة مستقرة .
الحالة الأخيرة، والتي تتوافق مع موت المفترس وبقاء الفريسة، موضحة في الشكل. 9.6 الخامس.
(3). ` س = ب،` ص=ج.(9.14)
يتم تحديد قيمة C من المعادلات:
النقطة (9.14) – التركيز (الشكل 9.6 أ) أو العقدة (الشكل 9.6 ز)، والذي يعتمد استقراره على علامة الكميةس
س 2 = – ك 1 (ب) – ك 1 (ب)ب+ل(ب)ج.
لو س>0, نقطة مستقرة إذاس<0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 ب)
في الأدب الأجنبي، يُنظر في كثير من الأحيان إلى نموذج مماثل اقترحه روزنزويج وماك آرثر (1963):
 (9.15)
(9.15)
أين F(س) - معدل التغير في عدد الضحايا سفي غياب الحيوانات المفترسة، F( س، ص) - شدة الافتراس، ك- المعامل الذي يميز كفاءة معالجة الكتلة الحيوية للفريسة إلى الكتلة الحيوية المفترسة، ه- وفيات الحيوانات المفترسة.
نموذج (9.15) يختزل إلى حالة خاصة من نموذج كولموجوروف (9.12) في ظل الفرضيات التالية:
1) يقتصر عدد الحيوانات المفترسة فقط على عدد الفرائس،
2) السرعة التي يأكل بها حيوان مفترس الفريسة تعتمد فقط على كثافة مجموعة الفريسة ولا تعتمد على كثافة مجموعة الحيوانات المفترسة.
ثم تأخذ المعادلات (9.15) الشكل.

عند وصف التفاعل بين الأنواع الحقيقية، يتم تحديد الأطراف اليمنى من المعادلات وفقًا للأفكار حول الحقائق البيولوجية. دعونا نفكر في أحد النماذج الأكثر شعبية من هذا النوع.
نموذج التفاعل بين نوعين من الحشرات (ماك آرثر، 1971)
تم استخدام النموذج الذي سنتناوله أدناه لحل المشكلة العملية لمكافحة الحشرات الضارة عن طريق تعقيم ذكور أحد الأنواع. وعلى أساس الخصائص البيولوجية لتفاعل الأنواع، تم كتابة النموذج التالي
 (9.16)
(9.16)
هنا س، ص- الكتلة الحيوية لنوعين من الحشرات. التفاعلات الغذائية للأنواع الموصوفة في هذا النموذج معقدة للغاية. هذا يحدد شكل كثيرات الحدود على الجانب الأيمن من المعادلات.
دعونا ننظر إلى الجانب الأيمن من المعادلة الأولى. أنواع الحشرات Xأكل يرقات هذا النوع في(عضو +ك 3 ذ)،ولكن البالغين من هذا النوع فيأكل يرقات هذا النوع Xتخضع لوفرة الأنواع العالية Xأو فيأو كلا النوعين (أعضاء -ك 4 س ص، - ص 2). في صغيرة Xموت الأنواع Xأعلى من زيادته الطبيعية (1 -ك 1 +ك 2 س-س 2 < 0 في صغيرة العاشر).وفي المعادلة الثانية المصطلح ك 5 يعكس النمو الطبيعي للأنواع ذ؛ -ك 6 ذ –ضبط النفس من هذا النوع،-ك 7 س- أكل يرقات هذا النوع فيأنواع الحشرات س، ك 8 xy – زيادة في الكتلة الحيوية للأنواع فيبسبب استهلاك الحشرات البالغة من هذا النوع فييرقات النوع X.
في التين. 9.7 يتم تقديم دورة الحد، وهو مسار الحل الدوري المستقر للنظام (9.16).

لا يمكن بالطبع الحصول على حل لمسألة كيفية ضمان التعايش بين السكان مع بيئتهم البيولوجية دون مراعاة خصوصيات نظام بيولوجي معين وتحليل جميع علاقاته المتبادلة. وفي الوقت نفسه، تسمح لنا دراسة النماذج الرياضية الرسمية بالإجابة على بعض الأسئلة العامة. يمكن القول أنه بالنسبة لنماذج مثل (9.12)، فإن حقيقة التوافق أو عدم التوافق بين المجموعات السكانية لا تعتمد على حجمها الأولي، ولكن يتم تحديدها فقط من خلال طبيعة التفاعل بين الأنواع. يساعد النموذج في الإجابة على السؤال: كيفية التأثير على التكاثر الحيوي وإدارته من أجل تدمير الأنواع الضارة بسرعة.
يمكن اختزال الإدارة إلى تغيير مفاجئ قصير المدى في القيم السكانية Xو ش.تتوافق هذه الطريقة مع طرق التحكم مثل التدمير لمرة واحدة لإحدى المجموعتين أو كلتيهما بالوسائل الكيميائية. من الواضح من البيان المذكور أعلاه أنه بالنسبة للسكان المتوافقين، فإن طريقة التحكم هذه ستكون غير فعالة، لأنه بمرور الوقت سيصل النظام مرة أخرى إلى وضع ثابت.
هناك طريقة أخرى وهي تغيير نوع وظائف التفاعل بين طرق العرض، على سبيل المثال، عند تغيير قيم معلمات النظام. هذه هي الطريقة البارامترية التي تتوافق معها طرق المكافحة البيولوجية. وبالتالي، عند إدخال الذكور المعقمة، ينخفض معدل النمو الطبيعي للسكان. إذا حصلنا في نفس الوقت على نوع مختلف من صورة الطور، حيث لا يوجد سوى حالة ثابتة مستقرة مع عدم وجود أعداد للآفات، فإن التحكم سيؤدي إلى النتيجة المرجوة – تدمير سكان الأنواع الضارة. ومن المثير للاهتمام أن نلاحظ أنه في بعض الأحيان يكون من المستحسن تطبيق التأثير ليس على الآفة نفسها، ولكن على شريكها. بشكل عام، من المستحيل تحديد الطريقة الأكثر فعالية. ويعتمد ذلك على الضوابط المتاحة وعلى الشكل الواضح للوظائف التي تصف التفاعل بين السكان.
نموذج من تصميم أ.د.بازيكين
تم إجراء التحليل النظري لنماذج تفاعلات الأنواع بشكل أكثر شمولاً في كتاب أ.د. بازيكين "الفيزياء الحيوية للتفاعل بين السكان" (M.، Nauka، 1985).
دعونا نفكر في أحد نماذج المفترس والفريسة التي تمت دراستها في هذا الكتاب.
 (9.17)
(9.17)
النظام (9.17) هو تعميم لأبسط نموذج فولتيرا للمفترس والفريسة (5.17) مع الأخذ في الاعتبار تأثير تشبع المفترس. يفترض النموذج (5.17) أن شدة رعي الفرائس تزداد خطياً مع زيادة كثافة الفرائس، وهو ما لا يتوافق مع الواقع عند كثافات الفرائس العالية. يمكن اختيار وظائف مختلفة لوصف اعتماد النظام الغذائي للمفترس على كثافة الفريسة. ومن المهم أن الوظيفة المختارة مع النمو ستميل بشكل مقارب إلى قيمة ثابتة. استخدم نموذج (9.6) الاعتماد اللوجستي. في نموذج بازيكين، يتم اختيار القطع الزائد كدالة س/(1+بكسل). دعونا نتذكر أن هذا هو شكل صيغة مونود، التي تصف اعتماد معدل نمو الكائنات الحية الدقيقة على تركيز الركيزة. هنا تلعب الفريسة دور الركيزة، والمفترس هو دور الكائنات الحية الدقيقة. .
يعتمد النظام (9.17) على سبع معلمات. يمكن تقليل عدد المعلمات عن طريق استبدال المتغيرات:
س® (إعلان)س؛ ذ ® (إعلان)/ص;
ر® (1/أ)ر؛ ز (9.18)
ويعتمد على أربع معلمات.
لإجراء دراسة نوعية كاملة، من الضروري تقسيم مساحة المعلمة رباعية الأبعاد إلى مناطق ذات أنواع مختلفة من السلوك الديناميكي، أي. بناء صورة حدودية أو هيكلية للنظام.
ثم من الضروري إنشاء صور طورية لكل منطقة من مناطق الصورة البارامترية ووصف التشعبات التي تحدث مع صور الطور عند حدود مناطق مختلفة من الصورة البارامترية.
يتم إنشاء صورة حدودية كاملة على شكل مجموعة من "الشرائح" (الإسقاطات) لصورة حدودية منخفضة الأبعاد مع قيم ثابتة لبعض المعلمات.
الصورة البارامترية للنظام (9.18) للثابت زوصغيرة همبين في الشكل 9.8. تحتوي الصورة على 10 مناطق ذات أنواع مختلفة من سلوك مسارات الطور.

أرز. 9.8.الصورة البارامترية للنظام (9.18) للثابتز
وصغيرة ه
يمكن أن يكون سلوك النظام بنسب مختلفة من المعلمات مختلفًا بشكل كبير (الشكل 9.9). يسمح النظام بما يلي:
1) توازن واحد مستقر (المنطقتان 1 و5)؛
2) دورة حدية واحدة مستقرة (المنطقتان 3 و8)؛
3) توازنان مستقران (المنطقة 2)
4) دورة الحد المستقر والتوازن غير المستقر داخلها (المناطق 6، 7، 9، 10)
5) دورة حدية مستقرة وتوازن مستقر خارجها (المنطقة 4).
في المناطق البارامترية 7، 9، 10، تكون منطقة جذب التوازن محدودة بدورة حدودية غير مستقرة تقع داخل دورة مستقرة. الهيكل الأكثر إثارة للاهتمام هو صورة الطور، المقابلة للمنطقة 6 في الصورة البارامترية. يظهر بالتفصيل في الشكل. 9.10.

منطقة جذب التوازن B 2 (المظللة) عبارة عن "حلزون" ملتوي من التركيز غير المستقر B 1. إذا كان من المعروف أنه في اللحظة الأولى من الزمن كان النظام في محيط B 1، فمن الممكن الحكم على ما إذا كان المسار المقابل سيصل إلى التوازن B 2 أو دورة حدية مستقرة تحيط بثلاث نقاط توازن C (السرج)، B 1 و B 2 على أساس الاعتبارات الاحتمالية.

الشكل 9.10.صورة الطور للنظام 9.18 للمنطقة البارامترية 6. منطقة الجذب B2 مظللة
في صورة حدودية(9.7) هناك 22 حدود التشعب المختلفة التي تتشكل 7 أنواع مختلفة من التشعبات. تتيح لنا دراستهم تحديد الأنواع المحتملة لسلوك النظام عندما تتغير معلماته. على سبيل المثال، عند الانتقال من المنطقة 1 إلى المنطقة 3 حدوث ولادة دورة حدية صغيرة، أو ولادة ناعمة للتذبذبات الذاتية حول توازن واحد في.ولادة ناعمة مماثلة للتذبذبات الذاتية، ولكن حول أحد التوازنات، وهي ب 1 , يحدث عند عبور حدود المناطق 2 و 4. عند مغادرة المنطقة 4 إلى المنطقة 5 دورة حدية مستقرة حول نقطة ماب 1 "انفجارات" على حلقة الفواصل وتبقى نقطة الجذب الوحيدة هي التوازن ب 2 إلخ.
من الأمور ذات الأهمية الخاصة للممارسة، بالطبع، تطوير معايير لقرب النظام من حدود التشعب. والواقع أن علماء الأحياء يدركون جيداً خاصية "التخزين المؤقت" أو "المرونة" التي تتمتع بها الأنظمة البيئية الطبيعية. تشير هذه المصطلحات عادةً إلى قدرة النظام على امتصاص التأثيرات الخارجية. وطالما أن شدة التأثير الخارجي لا تتجاوز قيمة حرجة معينة، فإن سلوك النظام لا يخضع لتغييرات نوعية. على مستوى الطور، يتوافق هذا مع عودة النظام إلى حالة التوازن المستقرة أو إلى دورة حدية مستقرة، والتي لا تختلف معلماتها كثيرًا عن تلك الأصلية. عندما تتجاوز شدة التأثير المستوى المسموح به، فإن النظام "ينهار" ويدخل في وضع مختلف نوعيا للسلوك الديناميكي، على سبيل المثال، يموت ببساطة. هذه الظاهرة يتوافق مع انتقال التشعب.
كل نوع من التحولات التشعبية له سماته المميزة، والتي تجعل من الممكن الحكم على خطر مثل هذا التحول على النظام البيئي. فيما يلي بعض المعايير العامة التي تشير إلى قرب الحدود الخطرة. كما هو الحال في أحد الأنواع، عندما يتناقص عدد أحد الأنواع، "يعلق" النظام بالقرب من نقطة سرج غير مستقرة، وهو ما يتم التعبير عنه في استعادة بطيئة للغاية للرقم إلى القيمة الأولية، ثم النظام قريب من الحدود الحرجة. ومن مؤشرات الخطر أيضًا تغير شكل التقلبات في أعداد المفترس والفريسة. إذا أصبحت التذبذبات القريبة من التوافقية تذبذبات استرخاء، وزادت سعة التذبذبات، فقد يؤدي ذلك إلى فقدان استقرار النظام وانقراض أحد الأنواع.
إن المزيد من تعميق النظرية الرياضية للتفاعل بين الأنواع يتماشى مع تفصيل بنية السكان أنفسهم ومراعاة العوامل الزمنية والمكانية.
الأدب.
كولموغوروف أ.ن. دراسة نوعية للنماذج الرياضية للديناميكيات السكانية. // مشاكل علم التحكم الآلي. م، 1972، العدد 5.
MacArtur R. التحليل الرسومي للنظم البيئية // تقرير قسم علم الأحياء بجامعة بيرنسيتون. 1971
AD بازيكين "الفيزياء الحيوية للتفاعل بين السكان." م.، ناوكا، 1985.
فولتيرا: "النظرية الرياضية للصراع من أجل الوجود". م.. العلوم، 1976
جوس ج.ف. الصراع من أجل الوجود. بالتيمور، 1934.
نموذج حاسوبي "الضحية المفترسة"
كازاتشكوف إيجور ألكسيفيتش 1، جوسيفا إيلينا نيكولاييفنا 2
1 جامعة ماجنيتوجورسك التقنية الحكومية سميت باسمها. جي. نوسوفا، معهد البناء والعمارة والفنون، طالبة في السنة الخامسة
2 جامعة ماجنيتوجورسك التقنية الحكومية سميت باسمها. جي. نوسوفا، معهد الطاقة والأنظمة الآلية، مرشح العلوم التربوية، أستاذ مشارك في قسم معلوماتية الأعمال وتكنولوجيا المعلومات
حاشية. ملاحظة
هذه المقالة مخصصة لمحة عامة عن نموذج الكمبيوتر "المفترس والفريسة". تشير الأبحاث التي أجريت إلى أن النمذجة البيئية تلعب دورًا كبيرًا في البحوث البيئية. هذه القضية متعددة الأوجه.
نموذج حاسوبي "الضحية المفترسة"
كازاتشكوف إيجور ألكسيفيتش 1، جوسيفا إيلينا نيكولاييفنا 2
1 جامعة نوسوف ماجنيتوجورسك التقنية الحكومية، معهد الهندسة المدنية والعمارة والفنون، طالب الدورة الخامسة
2 جامعة نوسوف ماجنيتوجورسك التقنية الحكومية، معهد هندسة الطاقة والأنظمة الآلية، دكتوراه في العلوم التربوية، أستاذ مشارك في قسم علوم الكمبيوتر وتكنولوجيا المعلومات التجارية
خلاصة
تقدم هذه المقالة نظرة عامة على نموذج الكمبيوتر "الضحية المفترس". وتشير الدراسة إلى أن المحاكاة البيئية تلعب دورا كبيرا في دراسة البيئة. هذه المشكلة متعددة الأوجه.
يتم استخدام النمذجة البيئية لدراسة بيئتنا. تستخدم النماذج الرياضية في الحالات التي لا توجد فيها بيئة طبيعية ولا كائنات طبيعية، فهي تساعد على التنبؤ بتأثير العوامل المختلفة على الكائن قيد الدراسة. تأخذ هذه الطريقة على عاتقها وظائف فحص وبناء وتفسير النتائج التي تم الحصول عليها. وبناءً على هذه الأشكال، تتعامل النمذجة البيئية مع تقييم التغيرات في البيئة المحيطة بنا.
حاليا، تستخدم مثل هذه النماذج لدراسة البيئة من حولنا، وعندما يكون من الضروري دراسة أي مجال من مجالاتها، يتم استخدام النمذجة الرياضية. يتيح هذا النموذج التنبؤ بتأثير عوامل معينة على موضوع الدراسة. في وقت واحد، تم اقتراح نوع "المفترس والفريسة" من قبل علماء مثل: T. Malthus (Malthus 1798، Malthus 1905)، Verhulst (Verhulst 1838)، Pearl (Pearl 1927، 1930)، وكذلك A. Lotka ( Lotka 1925, 1927 ) و V. Volterra (Volterra 1926). تستنسخ هذه النماذج النظام التذبذبي الدوري الذي ينشأ نتيجة للتفاعلات بين الأنواع في الطبيعة.
إحدى الطرق الرئيسية للمعرفة هي النمذجة. بالإضافة إلى أنه يستطيع التنبؤ بالتغيرات التي تحدث في بيئة، يساعد أيضًا في إيجاد الطريقة المثلى لحل المشكلة. لقد تم استخدام النماذج الرياضية في علم البيئة لفترة طويلة من أجل تحديد الأنماط والاتجاهات في تطور السكان، والمساعدة في تسليط الضوء على جوهر الملاحظات. يمكن أن يكون التخطيط بمثابة عينة سلوك، كائن.
عند إعادة إنشاء الكائنات في علم الأحياء الرياضي، يتم استخدام تنبؤات الأنظمة المختلفة، ويتم توفير خصائص فردية خاصة للأنظمة الحيوية من أجل: الهيكل الداخلي للفرد، وظروف دعم الحياة، وثبات النظم البيئية، والتي بفضلها يتم الحفاظ على النشاط الحيوي للأنظمة .
لقد أدى ظهور النمذجة الحاسوبية إلى تقدم كبير في حدود القدرات البحثية. وقد ظهرت إمكانية التنفيذ المتعدد الأطراف للأشكال الصعبة التي لا تسمح بالدراسة التحليلية، وظهرت اتجاهات جديدة، فضلا عن نمذجة المحاكاة.
دعونا نفكر في ماهية كائن النمذجة. "الجسم عبارة عن موطن مغلق حيث يحدث التفاعل بين مجموعتين بيولوجيتين: الحيوانات المفترسة والفريسة. تحدث عملية النمو والانقراض والتكاثرمباشرة على سطح الموائل. تتغذى الفريسة على الموارد الموجودة في البيئة، بينما تتغذى الحيوانات المفترسة على الفريسة. وفي هذه الحالة، يمكن أن تكون الموارد الغذائية إما متجددة أو غير متجددة.
في عام 1931، استنتج فيتو فولتيرا القوانين التالية للعلاقة بين المفترس والفريسة.
قانون الدورة الدورية - غالبًا ما تؤدي عملية تدمير الفريسة من قبل المفترس إلى تقلبات دورية في حجم السكان لكلا النوعين، اعتمادًا فقط على معدل نمو الحيوانات آكلة اللحوم والحيوانات العاشبة، وعلى النسبة الأولية لأعدادها.
قانون الحفاظ على المتوسطات - متوسط الوفرة لكل نوع ثابت، بغض النظر عن المستوى الأولي، بشرط أن تكون المعدلات المحددة للزيادة السكانية، وكذلك كفاءة الافتراس، ثابتة.
قانون انتهاك القيم المتوسطة - عندما يتم تقليل كلا النوعين بما يتناسب مع عددهما، يزداد متوسط حجم مجتمع الفريسة، ويتناقص حجم الحيوانات المفترسة.
نموذج المفترس والفريسة هو علاقة خاصة بين المفترس وفريسته، ونتيجة لذلك يستفيد كلاهما. الأفراد الأكثر صحة والأكثر تكيفًا مع الظروف البيئية هم الذين يبقون على قيد الحياة، أي. كل هذا يحدث بسبب الانتقاء الطبيعي. في بيئة لا توجد فيها فرصة للتكاثر، سوف يقوم المفترس عاجلاً أم آجلاً بتدمير سكان الفريسة، ونتيجة لذلك سوف ينقرض هو نفسه.
هناك العديد من الكائنات الحية على الأرض التي، في ظل ظروف مواتية، تزيد من عدد أقاربها إلى أبعاد هائلة. وتسمى هذه القدرة: الإمكانات الحيوية للأنواع، أي. زيادة عدد الأنواع خلال فترة زمنية معينة. كل نوع لديه إمكاناته الحيوية الخاصة، على سبيل المثال، الأنواع الكبيرة من الكائنات الحية يمكن أن تتكاثر بنسبة 1.1 مرة فقط في السنة، في حين أن الكائنات الحية من الأنواع الأصغر، مثل القشريات وغيرها. يمكن أن يزيد ظهورها حتى 1030 مرة، والبكتيريا بأعداد أكبر. وفي أي من هذه الحالات، سوف ينمو عدد السكان بشكل كبير.
النمو السكاني الأسي هو تقدم هندسي للنمو السكاني. ويمكن ملاحظة هذه القدرة في المختبر في البكتيريا والخميرة. وفي الظروف غير المخبرية، يمكن ملاحظة النمو الأسي في مثال الجراد أو في أنواع أخرى من الحشرات. يمكن ملاحظة مثل هذه الزيادة في عدد الأنواع في تلك الأماكن التي لا يوجد فيها أي أعداء عملياً، ويوجد فيها ما يكفي من الطعام. وفي نهاية المطاف، حدثت زيادة في الأنواع، وبعد زيادة الأعداد لفترة قصيرة من الزمن، بدأ النمو السكاني في الانخفاض.
دعونا نفكر في نموذج كمبيوتر لتكاثر الثدييات باستخدام نموذج لوتكا-فولتيرا كمثال. يترك في منطقة معينة يعيش نوعان من الحيوانات: الغزلان والذئاب. النموذج الرياضي للتغيرات السكانية في النموذجصواني فولتيرا:
العدد الأولي للضحايا هو xn، وعدد الحيوانات المفترسة هو yn.
معلمات النموذج:
P1 - احتمال لقاء مع حيوان مفترس،
P2 - معامل نمو الحيوانات المفترسة على حساب الفريسة،
د – معدل وفيات الحيوانات المفترسة،
أ – معامل الزيادة في عدد الضحايا.
في المهمة التدريبية تم تحديد القيم التالية: عدد الغزلان 500، عدد الذئاب 10، معدل نمو الغزلان 0.02، معدل نمو الذئاب 0.1، احتمال لقاء حيوان مفترس. 0.0026، وكان معدل نمو الحيوانات المفترسة على حساب الفريسة 0،000056. يتم حساب البيانات لمدة 203 سنة.
نحن نستكشف التأثير معامل الزيادة في الضحايا لتنمية مجموعتين من السكان، سيتم ترك المعلمات المتبقية دون تغيير.في المخطط 1، لوحظت زيادة في عدد الفرائس، وبعد ذلك، مع بعض التأخير، لوحظت زيادة في الحيوانات المفترسة. ثم يقوم الحيوانات المفترسة بضرب الضحايا، وينخفض عدد الضحايا بشكل حاد، وبعد ذلك، ينخفض \u200b\u200bعدد الحيوانات المفترسة (الشكل 1).

الشكل 1. حجم السكان مع انخفاض معدلات المواليد بين الضحايا
دعونا نحلل التغيير في النموذج من خلال زيادة معدل ولادة الضحية a=0.06. في الرسم البياني 2 نرى عملية تذبذبية دورية تؤدي إلى زيادة أعداد كلا المجموعتين مع مرور الوقت (الشكل 2).

الشكل 2. حجم السكان بمتوسط معدل المواليد للضحايا
دعونا نفكر في كيفية تغير الديناميكيات السكانية مع ارتفاع قيمة معدل ولادة الضحية a=1.13. في التين. 3 هناك زيادة حادة في أعداد كلا المجموعتين، يليها انقراض كل من الفرائس والمفترس. ويرجع ذلك إلى حقيقة أن عدد الفرائس قد زاد إلى حد أن الموارد بدأت في النفاد، مما أدى إلى انقراض الفريسة. يحدث انقراض الحيوانات المفترسة بسبب انخفاض عدد الفرائس ونفاد الموارد اللازمة للبقاء على قيد الحياة من الحيوانات المفترسة.

الشكل 3. حجم السكان مع ارتفاع معدلات المواليد بين الضحايا
استنادا إلى تحليل بيانات التجارب الحاسوبية، يمكننا أن نستنتج أن النمذجة الحاسوبية تسمح لنا بالتنبؤ بأحجام السكان ودراسة تأثير العوامل المختلفة على الديناميات السكانية. في المثال أعلاه، قمنا بفحص نموذج المفترس والفريسة، وتأثير معدل ولادة الفرائس على عدد الغزلان والذئاب. تؤدي الزيادة الطفيفة في عدد الفرائس إلى زيادة طفيفة في الفرائس، والتي يتم تدميرها من قبل الحيوانات المفترسة بعد فترة معينة.تؤدي الزيادة المعتدلة في عدد الفرائس إلى زيادة في حجم كلا المجموعتين. تؤدي الزيادة الكبيرة في عدد الفرائس أولاً إلى زيادة سريعة في عدد الفرائس، وهذا يؤثر على زيادة نمو الحيوانات المفترسة، ولكن بعد ذلك تقوم الحيوانات المفترسة المتكاثرة بتدمير أعداد الغزلان بسرعة. ونتيجة لذلك، انقرضت كلا النوعين.
يمكن للحيوانات المفترسة أن تأكل الحيوانات العاشبة وكذلك الحيوانات المفترسة الضعيفة. تمتلك الحيوانات المفترسة مجموعة واسعة من الأطعمة ويمكنها التبديل بسهولة من فريسة إلى أخرى يسهل الوصول إليها. غالبًا ما تهاجم الحيوانات المفترسة الفريسة الضعيفة. يتم الحفاظ على التوازن البيئي بين مجموعات الفرائس المفترسة.[...]
إذا كان التوازن غير مستقر (لا توجد دورات محدودة) أو كانت الدورة الخارجية غير مستقرة، فإن أعداد كلا النوعين، التي تعاني من تقلبات قوية، تترك المنطقة المجاورة للتوازن. علاوة على ذلك، يحدث انحطاط سريع (في الحالة الأولى) مع انخفاض تكيف المفترس، أي. مع ارتفاع معدل الوفيات (مقارنة بمعدل تكاثر الضحية). وهذا يعني أن المفترس الضعيف من جميع النواحي لا يساهم في استقرار النظام ويموت هو نفسه.[...]
يكون ضغط الحيوانات المفترسة قويًا بشكل خاص عندما يتحول التوازن نحو المفترس، في التطور المشترك بين المفترس والفريسة، ويضيق نطاق الفريسة. يرتبط الصراع التنافسي ارتباطًا وثيقًا بنقص الموارد الغذائية؛ ويمكن أن يكون أيضًا صراعًا مباشرًا، على سبيل المثال، بين الحيوانات المفترسة من أجل الفضاء كمورد، ولكنه في أغلب الأحيان يكون مجرد إزاحة نوع لا يملك ما يكفي من الغذاء في مكان ما. منطقة معينة من قبل الأنواع التي لديها ما يكفي من نفس الكمية من الغذاء. هذه بالفعل منافسة بين الأنواع.[...]
 |
وأخيرًا، في نظام "المفترس والفريسة" الذي وصفه النموذج (2.7)، فإن ظهور عدم استقرار الانتشار (مع استقرار التوازن المحلي) لا يكون ممكنًا إلا في حالة زيادة معدل الوفيات الطبيعية للمفترس مع نمو سكانه بشكل أسرع من معدل الوفيات الطبيعية للمفترس. تختلف الوظيفة الخطية والدالة الغذائية عن فولتيرا أو عندما تكون مجموعة الفرائس من نوع أولي.[...]
من الناحية النظرية، في نماذج "مفترس واحد - فريستان"، يمكن للرعي المكافئ (عدم تفضيل نوع أو آخر من أنواع الفرائس) أن يؤثر على التعايش التنافسي لأنواع الفرائس فقط في تلك الأماكن التي يوجد فيها توازن مستقر محتمل بالفعل. لا يمكن أن يزداد التنوع إلا في ظل الظروف التي يكون فيها للأنواع ذات القدرة التنافسية الأقل معدل نمو سكاني أعلى من الأنواع السائدة. وهذا يسمح لنا بفهم الوضع عندما يؤدي الرعي الموحد إلى زيادة تنوع الأنواع النباتية حيث يتعايش عدد أكبر من الأنواع التي تم اختيارها للتكاثر السريع مع الأنواع التي يهدف تطورها إلى زيادة القدرة التنافسية.[...]
وبالمثل، يمكن أن يؤدي اختيار الفرائس المعتمد على الكثافة إلى توازن مستقر في النماذج النظرية لنوعين من الفرائس المتنافسة حيث لم يكن هناك توازن من قبل. للقيام بذلك، يجب أن يكون المفترس قادرًا على تقديم استجابات وظيفية وعددية للتغيرات في كثافة الفريسة؛ ومع ذلك، فمن الممكن أن يكون التبديل (الهجمات المتكررة بشكل غير متناسب على الفرائس الأكثر وفرة) أكثر أهمية. في الواقع، ثبت أن التبديل له تأثير استقرار في أنظمة "مفترس واحد - فريسة" ويمثل الآلية الوحيدة القادرة على تثبيت التفاعلات في الحالات التي تتداخل فيها منافذ الفريسة تمامًا. يمكن للحيوانات المفترسة غير المتخصصة أن تلعب مثل هذا الدور. إن تفضيل الحيوانات المفترسة الأكثر تخصصًا لمنافس مهيمن يعمل بنفس طريقة تبديل الحيوانات المفترسة، ويمكن أن يؤدي إلى تثبيت التفاعلات النظرية في النماذج التي لم يكن هناك في السابق توازن بين أنواع الفرائس، بشرط أن تكون منافذها منفصلة إلى حد ما.[...]
كما أن المفترس "القوي من جميع النواحي" لا يعمل على استقرار المجتمع، أي. تتكيف بشكل جيد مع فريسة معينة مع معدل وفيات نسبي منخفض. في هذه الحالة، يكون للنظام دورة حدية غير مستقرة، وعلى الرغم من استقرار وضع التوازن، فإنه يتدهور في بيئة عشوائية (يأكل المفترس الفريسة ويموت نتيجة لذلك). ويتوافق هذا الوضع مع الانحطاط البطيء.[...]
وبالتالي، مع التكيف الجيد للمفترس في محيط توازن مستقر، يمكن أن تنشأ دورات غير مستقرة ومستقرة، أي. اعتمادًا على الظروف الأولية ، يميل نظام "المفترس والفريسة" إما إلى التوازن ، أو يتأرجح بعيدًا عنه ، أو يتم إنشاء تقلبات مستقرة في أعداد كلا النوعين بالقرب من التوازن. [...]
تتغذى الكائنات الحية التي تصنف على أنها مفترسة على كائنات حية أخرى، مما يؤدي إلى تدمير فرائسها. وبالتالي، بين الكائنات الحية، ينبغي التمييز بين نظام تصنيف آخر، وهي "الحيوانات المفترسة" و "الفريسة". لقد تطورت العلاقات بين هذه الكائنات طوال تطور الحياة على كوكبنا. تعمل الكائنات المفترسة كمنظمين طبيعيين لعدد الكائنات المفترسة. تؤدي زيادة عدد "الفرائس" إلى انخفاض عدد "الفرائس"، وهذا بدوره يقلل من إمداد الغذاء ("الفرائس") لـ "الفرائس"، وهو ما يملي عمومًا انخفاضًا في عددها. من "الفرائس"، وما إلى ذلك. وهكذا، في التكاثر الحيوي، تحدث تقلبات في عدد الحيوانات المفترسة والفرائس باستمرار، ولكن بشكل عام، يتم إنشاء توازن معين لفترة معينة من الزمن ضمن ظروف بيئية مستقرة إلى حد ما.[... ]
ويأتي هذا في نهاية المطاف إلى التوازن البيئي بين الحيوانات المفترسة والفرائس.[...]
بالنسبة للدالة الغذائية من النوع الثالث، ستكون حالة التوازن مستقرة إذا كانت N هي نقطة انعطاف الوظيفة (انظر الشكل 2، ج). وينبع هذا من حقيقة أن الوظيفة الغذائية تكون مقعرة خلال هذه الفترة، وبالتالي، تزداد الحصة النسبية لاستهلاك الفريسة من قبل المفترس.[...]
دع Гг = -Г، أي. هناك مجتمع من نوع "المفترس والفريسة". وفي هذه الحالة يكون الحد الأول في التعبير (7.4) يساوي صفراً، ولتحقيق شرط الثبات من حيث احتمال حالة التوازن N، يشترط ألا يكون الحد الثاني موجباً أيضاً.[.. .]
وبالتالي، بالنسبة لمجتمع المفترس والفريسة، يمكننا أن نستنتج أن موضع التوازن الإيجابي العام مستقر بشكل غير مقارب، أي أنه بالنسبة لأي بيانات أولية 1H(0)>0، يحدث التطور بطريقة N(7) - ■ K بشرط أن N >0.[...]
وهكذا، في بيئة متجانسة لا تحتوي على مأوى للتكاثر، فإن المفترس عاجلا أم آجلا يدمر سكان الفريسة ثم يموت من تلقاء نفسه. موجات الحياة (التغيرات في وفرة المفترس والفريسة) تتبع بعضها البعض مع تحول طور ثابت، وفي المتوسط تظل وفرة كل من المفترس والفريسة عند نفس المستوى تقريبًا. تعتمد مدة الفترة على معدلات نمو كلا النوعين وعلى المعلمات الأولية. بالنسبة لسكان الفرائس، فإن تأثير المفترس إيجابي، لأن تكاثره المفرط سيؤدي إلى انهيار عدد سكانه. وفي المقابل فإن كافة الآليات التي تمنع الإبادة الكاملة للفريسة تساهم في الحفاظ على الإمدادات الغذائية للمفترس.[...]
قد تكون التعديلات الأخرى نتيجة لسلوك المفترس. عدد الفرائس التي يستطيع المفترس أن يستهلكها الوقت المعطى، له حده. يظهر في الجدول تأثير تشبع المفترس عند الاقتراب من هذه العتبة. 2-4، ب. قد يكون للتفاعلات الموصوفة في المعادلتين 5 و6 نقاط توازن مستقرة أو تظهر تقلبات دورية. ومع ذلك، فإن مثل هذه الدورات تختلف عن تلك المنعكسة في معادلتي لوتكا-فولتيرا 1 و2. يمكن أن يكون للدورات المنقولة بواسطة المعادلتين 5 و6 سعة ثابتة ومتوسط كثافات طالما أن الوسط ثابت؛ وبعد حدوث اضطراب، يمكنها العودة إلى اتساعها وكثافتها المتوسطة السابقة. تسمى هذه الدورات التي تتعافى من الاضطرابات بدورات الحد المستقر. يمكن اعتبار التفاعل بين الأرنب والوشق بمثابة دورة حدية مستقرة، ولكنها ليست دورة لوتكا-فولتيرا.[...]
دعونا نفكر في حدوث عدم استقرار الانتشار في نظام المفترس والفريسة، ولكن أولاً سنكتب الشروط التي تضمن حدوث عدم استقرار الانتشار في النظام (1.1) مع n = 2. ومن الواضح أن التوازن (N، N ) محلي (أي[ .. .]
دعنا ننتقل إلى تفسير الحالات المرتبطة بالتعايش طويل الأمد بين المفترس والفريسة. من الواضح أنه في غياب دورات الحد، فإن التوازن المستقر سوف يتوافق مع التقلبات السكانية في بيئة عشوائية، وسوف يتناسب اتساعها مع تشتت الاضطرابات. ستحدث هذه الظاهرة إذا كان لدى المفترس معدل وفيات نسبي مرتفع وفي نفس الوقت درجة عالية من القدرة على التكيف مع فريسة معينة.[...]
دعونا الآن نفكر في كيفية تغير ديناميكيات النظام مع زيادة لياقة المفترس، أي. مع انخفاض b من 1 إلى 0. إذا كانت اللياقة البدنية منخفضة بدرجة كافية، فلن تكون هناك دورات حدودية، ويكون التوازن غير مستقر. ومع زيادة اللياقة البدنية في محيط هذا التوازن قد تظهر دورة مستقرة ومن ثم دورة خارجية غير مستقرة. اعتمادًا على الظروف الأولية (نسبة الكتلة الحيوية المفترسة والفريسة)، يمكن أن يفقد النظام الاستقرار، أي. ترك محيط التوازن، أو سيتم إنشاء تذبذبات مستقرة فيه مع مرور الوقت. مزيد من النمو في اللياقة البدنية يجعل الطبيعة المتذبذبة لسلوك النظام مستحيلة. ومع ذلك، عندما ب [...]
مثال على ردود الفعل السلبية (المثبتة) هو العلاقة بين المفترس والفريسة أو عمل نظام كربونات المحيط (محلول ثاني أكسيد الكربون في الماء: CO2 + H2O -> H2CO3). عادة، تكون كمية ثاني أكسيد الكربون الذائبة في مياه المحيط في حالة توازن جزئي مع تركيز ثاني أكسيد الكربون في الغلاف الجوي. تؤدي الزيادات المحلية في ثاني أكسيد الكربون في الغلاف الجوي بعد الانفجارات البركانية إلى تكثيف عملية التمثيل الضوئي وامتصاصه بواسطة نظام كربونات المحيط. مع انخفاض مستويات ثاني أكسيد الكربون في الغلاف الجوي، يطلق نظام كربونات المحيط ثاني أكسيد الكربون في الغلاف الجوي. ولذلك فإن تركيز ثاني أكسيد الكربون في الغلاف الجوي مستقر تماماً.[...]
[ ...]
كما أشار ر. ريكليفس (1979)، هناك عوامل تساهم في استقرار العلاقات في نظام "المفترس-الفريسة": عدم كفاءة المفترس، ووجود موارد غذائية بديلة للمفترس، وتقليل التأخير في عملية المفترس. رد فعل المفترس، فضلا عن القيود البيئية التي تفرضها البيئة الخارجية على مجموعة أو أخرى من السكان. التفاعلات بين الحيوانات المفترسة والفرائس متنوعة ومعقدة للغاية. وبالتالي، إذا كانت الحيوانات المفترسة فعالة بما فيه الكفاية، فيمكنها تنظيم الكثافة السكانية للفريسة، وإبقائها أقل من القدرة الاستيعابية للبيئة. من خلال تأثيرها على مجموعات الفرائس، تؤثر الحيوانات المفترسة على تطور الخصائص المختلفة للفريسة، مما يؤدي في النهاية إلى التوازن البيئي بين مجموعات الحيوانات المفترسة والفريسة.[...]
إذا توافر أحد الشروط: 0 1/2. إذا كان 6> 1 (كا [...]
يعتمد استقرار الكائنات الحية والبيئة فقط على تفاعل النباتات - الكائنات ذاتية التغذية والكائنات غير المتجانسة العاشبة. الحيوانات المفترسة من أي حجم ليست قادرة على الإخلال بالتوازن البيئي للمجتمع، لأنها في ظل الظروف الطبيعية لا يمكنها زيادة أعدادها بعدد ثابت من الفرائس. لا يجب أن تكون الحيوانات المفترسة متحركة فحسب، بل يمكنها أيضًا أن تتغذى فقط على الحيوانات المتحركة.[...]
لا توجد سمكة أخرى منتشرة على نطاق واسع مثل سمك الكراكي. في عدد قليل من مناطق الصيد في الخزانات القائمة أو المتدفقة، لا يوجد ضغط من أسماك الحراب للحفاظ على التوازن بين الفريسة والمفترس.فقط الخزانات الاصطناعية الحديثة، التي تكون فيها أسماك الحراب أسماكًا غير مرغوب فيها بسبب تكاثر الأسماك الأخرى هناك، لا يتم سكنها بشكل مقصود. هم. يتم تمثيل بايك بشكل جيد للغاية في العالم. يتم القبض عليهم في جميع أنحاء نصف الكرة الشمالي من الولايات المتحدة وكندا إلى أمريكا الشمالية، عبر أوروبا إلى شمال آسيا.[...]
تنشأ هنا إمكانية أخرى للتعايش المستدام، في نطاق ضيق من التكيف العالي نسبيًا. عند الانتقال إلى نظام غير مستقر مع مفترس "جيد" للغاية، قد تنشأ دورة حدود خارجية مستقرة، حيث يتم موازنة تبديد الكتلة الحيوية من خلال تدفقها إلى النظام (الإنتاجية العالية للفريسة). ثم ينشأ موقف غريب عندما تكون على الأرجح قيمتان مميزتان لسعة التذبذبات العشوائية. بعضها يحدث بالقرب من التوازن، والبعض الآخر - بالقرب من دورة الحد، ومن الممكن حدوث تحولات متكررة أكثر أو أقل بين هذه الأنظمة. [...]
المجموعات السكانية الافتراضية التي تتصرف وفقًا للناقلات في الشكل 1. 10.11 أ، موضحة في الشكل. 10.11، -B باستخدام رسم بياني يوضح ديناميكيات نسبة أعداد الحيوانات المفترسة والفرائس وفي الشكل 1. 10.11.5 على شكل رسم بياني لديناميكيات وفرة الحيوانات المفترسة والفريسة مع مرور الوقت. في مجتمع الفرائس، أثناء انتقاله من توازن منخفض الكثافة إلى توازن عالي الكثافة والعودة مرة أخرى، يحدث "تفجر" في الأعداد. وهذا الانفجار في الأعداد ليس نتيجة لتغير واضح بنفس القدر في البيئة. على العكس من ذلك، فإن هذا التغيير في الأرقام يتولد عن التأثير نفسه (مع مستوى صغير من "الضوضاء" في البيئة)، وهو يعكس على وجه الخصوص وجود العديد من حالات التوازن. يمكن استخدام تفكير مماثل لشرح حالات أكثر تعقيدًا للديناميكيات السكانية في المجموعات الطبيعية.[...]
إن أهم خاصية للنظام البيئي هي استقراره وتوازن التبادل والعمليات التي تحدث فيه. تسمى قدرة السكان أو النظم البيئية على الحفاظ على توازن ديناميكي مستقر في الظروف البيئية المتغيرة بالتوازن (homoios - نفس، مماثل، ركود - حالة). ويستند التوازن على مبدأ ردود الفعل. للحفاظ على التوازن في الطبيعة، لا يلزم وجود رقابة خارجية. مثال على التوازن هو النظام الفرعي "المفترس والفريسة"، حيث يتم تنظيم الكثافة السكانية للمفترس والفريسة.[...]
يعمل النظام البيئي الطبيعي (التكاثر الحيوي) بشكل مستقر مع التفاعل المستمر لعناصره، وتداول المواد، ونقل المواد الكيميائية والطاقة والجينية وغيرها من الطاقة والمعلومات من خلال قنوات متسلسلة. وفقًا لمبدأ التوازن، فإن أي نظام طبيعي يمر عبره تدفق من الطاقة والمعلومات يميل إلى تطوير حالة مستقرة. وفي الوقت نفسه، يتم ضمان استقرار النظم البيئية تلقائيًا من خلال آلية التغذية الراجعة. تتكون التغذية الراجعة من استخدام البيانات الواردة من المكونات المُدارة للنظم البيئية لإجراء تعديلات على العملية بواسطة المكونات المُدارة. يمكن وصف العلاقة بين "المفترس" و"الفريسة" التي تمت مناقشتها أعلاه في هذا السياق بمزيد من التفصيل إلى حد ما؛ نعم، في النظام البيئي المائي الأسماك المفترسة(بايك في البركة) تأكل أنواعًا أخرى من الأسماك المفترسة (مبروك الدوع) ؛ إذا زاد عدد مبروك الدوع، فهذا مثال على ردود الفعل الإيجابية؛ يتغذى الكراكي على مبروك الدوع ويقلل أعداده - وهذا مثال على ردود الفعل السلبية ؛ مع زيادة عدد الحيوانات المفترسة، يتناقص عدد الضحايا، كما أن المفترس، الذي يعاني من نقص الغذاء، يقلل أيضًا من نمو سكانه؛ وفي النهاية، في البركة المعنية، تم تحقيق توازن ديناميكي في أعداد كل من سمك الكراكي و مبروك الدوع. يتم الحفاظ على التوازن باستمرار، الأمر الذي من شأنه أن يستبعد اختفاء أي حلقة في السلسلة الغذائية (الشكل 64).[...]
دعنا ننتقل إلى التعميم الأكثر أهمية، وهو أن التفاعلات السلبية تصبح أقل وضوحًا بمرور الوقت إذا كان النظام البيئي مستقرًا بدرجة كافية وبنيته المكانية تسمح بالتكيف المتبادل بين السكان. في الأنظمة النموذجية مثل فريسة مفترسة، الموصوفة في معادلة Lotka-Volterra، إذا لم يتم إدخال مصطلحات إضافية في المعادلة، والتي تميز عمل عوامل التحديد الذاتي للأرقام، فإن التذبذبات تحدث بشكل مستمر ولا تموت (انظر Lewontin، 1969). أظهر بيمنتل (1968؛ انظر أيضًا بيمنتل وستون، 1968) تجريبيًا أن مثل هذه المصطلحات الإضافية قد تعكس تكيفات متبادلة أو جينات وراثية. تعليق. عندما تم إنشاء ثقافات جديدة من أفراد كانوا يتعايشون سابقًا لمدة عامين في ثقافة كانت أعدادهم فيها عرضة لتقلبات كبيرة، اتضح أنهم طوروا التوازن البيئي، حيث يتم "قمع" كل مجموعة من السكان من قبل الآخر إلى هذا الحد. إلى الحد الذي أصبح من الممكن فيه التعايش في توازن أكثر استقرارًا.
نموذج حالة المفترس والفريسة
لنفكر في نموذج رياضي لديناميات التعايش بين نوعين بيولوجيين (مجموعات سكانية) يتفاعلان مع بعضهما البعض وفقًا لنوع "المفترس والفريسة" (الذئاب والأرانب، والحراب، وسمك الشبوط، وما إلى ذلك)، والذي يسمى نموذج فولتر-لوتكا . تم الحصول عليها لأول مرة بواسطة A. Lotka (1925)، وبعد ذلك بقليل وبشكل مستقل عن Lotka، تم تطوير نماذج مماثلة وأكثر تعقيدًا بواسطة عالم الرياضيات الإيطالي V. Volterra (1926)، الذي وضع عمله بالفعل أسس ما يسمى البيئة الرياضية.
يجب أن يكون هناك نوعان بيولوجيان يعيشان معًا في بيئة معزولة. هذا يفترض:
- 1. أن تتمكن الضحية من العثور على ما يكفي من الغذاء للبقاء على قيد الحياة؛
- 2. في كل مرة تلتقي فيها الفريسة بحيوان مفترس، يقوم الأخير بقتل الضحية.
من أجل الدقة، سوف نسميهم الكارب والبايك. يترك
يتم تحديد حالة النظام من خلال الكميات س (ر)و ص (ر)- عدد مبروك الدوع والبايك في المرة الواحدة ز.للحصول على معادلات رياضية تصف تقريبًا ديناميكيات (التغير مع مرور الوقت) للسكان، نتبع ما يلي.
كما هو الحال في نموذج النمو السكاني السابق (انظر القسم 1.1)، لدينا المعادلة بالنسبة للضحايا
أين أ> 0 (معدل المواليد يتجاوز معدل الوفيات)
معامل في الرياضيات او درجة أتعتمد الزيادة في الفريسة على عدد الحيوانات المفترسة (تتناقص مع زيادتها). في أبسط الحالات أ- أ - فجي (أ>0، ص>0).ثم بالنسبة لحجم الفريسة، لدينا المعادلة التفاضلية
بالنسبة لمجموعة من الحيوانات المفترسة، لدينا المعادلة

أين ب> 0 (الوفيات تتجاوز معدل المواليد).
معامل في الرياضيات او درجة بيتم تقليل انخفاض الحيوانات المفترسة إذا كانت هناك فريسة لتتغذى عليها. في أبسط الحالات يمكننا أن نأخذ ب - ذ -سكس (ذ > 0, س> 0). ثم بالنسبة لحجم التجمعات المفترسة نحصل على المعادلة التفاضلية

وبالتالي فإن المعادلتين (1.5) و (1.6) تمثلان نموذجاً رياضياً لمشكلة التفاعل السكاني قيد النظر. في هذا النموذج المتغيرات س، صهي حالة النظام، والمعاملات تميز بنيته. النظام غير الخطي (1.5)، (1.6) هو نموذج فولتير-لوتكا.
يجب استكمال المعادلتين (1.5) و (1.6) بالشروط الأولية - مع إعطاء قيم المجموعات السكانية الأولية.
دعونا الآن نحلل النموذج الرياضي المبني.
دعونا نبني صورة الطور للنظام (1.5)، (1.6) (بمعنى المشكلة X> 0، الخامس >0). بقسمة المعادلة (1.5) على المعادلة (1.6)، نحصل على معادلة ذات متغيرات قابلة للفصل
باستخدام هذه المعادلة، لدينا
العلاقة (1.7) تعطي معادلة مسارات الطور بشكل ضمني. النظام (1.5)، (1.6) لديه حالة ثابتة تحدد من

من المعادلات (1.8) نحصل على (بما أن l* F 0، ص* F 0)
تحدد المساواة (1.9) موضع التوازن (نقطة عن)(الشكل 1.6).

يمكن تحديد اتجاه الحركة على طول مسار المرحلة من خلال هذه الاعتبارات. يجب أن يكون هناك عدد قليل من الصليبيين. ز. x ~ 0، ثم من المعادلة (1.6) y
جميع مسارات المرحلة (باستثناء النقطة 0) منحنيات مغلقة تغطي موضع التوازن. حالة التوازن تتوافق مع عدد ثابت من x" و y" من مبروك الدوع والبايك. يتكاثر مبروك الدوع ويأكله الكراكي ويموت ولكن عدده وعدد الآخرين لا يتغير. "تتوافق مسارات الطور المغلق مع تغير دوري في عدد مبروك الدوع والبايك. علاوة على ذلك، فإن المسار الذي تتحرك عبره نقطة الطور يعتمد على الظروف الأولية. دعونا نفكر في كيفية تغير الحالة على طول مسار الطور. دع النقطة تكون في الموقف أ(الشكل 1.6). يوجد عدد قليل من مبروك الدوع هنا والعديد من سمك الكراكي. ليس لدى الحراب ما تأكله، وتموت تدريجيًا وتقريبًا
تختفي تماما. لكن عدد مبروك الدوع يتناقص أيضًا إلى الصفر تقريبًا
في وقت لاحق فقط، عندما كان هناك عدد أقل من الحراب فييبدأ عدد مبروك الدوع في الزيادة؛ يزداد معدل نموهم ويزداد عددهم - ويحدث هذا حتى هذه النقطة تقريبًا في.لكن الزيادة في عدد مبروك الدوع تؤدي إلى تباطؤ عملية انقراض الشوك ويبدأ عددها في النمو (يوجد المزيد من الطعام) - مؤامرة شمس.بعد ذلك هناك الكثير من الحراب، يأكلون مبروك الدوع ويأكلونهم جميعًا تقريبًا (القسم 1). القرص المضغوط).بعد ذلك، يبدأ الرمح في الموت مرة أخرى وتتكرر العملية لمدة 5-7 سنوات تقريبًا. في التين. 1.7 منحنيات مبنية نوعيًا للتغيرات في عدد مبروك الدوع والبايك اعتمادًا على الوقت. تتناوب الحدود القصوى للمنحنيات، ويتخلف الحد الأقصى لعدد الحراب عن الحد الأقصى لمبروك الدوع.

هذا السلوك نموذجي لمختلف أنظمة المفترس والفريسة. دعونا الآن نفسر النتائج التي تم الحصول عليها.
على الرغم من أن النموذج الذي تم النظر فيه هو الأبسط وفي الواقع كل شيء يحدث أكثر تعقيدًا، إلا أنه جعل من الممكن شرح بعض الأشياء الغامضة الموجودة في الطبيعة. إن قصص الصيادين عن الفترات التي "يقفز فيها الرمح في أيديهم" مفهومة، وقد تم شرح تواتر الأمراض المزمنة وما إلى ذلك.
دعونا نلاحظ واحدا آخر استنتاج مثير للاهتمام، والتي يمكن صنعها من الشكل. 1.6. إذا في هذه النقطة رهناك اصطياد سريع للحراب (في مصطلحات أخرى - إطلاق النار على الذئاب)، ثم "يقفز" النظام إلى النقطة س،ويحدث المزيد من الحركة على طول مسار مغلق بحجم أصغر، وهو أمر متوقع بشكل بديهي. إذا قمنا بتقليل عدد الحراب عند نقطة ما ص،ثم سوف يذهب النظام إلى هذه النقطة س،وسيحدث المزيد من الحركة على طول المسار حجم أكبر. ستزداد سعة التذبذبات. وهذا أمر غير بديهي، لكنه يفسر هذه الظاهرة على وجه التحديد: نتيجة لإطلاق النار على الذئاب، تزداد أعدادها بمرور الوقت. وبالتالي فإن اختيار لحظة التصوير مهم في هذه الحالة.
لنفترض أن مجموعتين من الحشرات (على سبيل المثال، حشرة المن والخنفساء التي تأكل حشرات المن) كانتا في حالة توازن طبيعي س-س*،ص = ص*(نقطة عنفي التين. 1.6). فكر في تأثير استخدام مبيد حشري مرة واحدة في القتل س> 0 من الضحايا و ذ> 0 من الحيوانات المفترسة دون تدميرها بالكامل. يؤدي انخفاض عدد كلا المجموعتين إلى حقيقة أن النقطة الممثلة من الموضع عنسوف "يقفز" أقرب إلى أصل الإحداثيات، حيث س> 0, ذ 0 (الشكل 1.6) ويترتب على ذلك أنه نتيجة لعمل مبيد حشري مصمم لتدمير الضحايا (المن)، يزداد عدد الضحايا (المن)، وعدد الحيوانات المفترسة ( الخنافس) يتناقص. وتبين أن عدد الحيوانات المفترسة قد يصبح صغيراً لدرجة أنها ستواجه خطر الانقراض الكامل لأسباب أخرى (الجفاف، المرض، إلخ). وبالتالي، فإن استخدام المبيدات الحشرية (ما لم تدمر الحشرات الضارة بالكامل تقريبًا) يؤدي في النهاية إلى زيادة أعداد تلك الحشرات التي تم التحكم في أعدادها من قبل الحشرات المفترسة الأخرى. تم وصف مثل هذه الحالات في كتب علم الأحياء.
وبشكل عام فإن معدل نمو عدد الضحايا أيعتمد على كل من "L" و y: أ= a(x, y) (بسبب وجود الحيوانات المفترسة وبسبب القيود الغذائية).
مع تغيير بسيط في النموذج (1.5)، (1.6)، يتم إضافة حدود صغيرة إلى الطرف الأيمن من المعادلات (مع الأخذ في الاعتبار، على سبيل المثال، تنافس مبروك الدوع على الغذاء والبايك على مبروك الدوع)
هنا 0 في «1.
وفي هذه الحالة فإن الاستنتاج حول دورية العملية (عودة النظام إلى حالته الأصلية)، والذي ينطبق على النموذج (1.5)، (1.6)، يفقد صحته. حسب نوع التعديلات الصغيرة/ و زالمواقف الموضحة في الشكل ممكنة. 1.8.

في الحالة (1) حالة التوازن عنمستمر. ولأي شروط أولية أخرى بعد الكفاية لحظة عظيمةهذا هو ما تم تثبيته.
وفي الحالة (2)، فإن النظام "يصبح في حالة من الفوضى". الحالة الثابتة غير مستقرة. يقع مثل هذا النظام في النهاية ضمن هذا النطاق من القيم Xو أن النموذج لم يعد قابلاً للتطبيق.
في الحالة (3) في نظام ذو حالة ثابتة غير مستقرة عنيتم إنشاء نظام دوري مع مرور الوقت. على عكس النموذج الأصلي (1.5)، (1.6)، في هذا النموذج لا يعتمد النظام الدوري للحالة المستقرة على الظروف الأولية. في البداية انحراف صغير عن الحالة المستقرة عنلا يؤدي إلى تقلبات صغيرة حولها عن، كما هو الحال في نموذج فولتيرا-لوتكا، ولكن لتذبذبات ذات سعة محددة جيدًا (ومستقلة عن صغر الانحراف).
في و. يصف أرنولد نموذج فولتيرا-لوتكا بأنه جامد لأنه يمكن أن يؤدي تغييرها البسيط إلى استنتاجات مختلفة عن تلك المذكورة أعلاه. للحكم على أي من الحالات الموضحة في الشكل؟ 1.8، المطبق في هذا النظام، ضروري للغاية معلومات إضافيةحول النظام (حول نوع التعديلات الصغيرة/ و ز).
هنا، على النقيض من (3.2.1)، فإن علامات (-012) و (+a2i) مختلفة. وكما في حالة المنافسة (نظام المعادلات (2.2.1)) فإن أصل الإحداثيات (1) لهذا النظام هو نقطة خاصة من نوع "العقدة غير المستقرة". ثلاث حالات مستقرة أخرى محتملة:

المعنى البيولوجي يتطلب كميات إيجابية س ص س 2. بالنسبة للتعبير (3.3.4) فهذا يعني ذلك
إذا كان معامل المنافسة بين الحيوانات المفترسة أ,22 = 0، الشرط (3.3.5) يؤدي إلى الشرط ai2
يتم عرض الأنواع المحتملة لصور الطور لنظام المعادلات (3.3.1) في الشكل. 3.2 أ-ج. Isoclins من الظلال الأفقية هي خطوط مستقيمة
وتكون الخطوط المتساوية للظلال الرأسية مستقيمة
من الشكل. 3.2 يظهر ما يلي. قد يكون لنظام المفترس والفريسة (3.3.1) وضع توازن مستقر تنقرض فيه مجموعة الفرائس تمامًا (س = 0) وبقيت الحيوانات المفترسة فقط (النقطة 2 في الشكل 3.26). ومن الواضح أن مثل هذا الوضع لا يمكن أن يتحقق إلا إذا، بالإضافة إلى نوع الضحايا المعنيين، Xالمفترس X2 لديها مصادر طاقة إضافية. تنعكس هذه الحقيقة في النموذج من خلال حد إيجابي على الجانب الأيمن من المعادلة لـ xs. النقطتان المفردتان (1) و (3) (الشكل 3.26) غير مستقرة. الاحتمال الثاني هو حالة ثابتة مستقرة، حيث ينقرض سكان الحيوانات المفترسة تمامًا وتبقى الفريسة فقط - النقطة المستقرة (3) (الشكل 3.2 أ). هنا النقطة المفردة (1) هي أيضًا عقدة غير مستقرة.
أخيرًا، الاحتمال الثالث هو التعايش المستقر بين مجموعات الحيوانات المفترسة والفريسة (الشكل 3.2 ج)، والتي يتم التعبير عن أعدادها الثابتة بالصيغ (3.3.4). دعونا نفكر في هذه الحالة بمزيد من التفصيل.
لنفترض أن معاملات المنافسة بين الأنواع تساوي الصفر (منظمة العفو الدولية= 0، ط = 1، 2). لنفترض أيضًا أن الحيوانات المفترسة تتغذى فقط على فريسة هذا النوع Xوفي غيابهم يموتون بمعدل C2 (في (3.3.5) C2).
دعونا نجري دراسة مفصلة لهذا النموذج، باستخدام التدوين الأكثر قبولا على نطاق واسع في الأدبيات. تجديد

أرز. 3.2. موقع الخطوط المتساوية الرئيسية على صورة الطور لنظام فولتيرا المفترس والفريسة لنسب مختلفة من المعلمات: أ- عن -
معأنا ج2ج2
1، 3 - غير مستقر، 2 - نقطة مفردة مستقرة؛ الخامس -
1، 2، 3 - غير مستقر، 4 - نقطة مفردة مستقرة كبيرة
نظام المفترس والفريسة في هذه الرموز له الشكل:

سوف نقوم بدراسة خواص حلول النظام (3.3.6) على مستوى الطور ن1
على2
يحتوي النظام على حلين ثابتين. ويمكن تحديدها بسهولة عن طريق مساواة الجوانب اليمنى من النظام بالصفر. نحن نحصل: 
ومن هنا الحلول الثابتة:

دعونا نلقي نظرة فاحصة على الحل الثاني. دعونا نجد التكامل الأول للنظام (3.3.6) الذي لا يحتوي على ر.دعونا نضرب المعادلة الأولى في -72، والثانية في -71 ونجمع النتائج. نحن نحصل:
الآن دعونا نقسم المعادلة الأولى على نوتتضاعف بها € 2، واقسم الثاني على JV 2 واضرب في ه.دعنا نضيف النتائج مرة أخرى:
بمقارنة (3.3.7) و (3.3.8) نجد أن:

بالتكامل نحصل على:

هذا هو التكامل الأول المطلوب. وبالتالي، فإن النظام (3.3.6) محافظ لأنه يحتوي على تكامل أولي للحركة، وهي الكمية التي تكون دالة لمتغيرات النظام نو ن2 ومستقلة عن الزمن. تتيح لنا هذه الخاصية أن نبني لأنظمة فولتيرا نظامًا من المفاهيم المشابهة للميكانيكا الإحصائية (انظر الفصل 5)، حيث تلعب قيمة الطاقة للنظام، والتي تكون ثابتة بمرور الوقت، دورًا مهمًا.
لكل ثابت من > 0 (الذي يتوافق مع بعض البيانات الأولية)، يتوافق التكامل مع مسار معين على المستوى ن1 على2 ، بمثابة مسار النظام (3.3.6).
دعونا نفكر طريقة الرسمبناء المسار الذي اقترحه فولتيرا نفسه. لاحظ أن الجزء الأيمنالصيغة (3.3.9) تعتمد فقط على D g 2، والصيغة اليسرى تعتمد فقط على ن.دعونا نشير
ومن (3.3.9) يتبع ذلك بين Xو يهناك علاقة تناسبية
في التين. 3.3 يُظهر الأرباع الأولى لأنظمة الإحداثيات الأربعة شوي، نوي, ن2 ثورو د جي 1 0 ن2 بحيث يكون لهم جميعا أصل مشترك.
في الزاوية اليسرى العليا (الربع نوى)تم رسم رسم بياني للدالة (3.3.8) في الجزء السفلي الأيمن (الربع ن2 ثور)- الرسم البياني الوظيفي ي.الوظيفة الأولى لها دقيقة في ني =والثاني - بحد أقصى ن2 = ?-
وأخيرا، في الربع XOYدعونا نبني خطًا مستقيمًا (3.3.12) لبعض الأشياء الثابتة مع.
دعونا نضع علامة على هذه النقطة نعلى المحور على. هذه النقطة يتوافق مع قيمة معينة ص(ن 1) من السهل العثور عليه عن طريق رسم عمودي

أرز. 3.3.
خلال نحتى يتقاطع مع المنحنى (3.3.10) (انظر الشكل 3.3). في المقابل، تتوافق القيمة K(D^) مع نقطة معينة M على الخط ي = cXوبالتالي بعض القيمة ×(ن) = ص (ن) / ج،والتي يمكن العثور عليها عن طريق رسم الخطوط المتعامدة أكون.و (دكتور في الطب)القيمة التي تم العثور عليها (تم تحديد هذه النقطة في الشكل بالحرف د)نقطتين تتوافق رو زعلى المنحنى (3.3.11). وباستخدام هذه النقاط، ورسم الخطوط المتعامدة، سنجد نقطتين في وقت واحد ه"و ه"، ملقاة على المنحنى (3.3.9). إحداثياتها:

رسم عمودي أكون.، تجاوزنا المنحنى (3.3.10) عند نقطة أخرى في.هذه النقطة يتوافق مع نفسه رو سعلى المنحنى (3.3.11) ونفس الشيء نو SCH.تنسيق نيمكن العثور على هذه النقطة بإسقاط العمودي من فيلكل محور على.حتى نحصل على النقاط F"و F"، يقع أيضًا على المنحنى (3.3.9).
قادمة من نقطة مختلفة ن،وبنفس الطريقة نحصل على أربع نقاط جديدة تقع على المنحنى (3.3.9). الاستثناء سيكون النقطة ني= ?2/72- وعلى هذا نحصل على نقطتين فقط: لو ل.ستكون هذه هي النقاط السفلية والعليا للمنحنى (3.3.9).
لا يمكن أن تبدأ من القيم ن، ومن القيم ن2 . التوجه من ن2 إلى المنحنى (3.3.11)، ثم نصعد إلى الخط المستقيم Y = cX، ومن هناك نعبر المنحنى (3.3.10)، نجد أيضًا أربع نقاط من المنحنى (3.3.9). الاستثناء سيكون النقطة لا= 1/71- وعلى هذا نحصل على نقطتين فقط: زو ل.ستكون هذه هي أقصى النقاط في أقصى اليسار وفي أقصى اليمين في المنحنى (3.3.9). بسؤال مختلف نو ن2 وبعد أن حصلنا على الكثير من النقاط، وربطها، سنقوم تقريبًا ببناء المنحنى (3.3.9).
يتضح من البناء أن هذا منحنى مغلق يحتوي في داخله على النقطة 12 = (؟2/721؟1/71)” بدءًا من بيانات أولية معينة نيو وN20. أخذ قيمة أخرى لـ C، أي من البيانات الأولية الأخرى، نحصل على منحنى مغلق آخر لا يتقاطع مع الأول ويحتوي أيضًا على النقطة (؟2/721؟1/71)1 داخل نفسه. وبالتالي، فإن عائلة المسارات (3.3.9) هي عائلة من الخطوط المغلقة المحيطة بالنقطة 12 (انظر الشكل 3.3). دعونا ندرس نوع استقرار هذه النقطة المفردة باستخدام طريقة ليابونوف.
منذ جميع المعلمات ه 1، 2، 71،72 إيجابية، نقطة (يقع N[ في الربع الموجب لمستوى الطور. ويعطي الخط الخطي للنظام بالقرب من هذه النقطة ما يلي:

هنا ن (ر)و7i2(N1، ن2 :
المعادلة المميزة للنظام (3.3.13):

جذور هذه المعادلة خيالية بحتة:

وهكذا، تظهر دراسة النظام أن المسارات القريبة من النقطة المفردة يتم تمثيلها بواسطة قطع ناقص متحدة المركز، والنقطة المفردة نفسها هي المركز (الشكل 3.4). يحتوي نموذج فولتيرا قيد النظر أيضًا على مسارات مغلقة بعيدة عن نقطة المفرد، على الرغم من أن شكل هذه المسارات يختلف بالفعل عن المسارات الإهليلجية. سلوك المتغيرات ني، ن2 مع مرور الوقت هو مبين في الشكل. 3.5.

أرز. 3.4.

أرز. 3.5. الاعتماد على أعداد الفرائس نأنا والمفترس ن2 من وقت
النقطة المفردة من النوع المركزي تكون مستقرة، ولكن ليست مقاربة. دعونا نبين مع هذا المثال ما هو هذا. دع التردد أحمق)وتحدث LGgM بطريقة تتحرك فيها النقطة الممثلة على طول مستوى الطور على طول المسار 1 (انظر الشكل 3.4). في اللحظة التي تكون فيها النقطة في الموضع M، تتم إضافة عدد معين من الأفراد إلى النظام من الخارج ن 2، بحيث تقفز النقطة الممثلة من النقطة مللنقطة A/". وبعد ذلك، إذا ترك النظام لنفسه مرة أخرى، فستحدث التذبذبات نيو ن2 ستحدث بالفعل بسعات أكبر من ذي قبل، وتتحرك النقطة الممثلة على طول المسار 2. وهذا يعني أن التذبذبات في النظام غير مستقرة: فهي تغير خصائصها إلى الأبد عندما تأثير خارجي. في المستقبل، سننظر في النماذج التي تصف الأنظمة التذبذبية المستقرة ونوضح أنه على مستوى الطور، يتم تصوير مثل هذه الحركات الدورية المستقرة المقاربة باستخدام دورات الحد.
في التين. يوضح الشكل 3.6 المنحنيات التجريبية - التقلبات في عدد الحيوانات ذات الفراء في كندا (وفقًا لشركة خليج هدسون). يتم إنشاء هذه المنحنيات بناءً على بيانات حول عدد الجلود المحصودة. فترات التقلبات في أعداد الأرانب البرية (الفريسة) والوشق (الحيوانات المفترسة) هي نفسها تقريبًا وتتراوح من 9 إلى 10 سنوات. في هذه الحالة، يكون الحد الأقصى لعدد الأرانب البرية، كقاعدة عامة، متقدمًا على الحد الأقصى لعدد الوشق بسنة واحدة.
شكل هذه المنحنيات التجريبية أقل انتظامًا بكثير من المنحنيات النظرية. ومع ذلك، في هذه الحالة، يكفي أن يضمن النموذج تطابق أهم خصائص المنحنيات النظرية والتجريبية، أي. قيم السعة وتحولات الطور بين التقلبات في أعداد الحيوانات المفترسة والفرائس. العيب الأكثر خطورة في نموذج فولتيرا هو عدم استقرار الحلول لنظام المعادلات. في الواقع، كما ذكر أعلاه، فإن أي تغيير عشوائي في وفرة نوع أو آخر يجب أن يؤدي، وفقًا للنموذج، إلى تغيير في سعة التذبذبات لكلا النوعين. بطبيعة الحال، في الظروف الطبيعيةتتعرض الحيوانات لعدد لا يحصى من هذه التأثيرات العشوائية. وكما يتبين من المنحنيات التجريبية، فإن مدى التقلبات في أعداد الأنواع يختلف قليلاً من سنة إلى أخرى.
يعتبر نموذج فولتيرا مرجعا (أساسيا) لعلم البيئة الرياضي بنفس القدر الذي يعتبر فيه نموذج المذبذب التوافقي أساسيا في العلوم الكلاسيكية و ميكانيكا الكم. وباستخدام هذا النموذج المبني على أفكار مبسطة للغاية حول طبيعة الأنماط التي تصف سلوك النظام، رياضي بحت
الفصل 3

أرز. 3.6. المنحنيات الحركية لعدد الحيوانات ذات الفراء وفقًا لبيانات شركة Hudson Bay Fur Company (Seton-Thomson، 1987) تم من خلال استنتاج حول الطبيعة النوعية لسلوك مثل هذا النظام - حول وجود التقلبات السكانية في مثل هذا النظام. وبدون بناء نموذج رياضي واستخدامه، سيكون مثل هذا الاستنتاج مستحيلا.
في ما ناقشناه أعلاه في شكل بسيطيعاني نظام فولتيرا من عيبين أساسيين ومترابطين. تم تخصيص أدبيات بيئية ورياضية واسعة النطاق لـ "القضاء عليها". أولاً، يؤدي إدراج أي عوامل إضافية، مهما كانت صغيرة، في النموذج إلى تغيير سلوك النظام نوعيًا. العيب "البيولوجي" الثاني للنموذج هو أنه لا يتضمن الخصائص الأساسية المتأصلة في أي زوج من المجموعات السكانية التي تتفاعل وفقًا لمبدأ المفترس والفريسة: تأثير تشبع المفترس، والموارد المحدودة للمفترس والفريسة حتى مع وجود فائض من الفرائس، وإمكانية وجود حد أدنى لعدد الفرائس المتاحة للمفترس، وما إلى ذلك.
من أجل القضاء على هذه العيوب، تم اقتراح تعديلات مختلفة على نظام فولتيرا من قبل مؤلفين مختلفين. سيتم مناقشة أكثرها إثارة للاهتمام في القسم 3.5. سنركز هنا فقط على النموذج الذي يأخذ في الاعتبار القيود الذاتية في نمو كلا المجموعتين. يوضح مثال هذا النموذج بوضوح كيف يمكن أن تتغير طبيعة القرارات عندما تتغير معلمات النظام.
لذلك، نحن نعتبر النظام

يختلف النظام (3.3.15) عن النظام المذكور سابقا (3.3.6) بوجود حدود من الصيغة -7 على الجانب الأيمن من المعادلات الأمم المتحدة,
تعكس هذه المصطلحات حقيقة أن أعداد الفرائس لا يمكن أن تنمو إلى أجل غير مسمى حتى في غياب الحيوانات المفترسة بسبب محدودية الموارد الغذائية والموائل المحدودة. يتم فرض نفس "القيود الذاتية" على سكان الحيوانات المفترسة.
للعثور على أعداد ثابتة من الأنواع iVi و ن2 دعونا نساوي الأطراف اليمنى من معادلات النظام (3.3.15) بالصفر. إن الحلول ذات الأعداد الصفرية من الحيوانات المفترسة أو الفرائس لن تهمنا الآن. لذلك، النظر في نظام جبري
المعادلات  قرارها
قرارها
يعطينا إحداثيات النقطة المفردة. هنا ينبغي فرض شرط إيجابية الأرقام الثابتة على معلمات النظام: ن> 0 و ن2 > 0. جذور المعادلة المميزة للنظام الخطي في جوار النقطة المفردة (3.3.16):

ومن التعبير عن الأعداد المميزة يتضح أنه إذا تحقق الشرط
ثم تخضع أعداد الحيوانات المفترسة والفرائس لتذبذبات ضعيفة بمرور الوقت، ويكون للنظام نقطة مفردة غير صفرية وتركيزًا ثابتًا. تظهر صورة الطور لمثل هذا النظام في الشكل. 3.7 أ.
لنفترض أن المعلمات في عدم المساواة (3.3.17) تغير قيمها بحيث يصبح الشرط (3.3.17) مساواة. عندها تكون الأعداد المميزة للنظام (3.3.15) متساوية، وستكون نقطة المفرد الخاصة به على الحدود بين مناطق البؤر والعقد المستقرة. عندما يتم عكس إشارة المتباينة (3.3.17)، تصبح النقطة المفردة عقدة مستقرة. تظهر صورة الطور للنظام في هذه الحالة في الشكل. 3.76.
وكما في حالة المجتمع الواحد يمكن تطوير نموذج عشوائي للنموذج (3.3.6) ولكن لا يمكن الحصول على حل صريح له. ولذلك، فإننا سوف تقتصر على الاعتبارات العامة. لنفترض، على سبيل المثال، أن نقطة التوازن تقع على مسافة معينة من كل محور. ثم بالنسبة لمسارات الطور التي تكون عليها قيم JVj، ن2 تظل كبيرة بما فيه الكفاية، فإن النموذج الحتمي سيكون مرضيا تماما. ولكن إذا كان في مرحلة ما


أرز. 3.7. صورة المرحلة للنظام (3.3.15): أ -عندما يتم استيفاء العلاقة (3.3.17) بين المعلمات؛ ب- عند إجراء علاقة عكسية بين المعلمات
مسار المرحلة، أي متغير ليس كبيرا جدا، ثم يمكن أن تصبح التقلبات العشوائية كبيرة. وهي تؤدي إلى أن النقطة الممثلة تتحرك إلى أحد المحاور، مما يعني انقراض الأنواع المقابلة لها. وهكذا، يتبين أن النموذج العشوائي غير مستقر، لأن "الانجراف" العشوائي يؤدي عاجلاً أم آجلاً إلى انقراض أحد الأنواع. في هذا النوع من النماذج، ينقرض الحيوان المفترس في النهاية، إما عن طريق الصدفة أو بسبب القضاء على فرائسه أولاً. يشرح النموذج العشوائي لنظام المفترس والفريسة جيدًا تجارب Gause (Gause, 1934; 2000)، حيث تقوم الشركات الهدبية باراميتوم كانداتومكان بمثابة ضحية لأهداب آخر ديدينيوم ناساتوم- المفترس. كانت أرقام التوازن المتوقعة حسب المعادلات الحتمية (3.3.6) في هذه التجارب حوالي خمسة أفراد فقط من كل نوع، لذلك ليس من المستغرب أنه في كل تجربة متكررة تموت الحيوانات المفترسة أو الفريسة بسرعة كبيرة (ومن ثم الحيوانات المفترسة) .
لذلك، فإن تحليل نماذج فولتيرا للتفاعل بين الأنواع يظهر أنه على الرغم من التنوع الكبير في أنواع سلوك مثل هذه الأنظمة، إلا أنه لا يمكن أن تكون هناك تقلبات غير مقيدة في الأعداد في نموذج الأنواع المتنافسة على الإطلاق. في نموذج المفترس والفريسة، تظهر التذبذبات غير المخمدة نتيجة الاختيار شكل خاصالمعادلات النموذجية (3.3.6). في هذه الحالة، يصبح النموذج غير تقريبي، مما يدل على عدم وجود آليات في مثل هذا النظام تسعى إلى الحفاظ على حالته. ومع ذلك، لوحظت مثل هذه التذبذبات في الطبيعة والتجربة. كانت الحاجة إلى تفسيرهم النظري بمثابة أحد أسباب صياغة أوصاف النماذج بشكل أكبر منظر عام. ويخصص القسم 3.5 للنظر في مثل هذه النماذج المعممة.