Решаване на уравнения и неравенства с модулчесто създава затруднения. Въпреки това, ако разбирате добре какво е абсолютната стойност на число, И как правилно да разширяваме изрази, съдържащи знак за модул, тогава присъствието в уравнението израз под знака за модул, престава да бъде пречка за решаването му.

Малко теория. Всяко число има две характеристики: абсолютната стойност на числото и неговия знак.

Например числото +5 или просто 5 има знак „+“ и абсолютна стойност 5.

Числото -5 има знак "-" и абсолютна стойност 5.

Абсолютните стойности на числата 5 и -5 са 5.

Абсолютната стойност на число x се нарича модул на числото и се означава с |x|.

Както виждаме, модулът на числото е равен на самото число, ако това число е по-голямо или равно на нула, и на това число с обратен знак, ако това число е отрицателно.

Същото се отнася за всички изрази, които се появяват под знака за модул.

Правилото за разширяване на модула изглежда така:

|f(x)|= f(x), ако f(x) ≥ 0, и

|f(x)|= - f(x), ако f(x)< 0

Например |x-3|=x-3, ако x-3≥0 и |x-3|=-(x-3)=3-x, ако x-3<0.

За да решите уравнение, съдържащо израз под знака за модул, първо трябва разширяване на модул според правилото за разширяване на модула.

Тогава нашето уравнение или неравенство става в две различни уравнения, съществуващи на два различни числови интервала.

Едно уравнение съществува в числов интервал, на който изразът под знака за модул е ​​неотрицателен.

И второто уравнение съществува в интервала, в който изразът под знака за модул е ​​отрицателен.

Нека да разгледаме един прост пример.

Нека решим уравнението:

|x-3|=-x 2 +4x-3

1. Да отворим модула.

|x-3|=x-3, ако x-3≥0, т.е. ако x≥3

|x-3|=-(x-3)=3-x, ако x-3<0, т.е. если х<3

2. Получихме два числови интервала: x≥3 и x<3.

Нека разгледаме в какви уравнения се трансформира оригиналното уравнение на всеки интервал:

A) За x≥3 |x-3|=x-3 и нашето нараняване има формата:

внимание! Това уравнение съществува само в интервала x≥3!

Нека отворим скобите и представим подобни термини:

и реши това уравнение.

Това уравнение има корени:

x 1 =0, x 2 =3

внимание! тъй като уравнението x-3=-x 2 +4x-3 съществува само в интервала x≥3, ние се интересуваме само от онези корени, които принадлежат на този интервал. Това условие се изпълнява само от x 2 =3.

Б) При х<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

внимание! Това уравнение съществува само в интервала x<3!

Нека отворим скобите и представим подобни термини. Получаваме уравнението:

x 1 =2, x 2 =3

внимание! тъй като уравнението 3-x=-x 2 +4x-3 съществува само в интервала x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

И така: от първия интервал вземаме само корена x=3, от втория - корена x=2.

Модулът е абсолютната стойност на израза. За да посочите по някакъв начин модул, обичайно е да използвате прави скоби. Стойността, оградена в четни скоби, е стойността, която се взема по модул. Процесът на решаване на всеки модул се състои в отваряне на онези много прави скоби, които на математически език се наричат ​​модулни скоби. Тяхното разкриване става съгласно определен брой правила. Също така, в реда на решаване на модулите, се намират наборите от стойности на тези изрази, които са били в модулните скоби. В повечето случаи модулът се разширява по такъв начин, че изразът, който е бил подмодулен, получава както положителни, така и отрицателни стойности, включително стойността нула. Ако изхождаме от установените свойства на модула, тогава в процеса се компилират различни уравнения или неравенства от оригиналния израз, които след това трябва да бъдат решени. Нека да разберем как да решаваме модули.

Процес на решение

Решаването на модул започва с написването на оригиналното уравнение с модула. За да отговорите на въпроса как да решавате уравнения с модул, трябва да го отворите напълно. За да се реши такова уравнение, модулът се разширява. Трябва да се вземат предвид всички модулни изрази. Необходимо е да се определи при какви стойности на неизвестните количества, включени в неговия състав, модулният израз в скоби става нула. За да направите това, достатъчно е да приравните израза в модулни скоби към нула и след това да изчислите решението на полученото уравнение. Намерените стойности трябва да бъдат записани. По същия начин вие също трябва да определите стойността на всички неизвестни променливи за всички модули в това уравнение. След това трябва да започнете да дефинирате и разглеждате всички случаи на съществуване на променливи в изрази, когато те са различни от стойността нула. За да направите това, трябва да запишете някаква система от неравенства, съответстваща на всички модули в първоначалното неравенство. Неравенствата трябва да бъдат написани така, че да покриват всички налични и възможни стойности за променлива, които се намират на числовата ос. След това трябва да начертаете същата тази числова линия за визуализация, върху която по-късно да нанесете всички получени стойности.

Вече почти всичко може да се направи в интернет. Модулът не прави изключение от правилото. Можете да го решите онлайн на един от многото съвременни ресурси. Всички онези стойности на променливата, които са в нулевия модул, ще бъдат специално ограничение, което ще се използва в процеса на решаване на модулното уравнение. В оригиналното уравнение трябва да отворите всички налични модулни скоби, като същевременно промените знака на израза, така че стойностите на желаната променлива да съвпадат с тези стойности, които се виждат на числовата линия. Полученото уравнение трябва да бъде решено. Стойността на променливата, която ще бъде получена по време на решаването на уравнението, трябва да бъде проверена спрямо ограничението, което е зададено от самия модул. Ако стойността на променливата напълно удовлетворява условието, тогава тя е правилна. Всички корени, които ще бъдат получени по време на решаването на уравнението, но няма да отговарят на ограниченията, трябва да бъдат изхвърлени.

МБОУ СОУ No17 гр. Иваново

« Уравнения с модул"
Методическа разработка

Компилиран

учител по математика

Лебедева Н.В.

20010 г

Обяснителна бележка

Глава 1 Въведение

Раздел 2. Основни свойства Раздел 3. Геометрична интерпретация на понятието модул на число Раздел 4. Графика на функцията y = |x| Раздел 5. Конвенции

Глава 2. Решаване на уравнения, съдържащи модул

Раздел 1. Уравнения от вида |F(x)| = m (най-простият) Раздел 2. Уравнения от вида F(|x|) = m Раздел 3. Уравнения от вида |F(x)| = G(x) Раздел 4. Уравнения от вида |F(x)| = ± F(x) (най-красивата) Раздел 5. Уравнения от вида |F(x)| = |G(x)| Раздел 6. Примери за решаване на нестандартни уравнения Раздел 7. Уравнения от вида |F(x)| + |G(x)| = 0 Раздел 8. Уравнения от вида |a 1 x ± b 1 | ± |a 2 x ± в 2 | ± …|a n x ± в n | = m Раздел 9. Уравнения, съдържащи няколко модула

Глава 3. Примери за решаване на различни уравнения с модул.

Раздел 1. Тригонометрични уравнения Раздел 2. Експоненциални уравнения Раздел 3. Логаритмични уравнения Раздел 4. Ирационални уравнения Раздел 5. Разширени задачи Отговори на упражнения Библиография

Обяснителна бележка.

Концепцията за абсолютна стойност (модул) на реално число е една от основните му характеристики. Тази концепция е широко разпространена в различни раздели на физическите, математическите и техническите науки. В практиката на преподаване на курсове по математика в средните училища в съответствие с Програмата на Министерството на отбраната на Руската федерация понятието „абсолютна стойност на число“ се среща многократно: в 6-ти клас дефиницията на модул и въвежда се геометричното му значение; в 8. клас се формира понятието абсолютна грешка, разглежда се решаването на най-простите уравнения и неравенства, съдържащи модул, и се изучават свойствата на аритметичния корен квадратен; в 11 клас понятието се намира в раздела „Корен н-та степен“.Преподавателският опит показва, че учениците често срещат трудности при решаването на задачи, изискващи познаване на този материал, и често ги пропускат, без да започнат да ги изпълняват. Текстовете на изпитните задачи за курсовете за 9. и 11. клас също включват подобни задачи. Освен това изискванията, които университетите поставят към завършилите училище, са различни, а именно на по-високо ниво от изискванията на училищната програма. За живота в съвременното общество е много важно формирането на математически стил на мислене, проявяващ се в определени умствени умения. В процеса на решаване на задачи с модули е необходима способност за използване на техники като обобщение и спецификация, анализ, класификация и систематизация и аналогия. Решаването на такива задачи ви позволява да проверите знанията си за основните раздели на училищния курс, нивото на логическо мислене и първоначалните изследователски умения. Тази работа е посветена на един от разделите - решаване на уравнения, съдържащи модул. Състои се от три глави. Първата глава въвежда основните понятия и най-важните теоретични съображения. Втората глава предлага девет основни типа уравнения, съдържащи модул, обсъжда методите за решаването им и разглежда примери с различни нива на сложност. Третата глава предлага по-сложни и нестандартни уравнения (тригонометрични, експоненциални, логаритмични и ирационални). За всеки тип уравнение има упражнения за самостоятелно решаване (отговори и указания са приложени). Основната цел на тази работа е да предостави методическа помощ на учителите при подготовката за уроци и при организирането на избираеми курсове. Материалът може да се използва и като учебно помагало за ученици от гимназията. Задачите, предложени в работата, са интересни и не винаги лесни за решаване, което позволява да се направи по-съзнателна образователната мотивация на учениците, да се тестват техните способности и да се повиши нивото на подготовка на завършилите училище за постъпване в университети. Диференцираният подбор на предложените упражнения включва преход от репродуктивното ниво на овладяване на материала към творческото, както и възможността да научите как да прилагате знанията си при решаване на нестандартни проблеми.

Глава 1 Въведение.

Раздел 1. Определяне на абсолютна стойност .

Определение : Абсолютната стойност (модул) на реално число Анеотрицателно число се нарича: Аили -А. Обозначаване: │ А │ Записът гласи следното: „модул на числото a“ или „абсолютна стойност на числото a“

│ a, ако a > 0

│a│ = │ 0, ако a = 0 (1)

│ - и, ако a
Примери: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Разширяване на изразния модул:

a) │x - 8│, ако x > 12 b) │2x + 3│, ако x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

Раздел 2. Основни свойства.

Нека разгледаме основните свойства на абсолютната стойност. Свойство №1: Противоположните числа имат равни модули, т.е. │а│=│- а│Нека покажем, че равенството е правилно. Нека запишем определението на числото - А : │- а│= (2) Нека сравним комплекти (1) и (2). Очевидно е, че дефинициите на абсолютните стойности на числата АИ - Асъвпада. следователно │а│=│- а│
Когато разглеждаме следните свойства, ще се ограничим до тяхната формулировка, тъй като тяхното доказателство е дадено в Свойство №2: Абсолютната стойност на сумата от краен брой реални числа не надвишава сумата от абсолютните стойности на членовете: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Свойство #3: Абсолютната стойност на разликата между две реални числа не надвишава сумата от техните абсолютни стойности: │а - в│ ≤│а│+│в│ Имот #4: Абсолютната стойност на произведението на краен брой реални числа е равна на произведението на абсолютните стойности на факторите: │а·в│=│а│·│в│ Имот #5: Абсолютната стойност на частното на реалните числа е равна на частното на техните абсолютни стойности:

Раздел 3. Геометрична интерпретация на понятието модул на число.

Всяко реално число може да се свърже с точка от числовата ос, която ще бъде геометричен образ на това реално число. Всяка точка от числовата ос отговаря на разстоянието си от началото, т.е. дължината на отсечката от началото до дадена точка. Това разстояние винаги се счита за неотрицателна стойност. Следователно дължината на съответния сегмент ще бъде геометричната интерпретация на абсолютната стойност на дадено реално число

Представената геометрична илюстрация ясно потвърждава свойство No1, т.е. модулите на противоположните числа са равни. От тук лесно се разбира валидността на равенството: │х – а│= │а – x│. Решението на уравнението │х│= m, където m ≥ 0, а именно x 1,2 = ± m, също става по-очевидно. Примери: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
х 1,2 = 2; 4

Раздел 4. Графика на функцията y = │х│

Домейнът на тази функция е всички реални числа.

Раздел 5. Конвенции.

В бъдеще, когато се разглеждат примери за решаване на уравнения, ще се използват следните конвенции: ( - знак на системата [ - знак на съвкупността При решаване на система от уравнения (неравенства) се намира пресечната точка на решенията на уравненията (неравенствата), включени в системата. При решаване на система от уравнения (неравенства) се намира обединението на решенията, включени в системата от уравнения (неравенства).

Глава 2. Решаване на уравнения, съдържащи модул.

В тази глава ще разгледаме алгебрични методи за решаване на уравнения, съдържащи един или повече модули.

Раздел 1. Уравнения от вида │F (x)│= m

Уравнение от този тип се нарича най-просто. То има решение, ако и само ако m ≥ 0. По дефиниция на модула, оригиналното уравнение е еквивалентно на набор от две уравнения: │ Е(x)│=м
Примери:
№1. Решете уравнението: │7х - 2│= 9


Отговор: x 1 = - 1; х 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; х 2 = -3 Отговор: сумата от корените е - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 обозначават x 2 = m, m ≥ 0 x = 0; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – и двете стойности отговарят на условието m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Отговор: брой корени на уравнение 7. Упражнения:
№1. Решете уравнението и посочете сумата от корените: │х - 5│= 3 №2 . Решете уравнението и посочете по-малкия корен: │x 2 + x│= 0 №3 . Решете уравнението и посочете по-големия корен: │x 2 – 5x + 4│= 4 №4 .Решете уравнението и посочете целия корен: │2x 2 – 7x + 6│= 1 №5 .Решете уравнението и посочете броя на корените: │x 4 – 13x 2 + 50│= 14

Раздел 2. Уравнения от вида F(│х│) = m

Аргументът на функцията от лявата страна е под знака за модул, а дясната страна е независима от променливата. Нека разгледаме два начина за решаване на уравнения от този тип. 1 начин:По дефиниция на абсолютна стойност, оригиналното уравнение е еквивалентно на комбинацията от две системи. Във всяка от които е наложено условие за подмодулен израз. Е(│х│) =м
Тъй като функцията F(│x│) е четна в цялата област на дефиниция, корените на уравненията F(x) = m и F(- x) = m са двойки противоположни числа. Следователно е достатъчно да се реши една от системите (при разглеждане на примери по този начин ще бъде дадено решението на една система). Метод 2:Приложение на метода за въвеждане на нова променлива. В този случай се въвежда обозначението │x│= a, където a ≥ 0. Този метод е по-малко обемен като дизайн.
Примери: №1 . Решете уравнението: 3x 2 – 4│x│= - 1 Нека използваме въвеждането на нова променлива. Нека означим │x│= a, където a ≥ 0. Получаваме уравнението 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Връщане към първоначалната променлива: │ x│=1 и │х│= 1/3. Всяко уравнение има два корена. Отговор: x 1 = 1; х 2 = - 1; х 3 = 1 / 3 ; х 4 = - 1 / 3 . №2. Решете уравнението: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
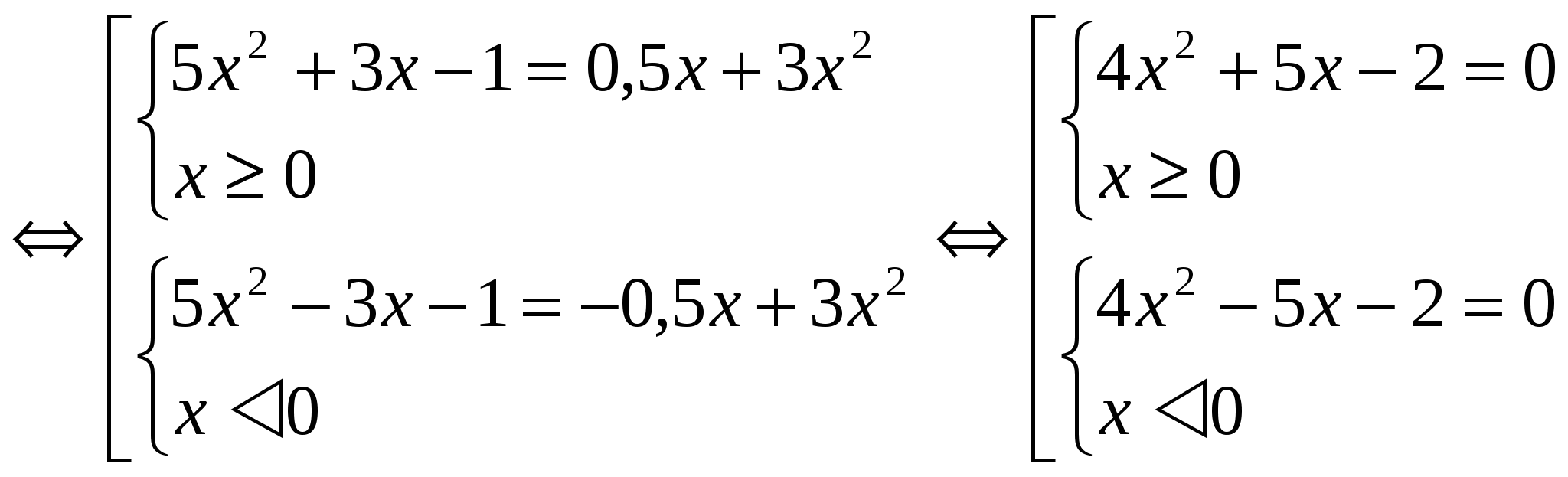Нека намерим решението на първата система от съвкупността: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Обърнете внимание, че x 2 не удовлетворява условието x ≥ 0. Решение втората система ще бъде числото, противоположно на стойността x 1. Отговор: x 1 = -5+√57 / 8 ; х 2 = 5-√57 / 8 .№3 . Решете уравнението: x 4 – │х│= 0 Нека означим │х│= a, където a ≥ 0. Получаваме уравнението a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Връщане към първоначалната променлива: │х│=0 и │х│= 1 x = 0; ± 1 Отговор: x 1 = 0; х 2 = 1; х 3 = - 1.
Упражнения: №6. Решете уравнението: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Решете уравнението, посочете броя на корените във вашия отговор: 3x 2 - 7│x│ + 2 = 0 №8 . Решете уравнението, посочете цели числа в отговора си: x 4 + │x│ - 2 = 0

Раздел 3. Уравнения от вида │F(x)│ = G(x)

Дясната страна на уравнение от този тип зависи от променлива и следователно има решение тогава и само ако дясната страна е функция G(x) ≥ 0. Оригиналното уравнение може да бъде решено по два начина : 1 начин:Стандарт, базиран на разкриването на модул въз основа на неговата дефиниция и се състои от еквивалентен преход към комбинация от две системи. │ Е(x)│ =Ж(Х)

Този метод може да се използва рационално в случай на сложен израз за функцията G(x) и по-малко сложен за функцията F(x), тъй като се предполага, че ще бъдат решени неравенства с функцията F(x). Метод 2:Състои се в прехода към еквивалентна система, при която условие е наложено от дясната страна. │ Е(х)│= Ж(х)

Този метод е по-удобен за използване, ако изразът за функцията G(x) е по-малко сложен, отколкото за функцията F(x), тъй като се приема решението на неравенството G(x) ≥ 0. Освен това в случая от няколко модула, препоръчително е да използвате втория вариант. Примери: №1. Решете уравнението: │x + 2│= 6 -2x
(1 начин) Отговор: x = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(x + 1)
(2 начина) Отговор: Произведението на корените е 3.
№3. Решете уравнението и посочете сумата от корените в отговора си:
│x - 6│= x 2 - 5x + 9

Отговор: сборът на корените е 4.
Упражнения: №9. │x + 4│= - 3x №10. Решете уравнението, посочете броя на решенията във вашия отговор:│x 2 + x - 1│= 2x – 1 №11 . Решете уравнението, посочете произведението на корените във вашия отговор:│x + 3│= x 2 + x – 6

Раздел 4. Уравнения от формата │F(x)│= F(x) и │F(x)│= - F(x)

Уравнения от този тип понякога се наричат ​​„най-красивите“. Тъй като дясната страна на уравненията зависи от променливата, решения съществуват тогава и само ако дясната страна е неотрицателна. Следователно оригиналните уравнения са еквивалентни на неравенствата:
│F(x)│= F(x) F(x) ≥ 0 и │F(x)│= - F(x) F(x) Примери: №1 . Решете уравнението, посочете по-малкия корен от цяло число във вашия отговор: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Отговор: x = 1№2. Решете уравнението, посочете дължината на интервала във вашия отговор: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Отговор: дължината на интервала е 6.№3 . Решете уравнението и посочете броя на целочислените решения във вашия отговор: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Отговор: 4 цели решения.№4 . Решете уравнението и посочете най-големия корен в отговора си:
│4 – x -
│= 4 – x –
x 2 – 5x + 5 = 0 D = 5 x 1,2 =
≈ 1,4

Отговор: x = 3.

Упражнения: №12. Решете уравнението, посочете целия корен в отговора си: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Решете уравнението, посочете броя на целочислените решения във вашия отговор: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Решете уравнението; в отговора си посочете цяло число, което не е коренът на уравнението:

Раздел 5. Уравнения от вида │F(x)│= │G(x)│

Тъй като и двете страни на уравнението са неотрицателни, решението включва разглеждане на два случая: субмодулните изрази са равни или противоположни по знак. Следователно първоначалното уравнение е еквивалентно на комбинацията от две уравнения: │ Е(х)│= │ Ж(х)│
Примери: №1. Решете уравнението, посочете целия корен в отговора си: │x + 3│=│2x - 1│
Отговор: цял корен x = 4.№2. Решете уравнението: │ x – x 2 - 1│=│2x – 3 – x 2 │
Отговор: x = 2.№3 . Решете уравнението и посочете произведението на корените във вашия отговор:




Корени на уравнения 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Отговор: произведението на корените е – 0,25. Упражнения: №15 . Решете уравнението и посочете цялото решение в отговора си: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Решете уравнението, посочете по-малкия корен в отговора си:│5x - 3│=│7 - x│ №17 . Решете уравнението и посочете сумата от корените в отговора си:

Раздел 6. Примери за решаване на нестандартни уравнения

В този раздел ще разгледаме примери за нестандартни уравнения, при решаването на които абсолютната стойност на израза се разкрива по дефиниция. Примери:

№1. Решете уравнението, посочете сумата от корените във вашия отговор: x · │x│- 5x – 6 = 0
Отговор: сборът на корените е 1 №2. . Решете уравнението, посочете по-малкия корен в отговора си: x 2 - 4x ·
- 5 = 0
Отговор: по-малък корен x = - 5. №3. Решете уравнението:

Отговор: x = -1. Упражнения: №18. Решете уравнението и посочете сумата от корените: x · │3x + 5│= 3x 2 + 4x + 3
№19. Решете уравнението: x 2 – 3x =

№20. Решете уравнението:

Раздел 7. Уравнения от вида │F(x)│+│G(x)│=0

Лесно се забелязва, че от лявата страна на уравнението от този тип е сумата от неотрицателни величини. Следователно първоначалното уравнение има решение тогава и само ако и двата члена са равни на нула едновременно. Уравнението е еквивалентно на системата от уравнения: │ Е(х)│+│ Ж(х)│=0
Примери: №1 . Решете уравнението:
Отговор: x = 2. №2. Решете уравнението: Отговор: x = 1. Упражнения: №21. Решете уравнението: №22 . Решете уравнението и посочете сумата от корените в отговора си: №23 . Решете уравнението и посочете броя на решенията във вашия отговор:

Раздел 8. Уравнения от формата │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

За решаване на уравнения от този тип се използва методът на интервалите. Ако го решим чрез последователно разширяване на модули, получаваме ннабори от системи, което е много тромаво и неудобно. Нека разгледаме алгоритъма на интервалния метод: 1). Намерете стойности на променливи х, за които всеки модул е ​​равен на нула (нули на подмодулни изрази):
2). Маркирайте намерените стойности на числова линия, която е разделена на интервали (броят на интервалите е съответно равен на н+1 ) 3). Определете с какъв знак се разкрива всеки модул на всеки от получените интервали (когато правите решение, можете да използвате числова линия, като маркирате знаците върху нея) 4). Първоначалното уравнение е еквивалентно на съвкупността н+1 системи, във всяка от които е посочена принадлежността на променливата хедин от интервалите. Примери: №1 . Решете уравнението и посочете най-големия корен в отговора си:
1). Да намерим нулите на подмодулните изрази: x = 2; x = -3 2). Нека маркираме намерените стойности на числовата линия и да определим с какъв знак се разкрива всеки модул на получените интервали:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- няма решения Уравнението има два корена. Отговор: най-големият корен x = 2. №2. Решете уравнението и дайте целия корен в отговора си:
1). Да намерим нулите на подмодулните изрази: x = 1,5; x = - 1 2). Нека маркираме намерените стойности на числовата линия и да определим с какъв знак се разкрива всеки модул на получените интервали: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
Последната система няма решения, следователно уравнението има два корена. Когато решавате уравнението, трябва да обърнете внимание на знака „-“ пред втория модул. Отговор: цял корен x = 7. №3. Решете уравнението, посочете сумата от корените във вашия отговор: 1). Да намерим нулите на подмодулните изрази: x = 5; х = 1; x = - 2 2). Нека маркираме намерените стойности на числовата линия и да определим с какъв знак се разкрива всеки модул в получените интервали: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Уравнението има два корена x = 0 и 2. Отговор: сборът на корените е 2. №4 . Решете уравнението: 1). Да намерим нулите на подмодулните изрази: x = 1; х = 2; x = 3. 2). Нека определим с какъв знак се разкрива всеки модул на получените интервали. 3).
Нека комбинираме решенията на първите три системи. Отговор: ; х = 5.
Упражнения: №24. Решете уравнението:
№25. Решете уравнението и посочете сумата от корените в отговора си: №26. Решете уравнението и посочете по-малкия корен в отговора си: №27. Решете уравнението и посочете по-големия корен в отговора си:

Раздел 9. Уравнения, съдържащи няколко модула

Уравненията, съдържащи множество модули, предполагат наличието на абсолютни стойности в подмодулни изрази. Основният принцип за решаване на уравнения от този тип е последователното разкриване на модули, като се започне от „външния“. По време на решението се използват техниките, разгледани в раздели № 1, № 3.

Примери: №1. Решете уравнението:
Отговор: x = 1; - единадесет. №2. Решете уравнението:
Отговор: x = 0; 4; - 4. №3. Решете уравнението и посочете произведението на корените във вашия отговор:
Отговор: произведението на корените е – 8. №4. Решете уравнението:
Нека обозначим уравненията на съвкупността (1) И (2) и разгледайте решението на всеки от тях поотделно за по-лесно проектиране. Тъй като и двете уравнения съдържат повече от един модул, по-удобно е да се извърши еквивалентен преход към набори от системи. (1)

(2)


Отговор:
Упражнения: №36. Решете уравнението, посочете сумата от корените в отговора си: 5 │3x-5│ = 25 x №37. Решете уравнението, ако има повече от един корен, посочете сумата от корените в отговора си: │x + 2│ x – 3x – 10 = 1 №38. Решете уравнението: 3 │2x -4│ = 9 │x│ №39. Решете уравнението и посочете броя на корените във вашия отговор: 2 │ sin x│ = √2 №40 . Решете уравнението и посочете броя на корените във вашия отговор:

Раздел 3. Логаритмични уравнения.

Преди да решите следните уравнения, е необходимо да прегледате свойствата на логаритмите и логаритмичната функция. Примери: №1. Решете уравнението, посочете произведението на корените във вашия отговор: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Случай 1: ако x ≥ - 1, тогава log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – удовлетворява условието x ≥ - 1 2 случай: ако x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – удовлетворява условието x - 1
Отговор: произведението на корените е – 15.
№2. Решете уравнението, посочете сумата от корените във вашия отговор: lg
О.Д.З.

Отговор: сумата от корените е 0,5.
№3. Решете уравнението: log 5
О.Д.З.

Отговор: x = 9. №4. Решете уравнението: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Нека използваме формулата за преместване към друга база. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Да намерим нулите на подмодулните изрази: x = 25; x = Тези числа разделят диапазона от приемливи стойности на три интервала, така че уравнението е еквивалентно на набор от три системи.
Отговор: )