Gleichungen und Ungleichungen mit Modul lösen bereitet oft Schwierigkeiten. Wenn Sie jedoch gut verstehen, was es ist der absolute Wert einer Zahl, Und wie man Ausdrücke, die ein Modulzeichen enthalten, korrekt erweitert, dann die Präsenz in der Gleichung Ausdruck unter dem Modulzeichen, stellt kein Hindernis mehr für seine Lösung dar.

Eine kleine Theorie. Jede Zahl hat zwei Eigenschaften: den absoluten Wert der Zahl und ihr Vorzeichen.

Beispielsweise hat die Zahl +5, oder einfach 5, ein „+“-Zeichen und einen absoluten Wert von 5.

Die Zahl -5 hat ein „-“-Zeichen und einen absoluten Wert von 5.

Die absoluten Werte der Zahlen 5 und -5 sind 5.

Der Absolutwert einer Zahl x wird Modul der Zahl genannt und mit |x| bezeichnet.

Wie wir sehen, ist der Modul einer Zahl gleich der Zahl selbst, wenn diese Zahl größer oder gleich Null ist, und dieser Zahl mit dem umgekehrten Vorzeichen, wenn diese Zahl negativ ist.

Das Gleiche gilt für alle Ausdrücke, die unter dem Modulzeichen stehen.

Die Modulerweiterungsregel sieht folgendermaßen aus:

|f(x)|= f(x) wenn f(x) ≥ 0, und

|f(x)|= - f(x), wenn f(x)< 0

Zum Beispiel |x-3|=x-3, wenn x-3≥0 und |x-3|=-(x-3)=3-x, wenn x-3<0.

Um eine Gleichung zu lösen, die einen Ausdruck unter dem Modulzeichen enthält, müssen Sie zuerst Erweitern Sie ein Modul gemäß der Modulerweiterungsregel.

Dann wird unsere Gleichung oder Ungleichung in zwei verschiedene Gleichungen, die auf zwei verschiedenen numerischen Intervallen existieren.

Eine Gleichung existiert in einem numerischen Intervall, in dem der Ausdruck unter dem Modulzeichen nicht negativ ist.

Und die zweite Gleichung existiert in dem Intervall, in dem der Ausdruck unter dem Modulzeichen negativ ist.

Schauen wir uns ein einfaches Beispiel an.

Lösen wir die Gleichung:

|x-3|=-x 2 +4x-3

1. Öffnen wir das Modul.

|x-3|=x-3, wenn x-3≥0, d.h. wenn x≥3

|x-3|=-(x-3)=3-x wenn x-3<0, т.е. если х<3

2. Wir haben zwei numerische Intervalle erhalten: x≥3 und x<3.

Betrachten wir, in welche Gleichungen die ursprüngliche Gleichung in jedem Intervall umgewandelt wird:

A) Für x≥3 |x-3|=x-3 und unsere Verwundung hat die Form:

Aufmerksamkeit! Diese Gleichung existiert nur auf dem Intervall x≥3!

Öffnen wir die Klammern und präsentieren wir ähnliche Begriffe:

und löse diese Gleichung.

Diese Gleichung hat Wurzeln:

x 1 =0, x 2 =3

Aufmerksamkeit! Da die Gleichung x-3=-x 2 +4x-3 nur auf dem Intervall x≥3 existiert, interessieren uns nur die Wurzeln, die zu diesem Intervall gehören. Diese Bedingung wird nur von x 2 =3 erfüllt.

B) Bei x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

Aufmerksamkeit! Diese Gleichung existiert nur auf dem Intervall x<3!

Öffnen wir die Klammern und präsentieren wir ähnliche Begriffe. Wir erhalten die Gleichung:

x 1 =2, x 2 =3

Aufmerksamkeit! da die Gleichung 3-x=-x 2 +4x-3 nur auf dem Intervall x existiert<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

Also: Aus dem ersten Intervall nehmen wir nur die Wurzel x=3, aus dem zweiten - die Wurzel x=2.

Der Modul ist der absolute Wert des Ausdrucks. Um ein Modul irgendwie zu kennzeichnen, ist es üblich, gerade Klammern zu verwenden. Der in gerade Klammern eingeschlossene Wert ist der Modulo-Wert. Der Prozess zum Lösen eines Moduls besteht darin, genau diese geraden Klammern zu öffnen, die in der mathematischen Sprache modulare Klammern genannt werden. Ihre Offenlegung erfolgt nach einer Reihe von Regeln. Außerdem werden in der Reihenfolge der Lösung der Module die Wertemengen der Ausdrücke gefunden, die in den modularen Klammern standen. In den meisten Fällen wird der Modul so erweitert, dass der Ausdruck, der submodular war, sowohl positive als auch negative Werte erhält, einschließlich des Wertes Null. Geht man von den festgelegten Eigenschaften des Moduls aus, so werden dabei verschiedene Gleichungen bzw. Ungleichungen aus dem Originalausdruck zusammengestellt, die dann gelöst werden müssen. Lassen Sie uns herausfinden, wie man Module löst.

Lösungsprozess

Das Lösen eines Moduls beginnt mit dem Schreiben der ursprünglichen Gleichung mit dem Modul. Um die Frage zu beantworten, wie man Gleichungen mit einem Modul löst, müssen Sie es vollständig öffnen. Um eine solche Gleichung zu lösen, wird das Modul erweitert. Alle modularen Ausdrücke müssen berücksichtigt werden. Es muss ermittelt werden, bei welchen Werten der in seiner Zusammensetzung enthaltenen unbekannten Größen der modulare Ausdruck in Klammern Null wird. Dazu reicht es aus, den Ausdruck in modularen Klammern mit Null gleichzusetzen und dann die Lösung der resultierenden Gleichung zu berechnen. Die gefundenen Werte müssen protokolliert werden. Auf die gleiche Weise müssen Sie auch den Wert aller unbekannten Variablen für alle Module in dieser Gleichung bestimmen. Als nächstes müssen Sie damit beginnen, alle Fälle der Existenz von Variablen in Ausdrücken zu definieren und zu berücksichtigen, wenn sie sich vom Wert Null unterscheiden. Dazu müssen Sie ein Ungleichungssystem aufschreiben, das allen Modulen der ursprünglichen Ungleichung entspricht. Ungleichungen müssen so geschrieben werden, dass sie alle verfügbaren und möglichen Werte für eine Variable abdecken, die auf dem Zahlenstrahl gefunden werden. Anschließend müssen Sie zur Visualisierung dieselbe Zahlenlinie zeichnen, auf der Sie später alle erhaltenen Werte grafisch darstellen können.

Mittlerweile lässt sich fast alles über das Internet erledigen. Das Modul ist keine Ausnahme von der Regel. Sie können es online auf einer der vielen modernen Ressourcen lösen. Alle Werte der Variablen, die im Nullmodul liegen, stellen eine spezielle Einschränkung dar, die bei der Lösung der Modulgleichung verwendet wird. In der ursprünglichen Gleichung müssen Sie alle verfügbaren modularen Klammern öffnen und gleichzeitig das Vorzeichen des Ausdrucks ändern, damit die Werte der gewünschten Variablen mit den Werten übereinstimmen, die auf dem Zahlenstrahl sichtbar sind. Die resultierende Gleichung muss gelöst werden. Der Wert der Variablen, der beim Lösen der Gleichung erhalten wird, muss anhand der vom Modul selbst festgelegten Begrenzung überprüft werden. Wenn der Wert der Variablen die Bedingung vollständig erfüllt, ist er korrekt. Alle Wurzeln, die bei der Lösung der Gleichung erhalten werden, aber nicht den Einschränkungen entsprechen, müssen verworfen werden.

MBOU-Sekundarschule Nr. 17, Ivanovo

« Gleichungen mit Modul
Methodische Entwicklung

Zusammengestellt

Mathelehrer

Lebedeva N.V.

20010

Erläuterungen

Kapitel 1 Einleitung

Abschnitt 2. Grundlegende Eigenschaften Abschnitt 3. Geometrische Interpretation des Konzepts des Moduls einer Zahl Abschnitt 4. Graph der Funktion y = |x| Abschnitt 5. Konventionen

Kapitel 2. Gleichungen lösen, die einen Modul enthalten

Abschnitt 1. Gleichungen der Form |F(x)| = m (am einfachsten) Abschnitt 2. Gleichungen der Form F(|x|) = m Abschnitt 3. Gleichungen der Form |F(x)| = G(x) Abschnitt 4. Gleichungen der Form |F(x)| = ± F(x) (am schönsten) Abschnitt 5. Gleichungen der Form |F(x)| = |G(x)| Abschnitt 6. Beispiele für die Lösung nicht standardmäßiger Gleichungen Abschnitt 7. Gleichungen der Form |F(x)| + |G(x)| = 0 Abschnitt 8. Gleichungen der Form |a 1 x ± b 1 | ± |a 2 x ± in 2 | ± …|a n x ± in n | = m Abschnitt 9. Gleichungen, die mehrere Module enthalten

Kapitel 3. Beispiele für die Lösung verschiedener Gleichungen mit Modul.

Abschnitt 1. Trigonometrische Gleichungen Abschnitt 2. Exponentialgleichungen Abschnitt 3. Logarithmische Gleichungen Abschnitt 4. Irrationale Gleichungen Abschnitt 5. Erweiterte Aufgaben Antworten zu den Übungen Referenzliste

Erläuterungen.

Der Begriff des Absolutwerts (Modul) einer reellen Zahl ist eines ihrer wesentlichen Merkmale. Dieses Konzept ist in verschiedenen Bereichen der physikalischen, mathematischen und technischen Wissenschaften weit verbreitet. In der Praxis des Mathematikunterrichts an weiterführenden Schulen gemäß dem Programm des Verteidigungsministeriums der Russischen Föderation wird der Begriff des „absoluten Wertes einer Zahl“ immer wieder angetroffen: In der 6. Klasse wird die Definition eines Moduls und seine geometrische Bedeutung wird vorgestellt; in der 8. Klasse wird der Begriff des absoluten Fehlers gebildet, die Lösung der einfachsten Gleichungen und Ungleichungen, die einen Modul enthalten, betrachtet und die Eigenschaften der arithmetischen Quadratwurzel untersucht; in der 11. Klasse findet sich das Konzept im Abschnitt „Wurzel N-ten Grades.“ Die Lehrerfahrung zeigt, dass Studierende bei der Lösung von Aufgaben, die Kenntnisse über diesen Stoff erfordern, häufig auf Schwierigkeiten stoßen und diese häufig überspringen, ohne mit der Bearbeitung begonnen zu haben. Ähnliche Aufgaben finden sich auch in den Texten der Prüfungsaufgaben für die Kurse der 9. und 11. Klasse. Darüber hinaus sind die Anforderungen, die Hochschulen an Schulabsolventen stellen, anders und zwar auf einem höheren Niveau als die Anforderungen des schulischen Lehrplans. Für das Leben in der modernen Gesellschaft ist die Ausbildung eines mathematischen Denkstils, der sich in bestimmten geistigen Fähigkeiten manifestiert, sehr wichtig. Bei der Lösung von Problemen mit Modulen ist die Fähigkeit erforderlich, Techniken wie Generalisierung und Spezifikation, Analyse, Klassifizierung und Systematisierung sowie Analogie anzuwenden. Durch die Lösung solcher Aufgaben können Sie Ihr Wissen über die Hauptabschnitte des Schulkurses, das Niveau des logischen Denkens und erste Recherchefähigkeiten testen. Diese Arbeit ist einem der Abschnitte gewidmet – dem Lösen von Gleichungen, die ein Modul enthalten. Es besteht aus drei Kapiteln. Im ersten Kapitel werden grundlegende Konzepte und die wichtigsten theoretischen Überlegungen vorgestellt. Das zweite Kapitel stellt neun Haupttypen von Gleichungen vor, die ein Modul enthalten, diskutiert Methoden zu deren Lösung und untersucht Beispiele unterschiedlicher Komplexität. Das dritte Kapitel bietet komplexere und nicht standardmäßige Gleichungen (trigonometrisch, exponentiell, logarithmisch und irrational). Für jeden Gleichungstyp gibt es Übungen zum eigenständigen Lösen (Lösungen und Anleitungen liegen bei). Der Hauptzweck dieser Arbeit besteht darin, Lehrkräften methodische Unterstützung bei der Unterrichtsvorbereitung und der Organisation von Wahlfächern zu bieten. Das Material kann auch als Lehrmittel für Oberstufenschüler verwendet werden. Die in der Arbeit vorgeschlagenen Aufgaben sind interessant und nicht immer leicht zu lösen, was es ermöglicht, die Bildungsmotivation der Schüler bewusster zu machen, ihre Fähigkeiten zu testen und den Grad der Vorbereitung der Schulabsolventen auf den Hochschulzugang zu erhöhen. Eine differenzierte Auswahl der vorgeschlagenen Übungen beinhaltet den Übergang von der reproduktiven Ebene der Beherrschung des Stoffes zur kreativen Ebene sowie die Möglichkeit, die Anwendung Ihres Wissens bei der Lösung nicht standardmäßiger Probleme zu lehren.

Kapitel 1 Einleitung.

Abschnitt 1. Bestimmung des Absolutwerts .

Definition : Der absolute Wert (Modul) einer reellen Zahl A eine nicht negative Zahl heißt: A oder -A. Bezeichnung: │ A │ Der Eintrag lautet wie folgt: „Modul der Zahl a“ oder „Absolutwert der Zahl a“

│ a, wenn a > 0

│a│ = │ 0, wenn a = 0 (1)

│ - und, wenn a
Beispiele: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Ausdrucksmodul erweitern:

a) │x - 8│, wenn x > 12 b) │2x + 3│, wenn x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

Abschnitt 2. Grundlegende Eigenschaften.

Betrachten wir die grundlegenden Eigenschaften des absoluten Wertes. Eigenschaft Nr. 1: Gegenüberliegende Zahlen haben gleiche Module, d.h. │а│=│- à│ Zeigen wir, dass die Gleichheit wahr ist. Schreiben wir die Definition der Zahl auf - A : │- a│= (2) Vergleichen wir die Sätze (1) und (2). Offensichtlich sind die Definitionen der Absolutwerte von Zahlen A Und - A zusammenpassen. Somit, │а│=│- à│
Bei der Betrachtung der folgenden Eigenschaften beschränken wir uns auf deren Formulierung, da ihr Beweis in angegeben ist Eigenschaft Nr. 2: Der Absolutwert der Summe einer endlichen Anzahl reeller Zahlen überschreitet nicht die Summe der Absolutwerte der Terme: │а 1 + à 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Eigenschaft Nr. 3: Der Absolutwert der Differenz zwischen zwei reellen Zahlen überschreitet nicht die Summe ihrer Absolutwerte: │а - в│ ≤│а│+│в│ Eigenschaft Nr. 4: Der Absolutwert des Produkts einer endlichen Anzahl reeller Zahlen ist gleich dem Produkt der Absolutwerte der Faktoren: │а·в│=│а│·│в│ Eigenschaft Nr. 5: Der Absolutwert des Quotienten der reellen Zahlen ist gleich dem Quotienten ihrer Absolutwerte:

Abschnitt 3. Geometrische Interpretation des Konzepts des Moduls einer Zahl.

Jede reelle Zahl kann einem Punkt auf der Zahlenlinie zugeordnet werden, der ein geometrisches Abbild dieser reellen Zahl darstellt. Jeder Punkt auf der Zahlenlinie entspricht seinem Abstand vom Ursprung, d. h. die Länge des Segments vom Ursprung bis zu einem bestimmten Punkt. Dieser Abstand wird immer als nicht negativer Wert betrachtet. Daher ist die Länge des entsprechenden Segments die geometrische Interpretation des Absolutwerts einer bestimmten reellen Zahl

Die vorgestellte geometrische Darstellung bestätigt eindeutig Eigenschaft Nr. 1, d.h. die Moduli entgegengesetzter Zahlen sind gleich. Von hier aus ist die Gültigkeit der Gleichheit leicht zu verstehen: │х – а│= │а – x│. Auch die Lösung der Gleichung │х│= m mit m ≥ 0, nämlich x 1,2 = ± m, wird deutlicher. Beispiele: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; 4

Abschnitt 4. Graph der Funktion y = │х│

Der Definitionsbereich dieser Funktion sind alle reellen Zahlen.

Abschnitt 5. Konventionen.

In Zukunft werden bei der Betrachtung von Beispielen zur Lösung von Gleichungen die folgenden Konventionen verwendet: ( - Zeichen des Systems [ - Zeichen der Gesamtheit Beim Lösen eines Gleichungssystems (Ungleichungen) wird der Schnittpunkt der Lösungen der im System enthaltenen Gleichungen (Ungleichungen) ermittelt. Beim Lösen einer Menge von Gleichungen (Ungleichungen) wird die Vereinigung der in der Menge von Gleichungen (Ungleichungen) enthaltenen Lösungen gefunden.

Kapitel 2. Gleichungen lösen, die einen Modul enthalten.

In diesem Kapitel betrachten wir algebraische Methoden zum Lösen von Gleichungen, die ein oder mehrere Module enthalten.

Abschnitt 1. Gleichungen der Form │F (x)│= m

Eine Gleichung dieser Art nennt man die einfachste. Es gibt genau dann eine Lösung, wenn m ≥ 0. Nach Definition des Moduls entspricht die ursprüngliche Gleichung einem Satz von zwei Gleichungen: │ F(x)│=M
Beispiele:
№1. Lösen Sie die Gleichung: │7х - 2│= 9


Antwort: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Antwort: Die Summe der Wurzeln ist - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 bezeichnen wir x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5 m + 4 = 0 m = 1; 4 – beide Werte erfüllen die Bedingung m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Antwort: Anzahl der Wurzeln von Gleichung 7. Übungen:
№1. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln an: │х - 5│= 3 №2 . Lösen Sie die Gleichung und geben Sie die kleinere Wurzel an: │x 2 + x│= 0 №3 . Lösen Sie die Gleichung und geben Sie die größere Wurzel an: │x 2 – 5x + 4│= 4 №4 .Lösen Sie die Gleichung und geben Sie die ganze Wurzel an: │2x 2 – 7x + 6│= 1 №5 .Lösen Sie die Gleichung und geben Sie die Anzahl der Wurzeln an: │x 4 – 13x 2 + 50│= 14

Abschnitt 2. Gleichungen der Form F(│х│) = m

Das Funktionsargument auf der linken Seite steht unter dem Modulzeichen und auf der rechten Seite ist es unabhängig von der Variablen. Betrachten wir zwei Möglichkeiten, Gleichungen dieser Art zu lösen. 1 Weg: Per Definition des Absolutwerts entspricht die ursprüngliche Gleichung der Kombination zweier Systeme. In jedem Fall wird einem submodularen Ausdruck eine Bedingung auferlegt. F(│х│) =M
Da die Funktion F(│x│) im gesamten Definitionsbereich gerade ist, sind die Wurzeln der Gleichungen F(x) = m und F(- x) = m Paare entgegengesetzter Zahlen. Daher reicht es aus, eines der Systeme zu lösen (bei der Betrachtung von Beispielen auf diese Weise wird die Lösung für ein System angegeben). Methode 2: Anwendung der Methode zur Einführung einer neuen Variablen. In diesem Fall wird die Bezeichnung │x│= a eingeführt, wobei a ≥ 0. Diese Methode ist weniger umfangreich im Design.
Beispiele: №1 . Lösen Sie die Gleichung: 3x 2 – 4│x│= - 1 Lassen Sie uns die Einführung einer neuen Variablen verwenden. Bezeichnen wir │x│= a, wobei a ≥ 0. Wir erhalten die Gleichung 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Zurück zur ursprünglichen Variablen: │ x│=1 und │х│= 1/3. Jede Gleichung hat zwei Wurzeln. Antwort: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Lösen Sie die Gleichung: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
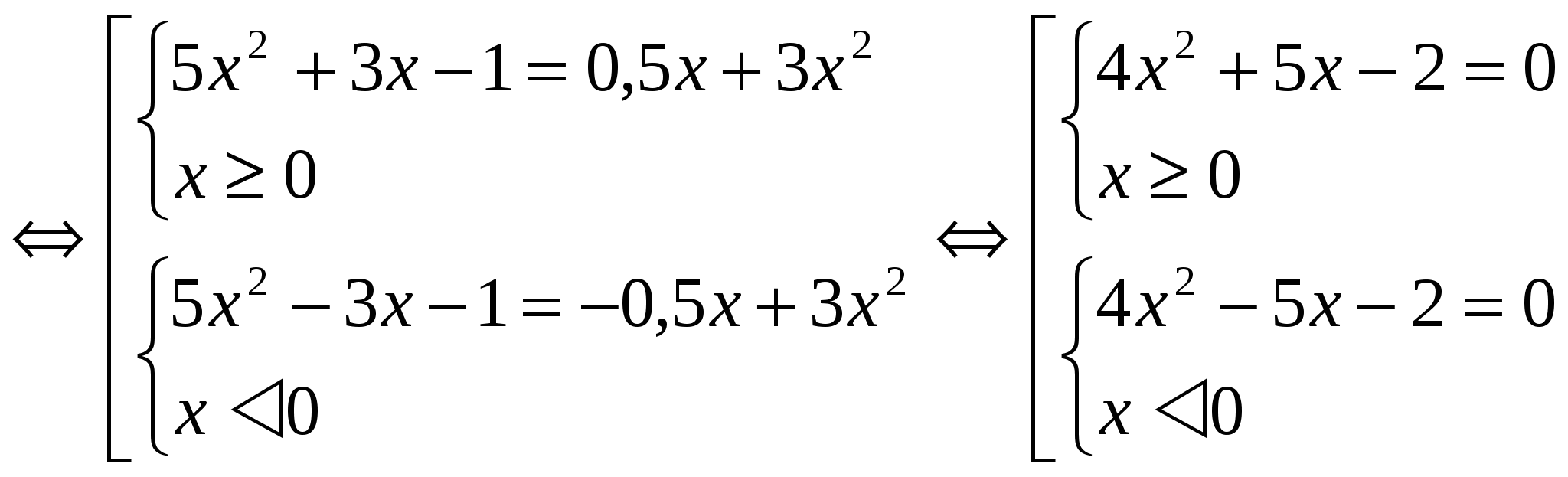Finden wir die Lösung für das erste System der Grundgesamtheit: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Beachten Sie, dass x 2 nicht erfüllt die Bedingung x ≥ 0. Lösung Das zweite System wird die Zahl sein, die dem Wert x 1 entgegengesetzt ist. Antwort: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Lösen Sie die Gleichung: x 4 – │х│= 0 Bezeichnen wir │х│= a, wobei a ≥ 0. Wir erhalten die Gleichung a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Rückkehr zur ursprünglichen Variablen: │х│=0 und │х│= 1 x = 0; ± 1 Antwort: x 1 = 0; X 2 = 1; X 3 = - 1.
Übungen: №6. Lösen Sie die Gleichung: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Lösen Sie die Gleichung und geben Sie die Anzahl der Wurzeln in Ihrer Antwort an: 3x 2 - 7│x│ + 2 = 0 №8 . Lösen Sie die Gleichung und geben Sie in Ihrer Antwort ganzzahlige Lösungen an: x 4 + │x│ - 2 = 0

Abschnitt 3. Gleichungen der Form │F(x)│ = G(x)

Die rechte Seite einer solchen Gleichung hängt von einer Variablen ab und hat daher genau dann eine Lösung, wenn die rechte Seite eine Funktion G(x) ≥ 0 ist. Die ursprüngliche Gleichung kann auf zwei Arten gelöst werden : 1 Weg: Standard, der auf der Offenlegung eines Moduls basierend auf seiner Definition basiert und aus einem gleichwertigen Übergang zu einer Kombination zweier Systeme besteht. │ F(x)│ =G(X)

Diese Methode kann bei einem komplexen Ausdruck für die Funktion G(x) und einem weniger komplexen Ausdruck für die Funktion F(x) sinnvoll angewendet werden, da davon ausgegangen wird, dass Ungleichungen mit der Funktion F(x) gelöst werden. Methode 2: Besteht im Übergang zu einem äquivalenten System, in dem auf der rechten Seite eine Bedingung gestellt wird. │ F(X)│= G(X)

Diese Methode ist bequemer anzuwenden, wenn der Ausdruck für die Funktion G(x) weniger komplex ist als für die Funktion F(x), da die Lösung der Ungleichung G(x) ≥ 0 angenommen wird. Darüber hinaus im Fall Bei mehreren Modulen empfiehlt es sich, die zweite Möglichkeit zu nutzen. Beispiele: №1. Lösen Sie die Gleichung: │x + 2│= 6 -2x
(1 Weg) Antwort: x = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(x + 1)
(2-Wege) Antwort: Das Produkt der Wurzeln ist 3.
№3. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an:
│x - 6│= x 2 - 5x + 9

Antwort: Die Summe der Wurzeln ist 4.
Übungen: №9. │x + 4│= - 3x №10. Lösen Sie die Gleichung und geben Sie die Anzahl der Lösungen in Ihrer Antwort an:│x 2 + x - 1│= 2x – 1 №11 . Lösen Sie die Gleichung und geben Sie das Produkt der Wurzeln in Ihrer Antwort an:│x + 3│= x 2 + x – 6

Abschnitt 4. Gleichungen der Form │F(x)│= F(x) und │F(x)│= - F(x)

Gleichungen dieser Art werden manchmal als „die schönsten“ bezeichnet. Da die rechte Seite der Gleichungen von der Variablen abhängt, gibt es genau dann Lösungen, wenn die rechte Seite nicht negativ ist. Daher sind die ursprünglichen Gleichungen äquivalent zu den Ungleichungen:
│F(x)│= F(x) F(x) ≥ 0 und │F(x)│= - F(x) F(x) Beispiele: №1 . Lösen Sie die Gleichung und geben Sie die kleinere ganzzahlige Wurzel in Ihrer Antwort an: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Antwort: x = 1№2. Lösen Sie die Gleichung und geben Sie die Länge des Intervalls in Ihrer Antwort an: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Antwort: Die Länge des Intervalls beträgt 6.№3 . Lösen Sie die Gleichung und geben Sie die Anzahl der ganzzahligen Lösungen in Ihrer Antwort an: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Antwort: 4 ganze Lösungen.№4 . Lösen Sie die Gleichung und geben Sie die größte Wurzel in Ihrer Antwort an:
│4 – x -
│= 4 – x –
x 2 – 5x + 5 = 0 D = 5 x 1,2 =
≈ 1,4

Antwort: x = 3.

Übungen: №12. Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die ganze Wurzel an: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Lösen Sie die Gleichung und geben Sie die Anzahl der ganzzahligen Lösungen in Ihrer Antwort an: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Lösen Sie die Gleichung. Geben Sie in Ihrer Antwort eine ganze Zahl an, die nicht die Wurzel der Gleichung ist:

Abschnitt 5. Gleichungen der Form │F(x)│= │G(x)│

Da beide Seiten der Gleichung nicht negativ sind, umfasst die Lösung die Betrachtung zweier Fälle: Submodulare Ausdrücke haben das gleiche oder entgegengesetzte Vorzeichen. Daher entspricht die ursprüngliche Gleichung der Kombination zweier Gleichungen: │ F(X)│= │ G(X)│
Beispiele: №1. Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die ganze Wurzel an: │x + 3│=│2x - 1│
Antwort: ganze Wurzel x = 4.№2. Löse die Gleichung: │ x – x 2 - 1│=│2x – 3 – x 2 │
Antwort: x = 2.№3 . Lösen Sie die Gleichung und geben Sie das Produkt der Wurzeln in Ihrer Antwort an:




Wurzelgleichungen 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Antwort: Das Produkt der Wurzeln ist – 0,25. Übungen: №15 . Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die gesamte Lösung an: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Lösen Sie die Gleichung und geben Sie die kleinere Wurzel in Ihrer Antwort an:│5x - 3│=│7 - x│ №17 . Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an:

Abschnitt 6. Beispiele für die Lösung nicht standardmäßiger Gleichungen

In diesem Abschnitt betrachten wir Beispiele für nicht standardmäßige Gleichungen, bei deren Lösung der Absolutwert des Ausdrucks per Definition ermittelt wird. Beispiele:

№1. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: x · │x│- 5x – 6 = 0
Antwort: Die Summe der Wurzeln ist 1 №2. . Lösen Sie die Gleichung und geben Sie die kleinere Wurzel in Ihrer Antwort an: x 2 - 4x ·
- 5 = 0
Antwort: kleinere Wurzel x = - 5. №3. Löse die Gleichung:

Antwort: x = -1. Übungen: №18. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln an: x · │3x + 5│= 3x 2 + 4x + 3
№19. Lösen Sie die Gleichung: x 2 – 3x =

№20. Löse die Gleichung:

Abschnitt 7. Gleichungen der Form │F(x)│+│G(x)│=0

Es ist leicht zu erkennen, dass auf der linken Seite einer Gleichung dieses Typs die Summe nichtnegativer Größen steht. Daher hat die ursprüngliche Gleichung genau dann eine Lösung, wenn beide Terme gleichzeitig gleich Null sind. Die Gleichung entspricht dem Gleichungssystem: │ F(X)│+│ G(X)│=0
Beispiele: №1 . Löse die Gleichung:
Antwort: x = 2. №2. Löse die Gleichung: Antwort: x = 1. Übungen: №21. Löse die Gleichung: №22 . Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: №23 . Lösen Sie die Gleichung und geben Sie die Anzahl der Lösungen in Ihrer Antwort an:

Abschnitt 8. Gleichungen der Form │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

Um Gleichungen dieser Art zu lösen, wird die Intervallmethode verwendet. Wenn wir es durch sequentielle Erweiterung von Modulen lösen, erhalten wir N von Systemen, was sehr umständlich und unpraktisch ist. Betrachten wir den Algorithmus der Intervallmethode: 1). Finden Sie Variablenwerte X, für die jedes Modul gleich Null ist (Nullen submodularer Ausdrücke):
2). Markieren Sie die gefundenen Werte auf einem Zahlenstrahl, der in Intervalle unterteilt ist (die Anzahl der Intervalle ist jeweils gleich). N+1 ) 3). Bestimmen Sie, mit welchem ​​Vorzeichen jedes Modul in jedem der resultierenden Intervalle angezeigt wird (beim Formulieren einer Lösung können Sie einen Zahlenstrahl verwenden und die Vorzeichen darauf markieren) 4). Die ursprüngliche Gleichung entspricht dem Aggregat N+1 Systeme, in denen jeweils die Zugehörigkeit der Variablen angegeben ist X eines der Intervalle. Beispiele: №1 . Lösen Sie die Gleichung und geben Sie die größte Wurzel in Ihrer Antwort an:
1). Finden wir die Nullstellen der submodularen Ausdrücke: x = 2; x = -3 2). Markieren wir die gefundenen Werte auf dem Zahlenstrahl und bestimmen wir, mit welchem ​​Vorzeichen jedes Modul in den erhaltenen Intervallen aufgedeckt wird:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- keine Lösungen Die Gleichung hat zwei Wurzeln. Antwort: Die größte Wurzel x = 2. №2. Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die ganze Wurzel an:
1). Finden wir die Nullstellen der submodularen Ausdrücke: x = 1,5; x = - 1 2). Markieren wir die gefundenen Werte auf dem Zahlenstrahl und bestimmen wir, mit welchem ​​Vorzeichen jedes Modul in den resultierenden Intervallen aufgedeckt wird: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
Das letzte System hat keine Lösungen, daher hat die Gleichung zwei Wurzeln. Beim Lösen der Gleichung sollten Sie auf das „-“-Zeichen vor dem zweiten Modul achten. Antwort: ganze Wurzel x = 7. №3. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: 1). Finden wir die Nullstellen der submodularen Ausdrücke: x = 5; x = 1; x = - 2 2). Markieren wir die gefundenen Werte auf dem Zahlenstrahl und bestimmen wir, mit welchem ​​Vorzeichen jedes Modul in den resultierenden Intervallen aufgedeckt wird: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Die Gleichung hat zwei Wurzeln x = 0 und 2. Antwort: Die Summe der Wurzeln ist 2. №4 . Lösen Sie die Gleichung: 1). Finden wir die Nullstellen der submodularen Ausdrücke: x = 1; x = 2; x = 3. 2). Lassen Sie uns bestimmen, mit welchem ​​Vorzeichen jedes Modul in den resultierenden Intervallen angezeigt wird. 3).
Kombinieren wir die Lösungen der ersten drei Systeme. Antwort: ; x = 5.
Übungen: №24. Löse die Gleichung:
№25. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: №26. Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die kleinere Wurzel an: №27. Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die größere Wurzel an:

Abschnitt 9. Gleichungen, die mehrere Module enthalten

Gleichungen, die mehrere Module enthalten, gehen davon aus, dass in submodularen Ausdrücken absolute Werte vorhanden sind. Das Grundprinzip zur Lösung derartiger Gleichungen ist die sequentielle Offenlegung von Modulen, beginnend mit dem „externen“. Bei der Lösung kommen die in den Abschnitten Nr. 1, Nr. 3 besprochenen Techniken zum Einsatz.

Beispiele: №1. Löse die Gleichung:
Antwort: x = 1; - elf. №2. Löse die Gleichung:
Antwort: x = 0; 4; - 4. №3. Lösen Sie die Gleichung und geben Sie das Produkt der Wurzeln in Ihrer Antwort an:
Antwort: Das Produkt der Wurzeln ist – 8. №4. Löse die Gleichung:
Bezeichnen wir die Gleichungen der Bevölkerung (1) Und (2) und überlegen Sie sich die Lösung für jedes davon separat, um das Design zu vereinfachen. Da beide Gleichungen mehr als ein Modul enthalten, ist es bequemer, einen äquivalenten Übergang zu Systemmengen durchzuführen. (1)

(2)


Antwort:
Übungen: №36. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: 5 │3x-5│ = 25 x №37. Lösen Sie die Gleichung. Wenn es mehr als eine Wurzel gibt, geben Sie die Summe der Wurzeln in Ihrer Antwort an: │x + 2│ x – 3x – 10 = 1 №38. Lösen Sie die Gleichung: 3 │2x -4│ = 9 │x│ №39. Lösen Sie die Gleichung und geben Sie die Anzahl der Wurzeln in Ihrer Antwort an: 2 │ sin x│ = √2 №40 . Lösen Sie die Gleichung und geben Sie die Anzahl der Wurzeln in Ihrer Antwort an:

Abschnitt 3. Logarithmische Gleichungen.

Bevor Sie die folgenden Gleichungen lösen, müssen Sie die Eigenschaften von Logarithmen und der logarithmischen Funktion überprüfen. Beispiele: №1. Lösen Sie die Gleichung und geben Sie das Produkt der Wurzeln in Ihrer Antwort an: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Fall 1: Wenn x ≥ - 1, dann log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – erfüllt die Bedingung x ≥ - 1 2 Fall: wenn x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – erfüllt die Bedingung x - 1
Antwort: Das Produkt der Wurzeln ist – 15.
№2. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: lg
O.D.Z.

Antwort: Die Summe der Wurzeln beträgt 0,5.
№3. Lösen Sie die Gleichung: log 5
O.D.Z.

Antwort: x = 9. №4. Lösen Sie die Gleichung: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Verwenden wir die Formel für den Übergang zu einer anderen Basis. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Finden wir die Nullstellen der submodularen Ausdrücke: x = 25; x = Diese Zahlen unterteilen den Bereich akzeptabler Werte in drei Intervalle, sodass die Gleichung einer Menge von drei Systemen entspricht.
Antwort: )