Résolution d'équations et d'inégalités avec module pose souvent des difficultés. Cependant, si vous comprenez bien ce que c'est la valeur absolue d'un nombre, Et comment développer correctement des expressions contenant un signe de module, alors la présence dans l'équation expression sous le signe du module, cesse d’être un obstacle à sa solution.

Un peu de théorie. Chaque nombre a deux caractéristiques : la valeur absolue du nombre et son signe.

Par exemple, le nombre +5, ou simplement 5, a un signe « + » et une valeur absolue de 5.

Le nombre -5 a un signe "-" et une valeur absolue de 5.

Les valeurs absolues des nombres 5 et -5 sont 5.

La valeur absolue d'un nombre x est appelée le module du nombre et est notée |x|.

Comme on le voit, le module d'un nombre est égal au nombre lui-même si ce nombre est supérieur ou égal à zéro, et à ce nombre de signe opposé si ce nombre est négatif.

Il en va de même pour toutes les expressions qui apparaissent sous le signe du module.

La règle d'expansion du module ressemble à ceci :

|f(x)|= f(x) si f(x) ≥ 0, et

|f(x)|= - f(x), si f(x)< 0

Par exemple |x-3|=x-3, si x-3≥0 et |x-3|=-(x-3)=3-x, si x-3<0.

Pour résoudre une équation contenant une expression sous le signe du module, il faut d'abord développer un module selon la règle d'expansion du module.

Alors notre équation ou inégalité devient en deux équations différentes existant sur deux intervalles numériques différents.

Il existe une équation sur un intervalle numérique sur lequel l'expression sous le signe du module est non négative.

Et la deuxième équation existe sur l'intervalle sur lequel l'expression sous le signe du module est négative.

Regardons un exemple simple.

Résolvons l'équation :

|x-3|=-x2 +4x-3

1. Ouvrons le module.

|x-3|=x-3, si x-3≥0, c'est-à-dire si x≥3

|x-3|=-(x-3)=3-x si x-3<0, т.е. если х<3

2. Nous avons reçu deux intervalles numériques : x≥3 et x<3.

Considérons dans quelles équations l'équation d'origine est transformée sur chaque intervalle :

A) Pour x≥3 |x-3|=x-3, et notre blessure a la forme :

Attention! Cette équation n'existe que sur l'intervalle x≥3 !

Ouvrons les parenthèses et présentons des termes similaires :

et résolvez cette équation.

Cette équation a des racines :

x1 =0, x2 =3

Attention! puisque l'équation x-3=-x 2 +4x-3 n'existe que sur l'intervalle x≥3, nous ne nous intéressons qu'aux racines qui appartiennent à cet intervalle. Cette condition n'est satisfaite que par x 2 =3.

B) À x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

Attention! Cette équation n'existe que sur l'intervalle x<3!

Ouvrons les parenthèses et présentons des termes similaires. On obtient l'équation :

x1 =2, x2 =3

Attention! puisque l'équation 3-x=-x 2 +4x-3 n'existe que sur l'intervalle x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

Donc : du premier intervalle nous prenons uniquement la racine x=3, du second - la racine x=2.

Le module est la valeur absolue de l'expression. Pour indiquer d'une manière ou d'une autre un module, il est d'usage d'utiliser des parenthèses droites. La valeur entre parenthèses paires est la valeur prise modulo. Le processus de résolution de n'importe quel module consiste à ouvrir ces parenthèses très droites, qui en langage mathématique sont appelées parenthèses modulaires. Leur divulgation s'effectue selon un certain nombre de règles. De plus, dans l'ordre de résolution des modules, on trouve les ensembles de valeurs des expressions qui se trouvaient entre parenthèses modulaires. Dans la plupart des cas, le module est étendu de telle sorte que l'expression qui était sous-modulaire reçoive à la fois des valeurs positives et négatives, y compris la valeur zéro. Si nous partons des propriétés établies du module, diverses équations ou inégalités de l'expression originale sont compilées au cours du processus, qui doivent ensuite être résolues. Voyons comment résoudre les modules.

Processus de résolution

La résolution d'un module commence par écrire l'équation originale avec le module. Pour répondre à la question de savoir comment résoudre des équations avec un module, vous devez l'ouvrir complètement. Pour résoudre une telle équation, le module est développé. Toutes les expressions modulaires doivent être prises en compte. Il est nécessaire de déterminer à quelles valeurs des quantités inconnues entrant dans sa composition, l'expression modulaire entre parenthèses devient nulle. Pour ce faire, il suffit d'assimiler l'expression entre parenthèses modulaires à zéro, puis de calculer la solution de l'équation résultante. Les valeurs trouvées doivent être enregistrées. De la même manière, vous devez également déterminer la valeur de toutes les variables inconnues pour tous les modules de cette équation. Ensuite, il faut déterminer et considérer tous les cas d'existence de variables dans les expressions lorsqu'elles sont différentes de la valeur zéro. Pour ce faire, vous devez écrire un système d'inégalités correspondant à tous les modules de l'inégalité d'origine. Les inégalités doivent être écrites de manière à couvrir toutes les valeurs disponibles et possibles pour une variable trouvées sur la droite numérique. Ensuite, vous devez tracer cette même droite numérique pour la visualisation, sur laquelle tracer ultérieurement toutes les valeurs obtenues.

Presque tout peut désormais se faire sur Internet. Le module ne déroge pas à la règle. Vous pouvez le résoudre en ligne sur l'une des nombreuses ressources modernes. Toutes les valeurs de la variable qui se trouvent dans le module zéro constitueront une contrainte spéciale qui sera utilisée dans le processus de résolution de l'équation modulaire. Dans l'équation originale, vous devez ouvrir toutes les parenthèses modulaires disponibles, tout en modifiant le signe de l'expression afin que les valeurs de la variable souhaitée coïncident avec les valeurs visibles sur la droite numérique. L'équation résultante doit être résolue. La valeur de la variable qui sera obtenue lors de la résolution de l'équation doit être vérifiée par rapport à la limitation spécifiée par le module lui-même. Si la valeur de la variable satisfait pleinement à la condition, alors elle est correcte. Toutes les racines qui seront obtenues lors de la résolution de l'équation, mais qui ne respecteront pas les restrictions, doivent être écartées.

Lycée MBOU n°17, Ivanovo

« Equations avec module"
Développement méthodologique

Compilé

prof de maths

Lebedeva N.V.

20010

Note explicative

Chapitre 1 Introduction

Section 2. Propriétés de base Section 3. Interprétation géométrique de la notion de module d'un nombre Section 4. Graphique de la fonction y = |x| Article 5. Conventions

Chapitre 2. Résolution d'équations contenant un module

Section 1. Équations de la forme |F(x)| = m (le plus simple) Section 2. Équations de la forme F(|x|) = m Section 3. Équations de la forme |F(x)| = G(x) Section 4. Équations de la forme |F(x)| = ± F(x) (le plus beau) Section 5. Équations de la forme |F(x)| = |G(x)| Section 6. Exemples de résolution d'équations non standard Section 7. Équations de la forme |F(x)| + |G(x)| = 0 Section 8. Équations de la forme |a 1 x ± b 1 | ± |une 2 x ± b 2 | ± …|a n x ± dans n | = m Section 9. Équations contenant plusieurs modules

Chapitre 3. Exemples de résolution de diverses équations avec module.

Section 1. Équations trigonométriques Section 2. Équations exponentielles Section 3. Équations logarithmiques Section 4. Équations irrationnelles Section 5. Tâches avancées Réponses aux exercices Bibliographie

Note explicative.

La notion de valeur absolue (module) d'un nombre réel est l'une de ses caractéristiques essentielles. Ce concept est répandu dans diverses sections des sciences physiques, mathématiques et techniques. Dans la pratique de l'enseignement des cours de mathématiques dans les écoles secondaires conformément au programme du ministère de la Défense de la Fédération de Russie, la notion de « valeur absolue d'un nombre » est rencontrée à plusieurs reprises : en 6e année, la définition d'un module et sa signification géométrique est introduite ; en 8e année, la notion d'erreur absolue est formée, la solution des équations et inégalités les plus simples contenant un module est envisagée et les propriétés de la racine carrée arithmétique sont étudiées ; en 11e, le concept se retrouve dans la section « Racine n-ème degré." L'expérience pédagogique montre que les étudiants rencontrent souvent des difficultés pour résoudre des tâches qui nécessitent la connaissance de cette matière, et les sautent souvent sans commencer à les terminer. Les textes des devoirs d'examen pour les cours de 9e et 11e années comprennent également des devoirs similaires. De plus, les exigences que les universités imposent aux diplômés des écoles sont différentes, à savoir à un niveau plus élevé que les exigences du programme scolaire. Pour la vie dans la société moderne, la formation d'un style de pensée mathématique, se manifestant par certaines compétences mentales, est très importante. Dans le processus de résolution de problèmes avec les modules, la capacité d'utiliser des techniques telles que la généralisation et la spécification, l'analyse, la classification et la systématisation, ainsi que l'analogie est requise. Résoudre de telles tâches vous permet de tester vos connaissances des principales sections du cours scolaire, votre niveau de pensée logique et vos compétences de recherche initiales. Ce travail est consacré à l'une des sections - résolution d'équations contenant un module. Il se compose de trois chapitres. Le premier chapitre présente les concepts de base et les considérations théoriques les plus importantes. Le deuxième chapitre propose neuf principaux types d'équations contenant un module, discute des méthodes pour les résoudre et examine des exemples de différents niveaux de complexité. Le troisième chapitre propose des équations plus complexes et non standards (trigonométriques, exponentielles, logarithmiques et irrationnelles). Pour chaque type d'équation, il existe des exercices de résolution indépendante (les réponses et les instructions sont jointes). L'objectif principal de ce travail est d'apporter une assistance méthodologique aux enseignants dans la préparation des cours et dans l'organisation des cours au choix. Le matériel peut également être utilisé comme support pédagogique pour les élèves du secondaire. Les tâches proposées dans l'ouvrage sont intéressantes et pas toujours faciles à résoudre, ce qui permet de rendre plus consciente la motivation éducative des étudiants, de tester leurs capacités et d'augmenter le niveau de préparation des bacheliers à l'entrée à l'université. Une sélection différenciée des exercices proposés implique un passage du niveau reproductif de maîtrise du matériel au niveau créatif, ainsi que la possibilité d'enseigner comment appliquer vos connaissances lors de la résolution de problèmes non standards.

Chapitre 1 Introduction.

Section 1. Détermination de la valeur absolue .

Définition : La valeur absolue (module) d'un nombre réel UN un nombre non négatif s'appelle : UN ou -UN. Désignation: │ UN │ L'entrée se lit comme suit : « module du nombre a » ou « valeur absolue du nombre a »

│ une, si une > 0

│a│ = │ 0, si a = 0 (1)

│ - et, si un
Exemples: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Développez le module d'expression :

a) │x - 8│, si x > 12 b) │2x + 3│, si x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

Section 2. Propriétés de base.

Considérons les propriétés fondamentales de la valeur absolue. Propriété n°1 : Les nombres opposés ont des modules égaux, c'est-à-dire │а│=│- а│ Montrons que l'égalité est vraie. Écrivons la définition du nombre - UN : │- un│= (2) Comparons les ensembles (1) et (2). Évidemment, les définitions des valeurs absolues des nombres UN Et - UN correspondre. Ainsi, │а│=│- а│
En considérant les propriétés suivantes, nous nous limiterons à leur formulation, puisque leur preuve est donnée dans Propriété n°2 : La valeur absolue de la somme d'un nombre fini de nombres réels ne dépasse pas la somme des valeurs absolues des termes : │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Propriété n°3 : La valeur absolue de la différence entre deux nombres réels ne dépasse pas la somme de leurs valeurs absolues : │а - в│ ≤│а│+│в│ Propriété n°4 : La valeur absolue du produit d'un nombre fini de nombres réels est égale au produit des valeurs absolues des facteurs : │а·в│=│а│·│в│ Propriété n°5 : La valeur absolue du quotient des nombres réels est égale au quotient de leurs valeurs absolues :

Section 3. Interprétation géométrique de la notion de module d'un nombre.

Chaque nombre réel peut être associé à un point sur la droite numérique, qui sera une image géométrique de ce nombre réel. Chaque point de la droite numérique correspond à sa distance par rapport à l'origine, c'est-à-dire la longueur du segment depuis l'origine jusqu'à un point donné. Cette distance est toujours considérée comme une valeur non négative. Par conséquent, la longueur du segment correspondant sera l’interprétation géométrique de la valeur absolue d’un nombre réel donné.

L'illustration géométrique présentée confirme clairement la propriété n°1, c'est-à-dire les modules des nombres opposés sont égaux. De là, la validité de l'égalité est facilement comprise : │х – а│= │а – x│. La solution de l'équation │x│= m, où m ≥ 0, à savoir x 1,2 = ± m, devient également plus évidente. Exemples: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2 ; 4

Section 4. Graphique de la fonction y = │х│

Le domaine de cette fonction est constitué de tous les nombres réels.

Section 5. Conventions.

À l'avenir, lors de l'examen d'exemples de résolution d'équations, les conventions suivantes seront utilisées : ( - signe du système [ - signe de la totalité Lors de la résolution d'un système d'équations (inégalités), l'intersection des solutions des équations (inégalités) incluses dans le système est trouvée. Lors de la résolution d'un ensemble d'équations (inégalités), l'union des solutions incluses dans l'ensemble d'équations (inégalités) est trouvée.

Chapitre 2. Résolution d'équations contenant un module.

Dans ce chapitre, nous examinerons les méthodes algébriques pour résoudre des équations contenant un ou plusieurs modules.

Section 1. Équations de la forme │F (x)│= m

Une équation de ce type est dite la plus simple. Elle a une solution si et seulement si m ≥ 0. Par définition du module, l'équation originale est équivalente à un ensemble de deux équations : │ F(x)│=m
Exemples:
№1. Résolvez l'équation : │7х - 2│= 9


Réponse : x 1 = - 1 ; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1 ; x 2 = -2 x (x + 3) = 0 x 1 = 0 ; x2 = -3 Réponse : la somme des racines est - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 désigne x 2 = m, m ≥ 0 x = 0 ; ±√5 m2 – 5 m + 4 = 0 m = 1 ; 4 – les deux valeurs satisfont à la condition m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Réponse : nombre de racines de l'équation 7. Des exercices:
№1. Résolvez l'équation et indiquez la somme des racines : │х - 5│= 3 №2 . Résolvez l'équation et indiquez la racine la plus petite : │x 2 + x│= 0 №3 . Résolvez l'équation et indiquez la plus grande racine : │x 2 – 5x + 4│= 4 №4 .Résolvez l'équation et indiquez la racine entière : │2x 2 – 7x + 6│= 1 №5 .Résolvez l'équation et indiquez le nombre de racines : │x 4 – 13x 2 + 50│= 14

Section 2. Équations de la forme F(│х│) = m

L'argument de la fonction sur le côté gauche est sous le signe du module et le côté droit est indépendant de la variable. Considérons deux manières de résoudre des équations de ce type. 1 manière : Par définition de valeur absolue, l'équation originale équivaut à la combinaison de deux systèmes. Dans chacun d'entre eux, une condition est imposée à une expression sous-modulaire. F(│х│) =m
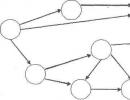
Puisque la fonction F(│x│) est paire dans tout le domaine de définition, les racines des équations F(x) = m et F(- x) = m sont des paires de nombres opposés. Par conséquent, il suffit de résoudre l'un des systèmes (en considérant des exemples de cette manière, la solution d'un système sera donnée). Méthode 2 : Application de la méthode d'introduction d'une nouvelle variable. Dans ce cas, la désignation │x│= a est introduite, où a ≥ 0. Cette méthode est de conception moins volumineuse.
Exemples: №1 . Résolvez l’équation : 3x 2 – 4│x│= - 1 Utilisons l’introduction d’une nouvelle variable. Notons │x│= a, où a ≥ 0. On obtient l'équation 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Retour à la variable d'origine : │ x│=1 et │х│= 1/3. Chaque équation a deux racines. Réponse : x 1 = 1 ; X 2 = - 1 ; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Résolvez l'équation : 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
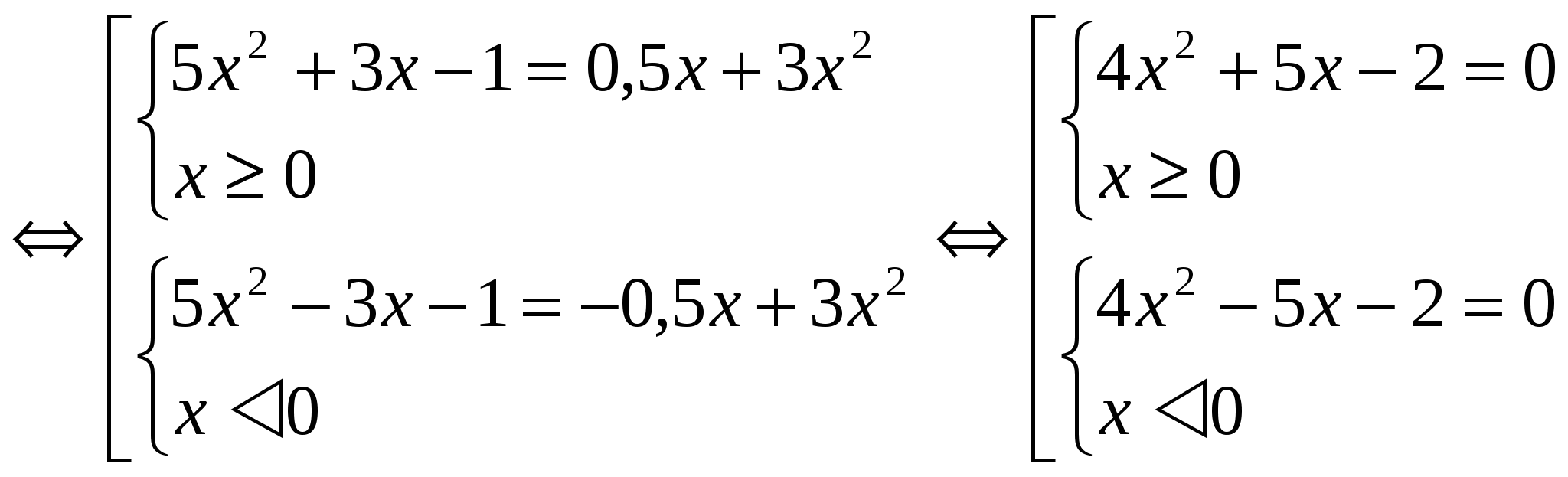Trouvons la solution du premier système de la population : 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Notez que x 2 ne satisfait pas la condition x ≥ 0. Solution le deuxième système sera le nombre opposé à la valeur x 1. Réponse : x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Résolvez l'équation : x 4 – │х│= 0 Notons │х│= a, où a ≥ 0. On obtient l'équation a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Retour à la variable d'origine : │х│=0 et │х│= 1 x = 0 ; ± 1 Réponse : x 1 = 0 ; X 2 = 1 ; X 3 = - 1.
Des exercices: №6. Résolvez l'équation : 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Résolvez l'équation, indiquez le nombre de racines dans votre réponse : 3x 2 - 7│x│ + 2 = 0 №8 . Résolvez l'équation, indiquez les solutions entières dans votre réponse : x 4 + │x│ - 2 = 0

Section 3. Équations de la forme │F(x)│ = G(x)

Le membre de droite d’une équation de ce type dépend d’une variable et a donc une solution si et seulement si le membre de droite est une fonction G(x) ≥ 0. L’équation originale peut être résolue de deux manières : 1 manière : Standard, basé sur la divulgation d'un module basé sur sa définition et consiste en une transition équivalente vers une combinaison de deux systèmes. │ F(x)│ =g(X)

Cette méthode peut être utilisée rationnellement dans le cas d’une expression complexe pour la fonction G(x) et moins complexe pour la fonction F(x), puisqu’on suppose que les inégalités avec la fonction F(x) seront résolues. Méthode 2 : Consiste en le passage à un système équivalent dans lequel une condition est imposée au côté droit. │ F(X)│= g(X)

Cette méthode est plus pratique à utiliser si l'expression de la fonction G(x) est moins complexe que celle de la fonction F(x), puisque la solution de l'inégalité G(x) ≥ 0 est supposée de plus, dans le cas. de plusieurs modules, il est recommandé d'utiliser la deuxième option. Exemples: №1. Résolvez l'équation : │x + 2│= 6 -2x
(1 voie) Réponse : x = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(x + 1)
(2 voies) Réponse : Le produit des racines est 3.
№3. Résolvez l'équation et indiquez la somme des racines dans votre réponse :
│x - 6│= x 2 - 5x + 9

Réponse : la somme des racines est 4.
Des exercices: №9. │x + 4│= - 3x №10. Résolvez l'équation, indiquez le nombre de solutions dans votre réponse :│x 2 + x - 1│= 2x – 1 №11 . Résolvez l'équation, indiquez le produit des racines dans votre réponse :│x + 3│= x 2 + x – 6

Section 4. Équations de la forme │F(x)│= F(x) et │F(x)│= - F(x)

Les équations de ce type sont parfois appelées « les plus belles ». Puisque le membre de droite des équations dépend de la variable, des solutions existent si et seulement si le membre de droite est non négatif. Par conséquent, les équations originales sont équivalentes aux inégalités :
│F(x)│= F(x) F(x) ≥ 0 et │F(x)│= - F(x) F(x) Exemples: №1 . Résolvez l'équation, indiquez la racine entière la plus petite dans votre réponse : │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Réponse : x = 1№2. Résolvez l'équation, indiquez la longueur de l'intervalle dans votre réponse : │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3 ; 3] Réponse : la longueur de l’écart est de 6.№3 . Résolvez l'équation et indiquez le nombre de solutions entières dans votre réponse : │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1 ; 2] Réponse : 4 solutions entières.№4 . Résolvez l’équation et indiquez la plus grande racine dans votre réponse :
│4 – x-
│= 4 – x –
x 2 – 5x + 5 = 0 D = 5 x 1,2 =
≈ 1,4

Réponse : x = 3.

Des exercices: №12. Résolvez l'équation, indiquez la racine entière dans la réponse : │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Résolvez l'équation, indiquez le nombre de solutions entières dans votre réponse : │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Résolvez l'équation ; dans votre réponse, indiquez un entier qui n'est pas la racine de l'équation :

Section 5. Équations de la forme │F(x)│= │G(x)│

Puisque les deux côtés de l’équation sont non négatifs, la solution implique de considérer deux cas : les expressions sous-modulaires sont de signe égal ou opposé. L’équation originale est donc équivalente à la combinaison de deux équations : │ F(X)│= │ g(X)│
Exemples: №1. Résolvez l'équation, indiquez la racine entière dans votre réponse : │x + 3│=│2x - 1│
Réponse : racine entière x = 4.№2. Résous l'équation: │ x – x 2 - 1│=│2x – 3 – x 2 │
Réponse : x = 2.№3 . Résolvez l'équation et indiquez le produit des racines dans votre réponse :




Équations racine 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Réponse : le produit des racines est de – 0,25. Des exercices: №15 . Résolvez l'équation et indiquez la solution complète dans votre réponse : │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Résolvez l'équation, indiquez la racine la plus petite dans votre réponse :│5x - 3│=│7 - x│ №17 . Résolvez l'équation et indiquez la somme des racines dans votre réponse :

Section 6. Exemples de résolution d'équations non standard

Dans cette section, nous examinerons des exemples d'équations non standard, lors de la résolution desquelles la valeur absolue de l'expression est révélée par définition. Exemples:

№1. Résolvez l'équation, indiquez la somme des racines dans votre réponse : x · │x│- 5x – 6 = 0
Réponse : la somme des racines est 1 №2. . Résolvez l'équation, indiquez la racine la plus petite dans votre réponse : x 2 - 4x ·
- 5 = 0
Réponse : racine plus petite x = - 5. №3. Résous l'équation:

Réponse : x = -1. Des exercices: №18. Résolvez l'équation et indiquez la somme des racines : x · │3x + 5│= 3x 2 + 4x + 3
№19. Résolvez l'équation : x 2 – 3x =

№20. Résous l'équation:

Section 7. Équations de la forme │F(x)│+│G(x)│=0

Il est facile de remarquer que sur le côté gauche de l’équation de ce type se trouve la somme des quantités non négatives. Par conséquent, l’équation originale a une solution si et seulement si les deux termes sont égaux à zéro en même temps. L'équation est équivalente au système d'équations : │ F(X)│+│ g(X)│=0
Exemples: №1 . Résous l'équation:
Réponse : x = 2. №2. Résous l'équation: Réponse : x = 1. Des exercices: №21. Résous l'équation: №22 . Résolvez l'équation et indiquez la somme des racines dans votre réponse : №23 . Résolvez l'équation et indiquez le nombre de solutions dans votre réponse :

Section 8. Équations de la forme │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

Pour résoudre des équations de ce type, la méthode des intervalles est utilisée. Si nous le résolvons par expansion séquentielle des modules, nous obtenons n ensembles de systèmes, ce qui est très lourd et peu pratique. Considérons l'algorithme de la méthode des intervalles : 1). Rechercher des valeurs de variables X, pour lequel chaque module est égal à zéro (zéros des expressions sous-modulaires) :
2). Marquez les valeurs trouvées sur une droite numérique divisée en intervalles (le nombre d'intervalles est respectivement égal à n+1 ) 3). Déterminez avec quel signe chaque module est révélé à chacun des intervalles obtenus (lors de l'élaboration d'une solution, vous pouvez utiliser une droite numérique en marquant les signes dessus) 4). L'équation originale est équivalente à l'agrégat n+1 systèmes, dans chacun desquels l’appartenance de la variable est indiquée X l'un des intervalles. Exemples: №1 . Résolvez l’équation et indiquez la plus grande racine dans votre réponse :
1). Trouvons les zéros des expressions sous-modulaires : x = 2 ; x = -3 2). Marquons les valeurs trouvées sur la droite numérique et déterminons avec quel signe chaque module est révélé sur les intervalles résultants :
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- pas de solutions L'équation a deux racines. Réponse : la plus grande racine x = 2. №2. Résolvez l’équation et fournissez la racine entière dans votre réponse :
1). Trouvons les zéros des expressions sous-modulaires : x = 1,5 ; x = - 1 2). Marquons les valeurs trouvées sur la droite numérique et déterminons avec quel signe chaque module est révélé sur les intervalles résultants : x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
Le dernier système n’a pas de solution, donc l’équation a deux racines. Lors de la résolution de l'équation, vous devez faire attention au signe « - » devant le deuxième module. Réponse : racine entière x = 7. №3. Résolvez l'équation, indiquez la somme des racines dans votre réponse : 1). Trouvons les zéros des expressions sous-modulaires : x = 5 ; x = 1 ; x = - 2 2). Marquons les valeurs trouvées sur la droite numérique et déterminons avec quel signe chaque module est révélé aux intervalles résultants : x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
L'équation a deux racines x = 0 et 2. Réponse : la somme des racines est 2. №4 . Résolvez l'équation : 1). Trouvons les zéros des expressions sous-modulaires : x = 1 ; x = 2 ; x = 3.2). Déterminons avec quel signe chaque module se révèle sur les intervalles résultants. 3).
Combinons les solutions des trois premiers systèmes. Répondre: ; x = 5.
Des exercices: №24. Résous l'équation:
№25. Résolvez l’équation et indiquez la somme des racines dans votre réponse : №26. Résolvez l’équation et indiquez la racine la plus petite dans votre réponse : №27. Résolvez l’équation et indiquez la plus grande racine dans votre réponse :

Section 9. Équations contenant plusieurs modules

Les équations contenant plusieurs modules supposent la présence de valeurs absolues dans les expressions sous-modulaires. Le principe de base pour résoudre des équations de ce type est la divulgation séquentielle des modules, en commençant par celui « externe ». Lors de la résolution, les techniques abordées dans les sections n° 1, n° 3 sont utilisées.

Exemples: №1. Résous l'équation:
Réponse : x = 1 ; - onze. №2. Résous l'équation:
Réponse : x = 0 ; 4 ; - 4. №3. Résolvez l'équation et indiquez le produit des racines dans votre réponse :
Réponse : le produit des racines est – 8. №4. Résous l'équation:
Notons les équations de la population (1) Et (2) et considérez la solution pour chacun d’eux séparément pour faciliter la conception. Étant donné que les deux équations contiennent plus d’un module, il est plus pratique d’effectuer une transition équivalente vers des ensembles de systèmes. (1)

(2)


Répondre:
Des exercices: №36. Résolvez l'équation, indiquez la somme des racines dans votre réponse : 5 │3x-5│ = 25 x №37. Résolvez l'équation, s'il y a plus d'une racine, indiquez la somme des racines dans votre réponse : │x + 2│ x – 3x – 10 = 1 №38. Résolvez l'équation : 3 │2х -4│ = 9 │х│ №39. Résolvez l'équation, dans votre réponse indiquez le nombre de racines par : 2 │ sin x│ = √2 №40 . Résolvez l'équation et indiquez le nombre de racines dans votre réponse :

Section 3. Équations logarithmiques.

Avant de résoudre les équations suivantes, il est nécessaire de revoir les propriétés des logarithmes et de la fonction logarithmique. Exemples: №1. Résolvez l'équation, indiquez le produit des racines dans votre réponse : log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Cas 1 : si x ≥ - 1, alors log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – satisfait la condition x ≥ - 1 2 cas : si x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – satisfait à la condition x - 1
Réponse : le produit des racines est – 15.
№2. Résolvez l'équation, indiquez la somme des racines dans votre réponse : lg
O.D.Z.

Réponse : la somme des racines est de 0,5.
№3. Résoudre l'équation : log 5
O.D.Z.

Réponse : x = 9. №4. Résolvez l'équation : │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Utilisons la formule pour passer à une autre base. │2 - journal 5 x│+ 3 = │1 + journal 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Trouvons les zéros des expressions sous-modulaires : x = 25 ; x = Ces nombres divisent la plage de valeurs acceptables en trois intervalles, l'équation équivaut donc à un ensemble de trois systèmes.
Répondre: )