ការដោះស្រាយសមីការ និងវិសមភាពជាមួយម៉ូឌុលជារឿយៗបណ្តាលឱ្យមានការលំបាក។ ទោះយ៉ាងណាក៏ដោយប្រសិនបើអ្នកយល់ច្បាស់ថាវាជាអ្វី តម្លៃដាច់ខាតនៃលេខមួយ។, និង របៀបពង្រីកកន្សោមដែលមានសញ្ញាម៉ូឌុលឱ្យបានត្រឹមត្រូវបន្ទាប់មកវត្តមាននៅក្នុងសមីការ កន្សោមនៅក្រោមសញ្ញាម៉ូឌុលឈប់ជាឧបសគ្គចំពោះដំណោះស្រាយរបស់វា។

ទ្រឹស្តីតិចតួច។ លេខនីមួយៗមានលក្ខណៈពីរ៖ តម្លៃដាច់ខាតនៃលេខ និងសញ្ញារបស់វា។

ឧទាហរណ៍ លេខ +5 ឬសាមញ្ញ 5 មានសញ្ញា "+" និងតម្លៃដាច់ខាតនៃ 5 ។

លេខ -5 មានសញ្ញា "-" និងតម្លៃដាច់ខាតនៃ 5 ។

តម្លៃដាច់ខាតនៃលេខ 5 និង -5 គឺ 5 ។

តម្លៃដាច់ខាតនៃចំនួន x ត្រូវបានគេហៅថាម៉ូឌុលនៃលេខ ហើយត្រូវបានតាងដោយ |x|។

ដូចដែលយើងឃើញ ម៉ូឌុលនៃលេខគឺស្មើនឹងលេខខ្លួនវា ប្រសិនបើលេខនេះធំជាង ឬស្មើសូន្យ ហើយចំពោះលេខនេះដែលមានសញ្ញាផ្ទុយ ប្រសិនបើលេខនេះគឺអវិជ្ជមាន។

ដូចគ្នានេះដែរអនុវត្តចំពោះកន្សោមណាមួយដែលលេចឡើងនៅក្រោមសញ្ញាម៉ូឌុល។

ច្បាប់ពង្រីកម៉ូឌុលមើលទៅដូចនេះ៖

|f(x)|= f(x) ប្រសិនបើ f(x) ≥ 0, និង

|f(x)|= - f(x) ប្រសិនបើ f(x)< 0

ឧទាហរណ៍ |x-3|=x-3 ប្រសិនបើ x-3≥0 និង |x-3|=-(x-3)=3-x ប្រសិនបើ x-3<0.

ដើម្បីដោះស្រាយសមីការដែលមានកន្សោមនៅក្រោមសញ្ញាម៉ូឌុល អ្នកត្រូវតែដំបូង ពង្រីកម៉ូឌុលមួយយោងទៅតាមច្បាប់ពង្រីកម៉ូឌុល.

បន្ទាប់មកសមីការ ឬវិសមភាពរបស់យើងក្លាយជា ទៅជាសមីការពីរផ្សេងគ្នាដែលមាននៅលើចន្លោះលេខពីរផ្សេងគ្នា។

សមីការមួយមាននៅលើចន្លោះលេខដែលកន្សោមនៅក្រោមសញ្ញាម៉ូឌុលគឺមិនអវិជ្ជមាន។

ហើយសមីការទីពីរមាននៅលើចន្លោះពេលដែលកន្សោមនៅក្រោមសញ្ញាម៉ូឌុលគឺអវិជ្ជមាន។

សូមក្រឡេកមើលឧទាហរណ៍ដ៏សាមញ្ញមួយ។

តោះដោះស្រាយសមីការ៖

|x-3|=-x 2 +4x-3

1. តោះបើកម៉ូឌុល។

|x-3|=x-3 ប្រសិនបើ x-3≥0, i.e. ប្រសិនបើ x≥3

|x-3|=-(x-3)=3-x ប្រសិនបើ x-3<0, т.е. если х<3

2. យើងបានទទួលចន្លោះលេខពីរ៖ x≥3 និង x<3.

ចូរយើងពិចារណាថាតើសមីការណាដែលសមីការដើមត្រូវបានបំប្លែងលើចន្លោះនីមួយៗ៖

ក) សម្រាប់ x≥3 |x-3|=x-3 ហើយការរបួសរបស់យើងមានទម្រង់៖

យកចិត្តទុកដាក់! សមីការនេះមាននៅលើចន្លោះពេល x≥3 ប៉ុណ្ណោះ!

តោះបើកតង្កៀប ហើយបង្ហាញពាក្យស្រដៀងគ្នានេះ៖

និងដោះស្រាយសមីការនេះ។

សមីការនេះមានឫសគល់៖

x 1 = 0, x 2 = 3

យកចិត្តទុកដាក់! ដោយសារសមីការ x-3=-x 2 +4x-3 មាននៅលើចន្លោះពេល x≥3 យើងចាប់អារម្មណ៍តែលើឫសទាំងនោះដែលជាកម្មសិទ្ធិរបស់ចន្លោះពេលនេះ។ លក្ខខណ្ឌនេះត្រូវបានពេញចិត្តដោយ x 2 = 3 ប៉ុណ្ណោះ។

ខ) នៅ x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

យកចិត្តទុកដាក់! សមីការនេះមាននៅលើចន្លោះ x ប៉ុណ្ណោះ។<3!

តោះបើកតង្កៀប ហើយបង្ហាញពាក្យស្រដៀងគ្នា។ យើងទទួលបានសមីការ៖

x 1 = 2, x 2 = 3

យកចិត្តទុកដាក់! ដោយសារសមីការ 3-x=-x 2 +4x-3 មាននៅលើចន្លោះ x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

ដូច្នេះ៖ ចាប់ពីចន្លោះពេលដំបូង យើងយកតែ root x=3 ពីទីពីរ - root x=2។

ម៉ូឌុលគឺជាតម្លៃដាច់ខាតនៃកន្សោម។ ដើម្បីបង្ហាញម៉ូឌុលណាមួយ វាជាទម្លាប់ក្នុងការប្រើតង្កៀបត្រង់។ តម្លៃដែលត្រូវបានរុំព័ទ្ធក្នុងតង្កៀបគូគឺជាតម្លៃដែលត្រូវបានយកម៉ូឌុល។ ដំណើរការនៃការដោះស្រាយម៉ូឌុលណាមួយរួមមានការបើកតង្កៀបត្រង់ទាំងនោះ ដែលនៅក្នុងភាសាគណិតវិទ្យាត្រូវបានគេហៅថាតង្កៀបម៉ូឌុល។ ការបង្ហាញរបស់ពួកគេកើតឡើងយោងទៅតាមច្បាប់មួយចំនួន។ ដូចគ្នានេះផងដែរនៅក្នុងលំដាប់នៃការដោះស្រាយម៉ូឌុល សំណុំនៃតម្លៃនៃកន្សោមទាំងនោះដែលមាននៅក្នុងតង្កៀបម៉ូឌុលត្រូវបានរកឃើញ។ ក្នុងករណីភាគច្រើន ម៉ូឌុលត្រូវបានពង្រីកតាមរបៀបដែលកន្សោមដែលមានលក្ខណៈ submodular ទទួលបានទាំងតម្លៃវិជ្ជមាន និងអវិជ្ជមាន រួមទាំងតម្លៃសូន្យ។ ប្រសិនបើយើងចាប់ផ្តើមពីលក្ខណៈសម្បត្តិដែលបានបង្កើតឡើងនៃម៉ូឌុល នោះនៅក្នុងដំណើរការសមីការ ឬវិសមភាពផ្សេងៗពីកន្សោមដើមត្រូវបានចងក្រង ដែលបន្ទាប់មកចាំបាច់ត្រូវដោះស្រាយ។ ចូរយើងស្វែងយល់ពីរបៀបដោះស្រាយម៉ូឌុល។

ដំណើរការដំណោះស្រាយ

ការដោះស្រាយម៉ូឌុលចាប់ផ្តើមដោយការសរសេរសមីការដើមជាមួយម៉ូឌុល។ ដើម្បីឆ្លើយសំណួរអំពីរបៀបដោះស្រាយសមីការជាមួយម៉ូឌុល អ្នកត្រូវបើកវាទាំងស្រុង។ ដើម្បីដោះស្រាយសមីការបែបនេះ ម៉ូឌុលត្រូវបានពង្រីក។ កន្សោមម៉ូឌុលទាំងអស់ត្រូវតែយកមកពិចារណា។ វាចាំបាច់ក្នុងការកំណត់តម្លៃនៃបរិមាណដែលមិនស្គាល់រួមបញ្ចូលនៅក្នុងសមាសភាពរបស់វាកន្សោមម៉ូឌុលនៅក្នុងតង្កៀបក្លាយជាសូន្យ។ ដើម្បីធ្វើដូច្នេះបាន វាគ្រប់គ្រាន់ហើយក្នុងការសមីការកន្សោមនៅក្នុងតង្កៀបម៉ូឌុលទៅសូន្យ ហើយបន្ទាប់មកគណនាដំណោះស្រាយទៅនឹងសមីការលទ្ធផល។ តម្លៃដែលបានរកឃើញត្រូវតែកត់ត្រា។ ដូចគ្នាដែរ អ្នកក៏ត្រូវកំណត់តម្លៃនៃអថេរដែលមិនស្គាល់ទាំងអស់សម្រាប់ម៉ូឌុលទាំងអស់នៅក្នុងសមីការនេះ។ បន្ទាប់មកទៀត វាចាំបាច់ក្នុងការកំណត់ និងពិចារណាករណីទាំងអស់នៃអត្ថិភាពនៃអថេរនៅក្នុងកន្សោម នៅពេលដែលវាខុសពីតម្លៃសូន្យ។ ដើម្បីធ្វើដូចនេះអ្នកត្រូវសរសេរប្រព័ន្ធមួយចំនួននៃវិសមភាពដែលត្រូវគ្នានឹងម៉ូឌុលទាំងអស់នៅក្នុងវិសមភាពដើម។ វិសមភាពត្រូវតែសរសេរដើម្បីឱ្យវាគ្របដណ្តប់តម្លៃដែលមាន និងអាចធ្វើទៅបានទាំងអស់សម្រាប់អថេរដែលត្រូវបានរកឃើញនៅលើបន្ទាត់លេខ។ បន្ទាប់មកអ្នកត្រូវគូរបន្ទាត់លេខដូចគ្នានេះសម្រាប់ការមើលឃើញ ដែលនៅពេលក្រោយនឹងគូរតម្លៃដែលទទួលបានទាំងអស់។

ឥឡូវនេះ អ្វីៗស្ទើរតែទាំងអស់អាចធ្វើបាននៅលើអ៊ីនធឺណិត។ ម៉ូឌុលមិនមានករណីលើកលែងចំពោះច្បាប់ទេ។ អ្នកអាចដោះស្រាយវាតាមអ៊ីនធឺណិតលើធនធានទំនើបមួយក្នុងចំណោមធនធានទំនើបៗជាច្រើន។ តម្លៃទាំងអស់នៃអថេរដែលមាននៅក្នុងម៉ូឌុលសូន្យនឹងជាឧបសគ្គពិសេសដែលនឹងត្រូវបានប្រើនៅក្នុងដំណើរការនៃការដោះស្រាយសមីការម៉ូឌុល។ នៅក្នុងសមីការដើម អ្នកត្រូវបើកតង្កៀបម៉ូឌុលដែលមានទាំងអស់ ខណៈពេលដែលផ្លាស់ប្តូរសញ្ញានៃកន្សោម ដូច្នេះតម្លៃនៃអថេរដែលចង់បានស្របគ្នាជាមួយនឹងតម្លៃទាំងនោះដែលអាចមើលឃើញនៅលើបន្ទាត់លេខ។ សមីការលទ្ធផលត្រូវតែដោះស្រាយ។ តម្លៃនៃអថេរដែលនឹងទទួលបានកំឡុងពេលដោះស្រាយសមីការត្រូវតែពិនិត្យប្រឆាំងនឹងដែនកំណត់ដែលបានបញ្ជាក់ដោយម៉ូឌុលខ្លួនឯង។ ប្រសិនបើតម្លៃនៃអថេរបំពេញលក្ខខណ្ឌយ៉ាងពេញលេញ នោះវាត្រឹមត្រូវ។ ឫសទាំងអស់ដែលនឹងទទួលបានក្នុងអំឡុងពេលដំណោះស្រាយនៃសមីការ ប៉ុន្តែនឹងមិនសមនឹងការរឹតបន្តឹងទេ ត្រូវតែបោះបង់ចោល។

អនុវិទ្យាល័យ MBOU លេខ 17 អ៊ីវ៉ាណូវ៉ូ

« សមីការជាមួយម៉ូឌុល"
ការអភិវឌ្ឍន៍វិធីសាស្រ្ត

ចងក្រង

គ្រូគណិតវិទ្យា

Lebedeva N.V.

ឆ្នាំ 20010

កំណត់ចំណាំពន្យល់

ជំពូកទី 1. សេចក្តីផ្តើម

ផ្នែកទី 2. លក្ខណៈសម្បត្តិមូលដ្ឋាន ផ្នែកទី 3. ការបកស្រាយធរណីមាត្រនៃគំនិតនៃម៉ូឌុលនៃចំនួនមួយ។ ផ្នែកទី 4. ក្រាហ្វនៃអនុគមន៍ y = |x| ផ្នែកទី 5. អនុសញ្ញា

ជំពូកទី 2. ការដោះស្រាយសមីការដែលមានម៉ូឌុល

ផ្នែកទី 1. សមីការនៃទម្រង់ |F(x)| = m (សាមញ្ញបំផុត) ផ្នែកទី 2. សមីការនៃទម្រង់ F(|x|) = m ផ្នែកទី 3. សមីការនៃទម្រង់ |F(x)| = G(x) ផ្នែកទី 4. សមីការនៃទម្រង់ |F(x)| = ± F(x) (ស្អាតបំផុត) ផ្នែកទី 5. សមីការនៃទម្រង់ |F(x)| = |G(x)| ផ្នែកទី 6. ឧទាហរណ៍នៃការដោះស្រាយសមីការមិនស្តង់ដារ ផ្នែកទី 7. សមីការនៃទម្រង់ |F(x)| + |G(x)| = 0 ផ្នែកទី 8. សមីការនៃទម្រង់ |a 1 x ± b 1 | ± |a 2 x ± b 2 | ± …|a n x ± ក្នុង n| = ម ផ្នែកទី 9. សមីការដែលមានម៉ូឌុលជាច្រើន។

ជំពូកទី 3. ឧទាហរណ៍នៃការដោះស្រាយសមីការផ្សេងៗជាមួយម៉ូឌុល។

ផ្នែកទី 1. សមីការត្រីកោណមាត្រ ផ្នែកទី 2. សមីការអិចស្ប៉ូណង់ស្យែល ផ្នែកទី 3. សមីការលោការីត ផ្នែកទី 4. សមីការមិនសមហេតុផល ផ្នែកទី 5. កិច្ចការកម្រិតខ្ពស់ ចម្លើយចំពោះលំហាត់ គន្ថនិទ្ទេស

កំណត់ចំណាំពន្យល់។

គោលគំនិតនៃតម្លៃដាច់ខាត (ម៉ូឌុល) នៃចំនួនពិត គឺជាលក្ខណៈសំខាន់មួយរបស់វា។ គំនិតនេះត្រូវបានរីករាលដាលនៅក្នុងផ្នែកផ្សេងៗនៃវិទ្យាសាស្ត្ររូបវិទ្យា គណិតវិទ្យា និងបច្ចេកទេស។ នៅក្នុងការអនុវត្តនៃការបង្រៀនមុខវិជ្ជាគណិតវិទ្យានៅអនុវិទ្យាល័យស្របតាមកម្មវិធីរបស់ក្រសួងការពារជាតិនៃសហព័ន្ធរុស្ស៊ីគំនិតនៃ "តម្លៃដាច់ខាតនៃលេខ" ត្រូវបានជួបប្រទះម្តងហើយម្តងទៀត: នៅថ្នាក់ទី 6 និយមន័យនៃម៉ូឌុលនិង អត្ថន័យធរណីមាត្ររបស់វាត្រូវបានណែនាំ; នៅថ្នាក់ទី 8 គំនិតនៃកំហុសដាច់ខាតត្រូវបានបង្កើតឡើងដំណោះស្រាយនៃសមីការសាមញ្ញបំផុតនិងវិសមភាពដែលមានម៉ូឌុលត្រូវបានពិចារណាហើយលក្ខណៈសម្បត្តិនៃឫសការ៉េនព្វន្ធត្រូវបានសិក្សា។ នៅថ្នាក់ទី 11 គំនិតត្រូវបានរកឃើញនៅក្នុងផ្នែក "ឫស ន- សញ្ញាបត្រ” ។បទពិសោធន៍នៃការបង្រៀនបង្ហាញថា សិស្សតែងតែជួបប្រទះការលំបាកក្នុងការដោះស្រាយកិច្ចការដែលទាមទារចំណេះដឹងអំពីសម្ភារៈនេះ ហើយជារឿយៗរំលងវាដោយមិនចាប់ផ្តើមបញ្ចប់វា។ អត្ថបទនៃកិច្ចការប្រឡងសម្រាប់វគ្គសិក្សាថ្នាក់ទី ៩ និងទី ១១ ក៏រួមបញ្ចូលកិច្ចការស្រដៀងគ្នាដែរ។ លើសពីនេះតម្រូវការដែលសាកលវិទ្យាល័យដាក់លើនិស្សិតបញ្ចប់ការសិក្សាគឺខុសគ្នា ពោលគឺនៅកម្រិតខ្ពស់ជាងតម្រូវការនៃកម្មវិធីសិក្សារបស់សាលា។ សម្រាប់ជីវិតនៅក្នុងសង្គមសម័យទំនើប ការបង្កើតរចនាប័ទ្មនៃការគិតបែបគណិតវិទ្យា ដែលបង្ហាញឱ្យឃើញពីជំនាញផ្លូវចិត្តជាក់លាក់ គឺមានសារៈសំខាន់ខ្លាំងណាស់។ នៅក្នុងដំណើរការនៃការដោះស្រាយបញ្ហាជាមួយម៉ូឌុល សមត្ថភាពក្នុងការប្រើប្រាស់បច្ចេកទេសដូចជា ទូទៅ និងការបញ្ជាក់ ការវិភាគ ចំណាត់ថ្នាក់ និងការរៀបចំប្រព័ន្ធ និងភាពស្រដៀងគ្នាត្រូវបានទាមទារ។ ការដោះស្រាយកិច្ចការបែបនេះអនុញ្ញាតឱ្យអ្នកសាកល្បងចំណេះដឹងរបស់អ្នកអំពីផ្នែកសំខាន់ៗនៃវគ្គសិក្សារបស់សាលា កម្រិតនៃការគិតឡូជីខល និងជំនាញស្រាវជ្រាវដំបូង។ ការងារនេះត្រូវបានឧទ្ទិសដល់ផ្នែកមួយ - ការដោះស្រាយសមីការដែលមានម៉ូឌុល។ វាមានបីជំពូក។ ជំពូកទីមួយណែនាំអំពីគោលគំនិតជាមូលដ្ឋាន និងការពិចារណាទ្រឹស្តីសំខាន់ៗបំផុត។ ជំពូកទី 2 ស្នើសមីការសំខាន់ៗចំនួនប្រាំបួនដែលមានម៉ូឌុល ពិភាក្សាអំពីវិធីសាស្រ្តសម្រាប់ដោះស្រាយពួកវា និងពិនិត្យមើលឧទាហរណ៍នៃកម្រិតផ្សេងគ្នានៃភាពស្មុគស្មាញ។ ជំពូកទីបីផ្តល់នូវសមីការស្មុគស្មាញ និងមិនមានស្តង់ដារ (ត្រីកោណមាត្រ អិចស្ប៉ូណង់ស្យែល លោការីត និងអសមហេតុផល)។ សម្រាប់ប្រភេទសមីការនីមួយៗមានលំហាត់សម្រាប់ដោះស្រាយដោយឯករាជ្យ (ចម្លើយ និងការណែនាំត្រូវបានភ្ជាប់)។ គោលបំណងសំខាន់នៃការងារនេះគឺផ្តល់ជំនួយផ្នែកវិធីសាស្រ្តដល់គ្រូបង្រៀនក្នុងការរៀបចំមេរៀន និងក្នុងការរៀបចំវគ្គសិក្សាជ្រើសរើស។ សម្ភារៈក៏អាចប្រើជាជំនួយការបង្រៀនសម្រាប់សិស្សវិទ្យាល័យផងដែរ។ កិច្ចការដែលបានស្នើឡើងក្នុងការងារគឺគួរឱ្យចាប់អារម្មណ៍ ហើយមិនតែងតែងាយស្រួលក្នុងការដោះស្រាយនោះទេ ដែលធ្វើឱ្យវាអាចធ្វើឱ្យការលើកទឹកចិត្តផ្នែកអប់រំរបស់សិស្សកាន់តែមានស្មារតី សាកល្បងសមត្ថភាពរបស់ពួកគេ និងបង្កើនកម្រិតនៃការរៀបចំនិស្សិតបញ្ចប់ការសិក្សាសម្រាប់ចូលសាកលវិទ្យាល័យ។ ការជ្រើសរើសភាពខុសគ្នានៃលំហាត់ដែលបានស្នើឡើងពាក់ព័ន្ធនឹងការផ្លាស់ប្តូរពីកម្រិតបន្តពូជនៃការធ្វើជាម្ចាស់លើសម្ភារៈទៅជាការច្នៃប្រឌិត ក៏ដូចជាឱកាសដើម្បីបង្រៀនពីរបៀបអនុវត្តចំណេះដឹងរបស់អ្នកនៅពេលដោះស្រាយបញ្ហាដែលមិនមានស្តង់ដារ។

ជំពូកទី 1. សេចក្តីផ្តើម។

ផ្នែកទី 1. ការកំណត់តម្លៃដាច់ខាត .

និយមន័យ : តម្លៃដាច់ខាត (ម៉ូឌុល) នៃចំនួនពិត កលេខដែលមិនអវិជ្ជមានត្រូវបានគេហៅថា៖ កឬ - ក. ការកំណត់: │ ក │ ធាតុអានដូចខាងក្រោមៈ "ម៉ូឌុលនៃលេខ a" ឬ "តម្លៃដាច់ខាតនៃលេខ a"

│ a ប្រសិនបើ a > 0

│a│ = │ 0 ប្រសិនបើ a = 0 (1)

│ - ហើយប្រសិនបើ ក
ឧទាហរណ៍: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

ពង្រីកម៉ូឌុលកន្សោម៖

ក) │x − 8│ ប្រសិនបើ x > 12 ខ) │2x + 3│ ប្រសិនបើ x ≤ −2 │x – 8│= x – 8 │ 2x + 3│= − 2x – 3

ផ្នែកទី 2. លក្ខណៈសម្បត្តិមូលដ្ឋាន។

ចូរយើងពិចារណាអំពីលក្ខណៈសម្បត្តិជាមូលដ្ឋាននៃតម្លៃដាច់ខាត។ អចលនទ្រព្យលេខ ១៖ លេខទល់មុខមានម៉ូឌុលស្មើគ្នា i.e. │а│=│- а│ចូរយើងបង្ហាញថាសមភាពគឺជាការពិត។ ចូរយើងសរសេរនិយមន័យនៃលេខ - ក : │- ក│= (2) ចូរយើងប្រៀបធៀបសំណុំ (1) និង (2) ។ ជាក់ស្តែង និយមន័យនៃតម្លៃដាច់ខាតនៃលេខ កនិង - កផ្គូផ្គង។ អាស្រ័យហេតុនេះ │а│=│- а│
នៅពេលពិចារណាលើលក្ខណៈសម្បត្តិខាងក្រោម យើងនឹងដាក់កម្រិតខ្លួនយើងចំពោះការបង្កើតរបស់ពួកគេ ដោយសារភស្តុតាងរបស់ពួកគេត្រូវបានផ្តល់ឱ្យ អចលនទ្រព្យលេខ ២៖ តម្លៃដាច់ខាតនៃផលបូកនៃចំនួនកំណត់នៃចំនួនពិតមិនលើសពីផលបូកនៃតម្លៃដាច់ខាតនៃលក្ខខណ្ឌ៖ │а 1 + а 2 +…+ а n │ ≤│а 1 │ + │а 2 │ + … + │а n │ ទ្រព្យសម្បត្តិលេខ ៣៖ តម្លៃដាច់ខាតនៃភាពខុសគ្នារវាងចំនួនពិតពីរមិនត្រូវលើសពីផលបូកនៃតម្លៃដាច់ខាតរបស់វាទេ៖ │а - в│ ≤│а│+│в│ អចលនទ្រព្យលេខ ៤៖ តម្លៃដាច់ខាតនៃផលិតផលនៃចំនួនកំណត់នៃចំនួនពិតគឺស្មើនឹងផលិតផលនៃតម្លៃដាច់ខាតនៃកត្តា៖ │а·в│=│а│·│в│ អចលនទ្រព្យលេខ ៥៖ តម្លៃដាច់ខាតនៃកូតានៃចំនួនពិតគឺស្មើនឹងកូតានៃតម្លៃដាច់ខាតរបស់ពួកគេ៖

ផ្នែកទី 3. ការបកស្រាយធរណីមាត្រនៃគំនិតនៃម៉ូឌុលនៃចំនួនមួយ។

ចំនួនពិតនីមួយៗអាចត្រូវបានភ្ជាប់ជាមួយចំណុចនៅលើបន្ទាត់លេខ ដែលនឹងក្លាយជារូបភាពធរណីមាត្រនៃចំនួនពិតនេះ។ ចំណុចនីមួយៗនៅលើបន្ទាត់លេខត្រូវគ្នាទៅនឹងចម្ងាយរបស់វាពីប្រភពដើមពោលគឺឧ។ ប្រវែងនៃផ្នែកពីប្រភពដើមទៅចំណុចដែលបានផ្តល់ឱ្យ។ ចម្ងាយនេះតែងតែត្រូវបានចាត់ទុកថាជាតម្លៃមិនអវិជ្ជមាន។ ដូច្នេះប្រវែងនៃផ្នែកដែលត្រូវគ្នានឹងជាការបកស្រាយធរណីមាត្រនៃតម្លៃដាច់ខាតនៃចំនួនពិតដែលបានផ្តល់ឱ្យ។

រូបភាពធរណីមាត្រដែលបានបង្ហាញបញ្ជាក់យ៉ាងច្បាស់អំពីទ្រព្យសម្បត្តិលេខ 1 ពោលគឺឧ។ ម៉ូឌុលនៃលេខផ្ទុយគឺស្មើគ្នា។ ពីទីនេះសុពលភាពនៃសមភាពត្រូវបានយល់យ៉ាងងាយស្រួល៖ │х – а│= │а – x│ ។ ដំណោះស្រាយចំពោះសមីការ │x│= m ដែល m ≥ 0 គឺ x 1.2 = ± m ក៏កាន់តែច្បាស់។ ឧទាហរណ៍: 1) │х│= 4 x 1.2 = ± 4 2) │х − 3│= 1
x 1.2 = 2; ៤

ផ្នែកទី 4. ក្រាហ្វនៃអនុគមន៍ y = │x│

ដែននៃអនុគមន៍នេះគឺជាចំនួនពិតទាំងអស់។

ផ្នែកទី 5. អនុសញ្ញា។

នៅពេលអនាគត នៅពេលពិចារណាឧទាហរណ៍នៃការដោះស្រាយសមីការ អនុសញ្ញាខាងក្រោមនឹងត្រូវបានប្រើ៖ (-សញ្ញាប្រព័ន្ធ [-សញ្ញានៃចំនួនសរុប នៅពេលដោះស្រាយប្រព័ន្ធសមីការ (វិសមភាព) ចំនុចប្រសព្វនៃដំណោះស្រាយនៃសមីការ (វិសមភាព) ដែលរួមបញ្ចូលក្នុងប្រព័ន្ធត្រូវបានរកឃើញ។ នៅពេលដោះស្រាយសំណុំសមីការ (វិសមភាព) ការរួបរួមនៃដំណោះស្រាយដែលរួមបញ្ចូលក្នុងសំណុំសមីការ (វិសមភាព) ត្រូវបានរកឃើញ។

ជំពូកទី 2. ការដោះស្រាយសមីការដែលមានម៉ូឌុល។

នៅក្នុងជំពូកនេះ យើងនឹងពិនិត្យមើលវិធីសាស្ត្រពិជគណិតសម្រាប់ដោះស្រាយសមីការដែលមានម៉ូឌុលមួយ ឬច្រើន។

ផ្នែកទី 1. សមីការនៃទម្រង់ │F (x)│= m

សមីការនៃប្រភេទនេះត្រូវបានគេហៅថាសាមញ្ញបំផុត។ វាមានដំណោះស្រាយប្រសិនបើ m ≥ 0។ តាមនិយមន័យនៃម៉ូឌុល សមីការដើមគឺស្មើនឹងសំណុំនៃសមីការពីរ៖ │ ច(x)│=ម
ឧទាហរណ៍:
№1. ដោះស្រាយសមីការ៖ │7х − 2│= 9


ចម្លើយ៖ x 1 = - ១; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = −1; x 2 = −2 x (x + 3) = 0 x 1 = 0; x 2 = −3 ចម្លើយ៖ ផលបូកនៃឫសគឺ - ២.№3
│x 4 −5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 តំណាង x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – តម្លៃទាំងពីរបំពេញលក្ខខណ្ឌ m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 ចម្លើយ៖ ចំនួនឫសនៃសមីការ ៧. លំហាត់៖
№1. ដោះស្រាយសមីការ និងចង្អុលបង្ហាញផលបូកនៃឫស៖ │х - 5│= 3 №2 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញឫសតូច៖ │x 2 + x│= 0 №3 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញឫសធំ៖ │x 2 – 5x + 4│= 4 №4 .ដោះស្រាយសមីការ និងចង្អុលបង្ហាញឫសទាំងមូល៖ │2x 2 – 7x + 6│= 1 №5 .ដោះស្រាយសមីការ និងចង្អុលបង្ហាញចំនួនឫស៖ │x 4 – 13x 2 + 50│= 14

ផ្នែកទី 2. សមីការនៃទម្រង់ F(│х│) = m

អាគុយម៉ង់មុខងារនៅផ្នែកខាងឆ្វេងស្ថិតនៅក្រោមសញ្ញាម៉ូឌុល ហើយផ្នែកខាងស្តាំគឺឯករាជ្យនៃអថេរ។ ចូរយើងពិចារណាវិធីពីរយ៉ាងដើម្បីដោះស្រាយសមីការនៃប្រភេទនេះ។ 1 វិធី៖តាមនិយមន័យនៃតម្លៃដាច់ខាត សមីការដើមគឺស្មើនឹងការរួមបញ្ចូលគ្នានៃប្រព័ន្ធពីរ។ នៅក្នុងលក្ខខណ្ឌនីមួយៗត្រូវបានដាក់លើកន្សោម submodular ។ ច(│х│) =ម
ដោយសារអនុគមន៍ F(│x│) គឺសូម្បីតែនៅទូទាំងដែននៃនិយមន័យទាំងមូល ឫសនៃសមីការ F(x) = m និង F(- x) = m គឺជាគូនៃលេខផ្ទុយ។ ដូច្នេះវាគ្រប់គ្រាន់ហើយក្នុងការដោះស្រាយប្រព័ន្ធមួយ (នៅពេលពិចារណាឧទាហរណ៍នៅក្នុងវិធីនេះដំណោះស្រាយចំពោះប្រព័ន្ធមួយនឹងត្រូវបានផ្តល់ឱ្យ) ។ វិធីទី ២៖ការអនុវត្តវិធីសាស្រ្តនៃការណែនាំអថេរថ្មី។ ក្នុងករណីនេះ ការរចនា │x│= a ត្រូវបានណែនាំ ដែល a ≥ 0. វិធីសាស្រ្តនេះគឺមិនសូវមានពន្លឺនៅក្នុងការរចនា។
ឧទាហរណ៍: №1 . ដោះស្រាយសមីការ៖ 3x 2 – 4│x│= - 1 ចូរប្រើសេចក្តីផ្តើមនៃអថេរថ្មី។ ចូរយើងសម្គាល់ │x│= a ដែល a ≥ 0។ យើងទទួលបានសមីការ 3a 2 − 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 ត្រឡប់ទៅអថេរដើម៖ │ x│=1 និង │х│= 1/3 ។ សមីការនីមួយៗមានឫសពីរ។ ចម្លើយ៖ x 1 = 1; X 2 = - ១; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. ដោះស្រាយសមីការ៖ 5x 2 + 3│x│- 1 = 1/2 │x│ + 3x 2
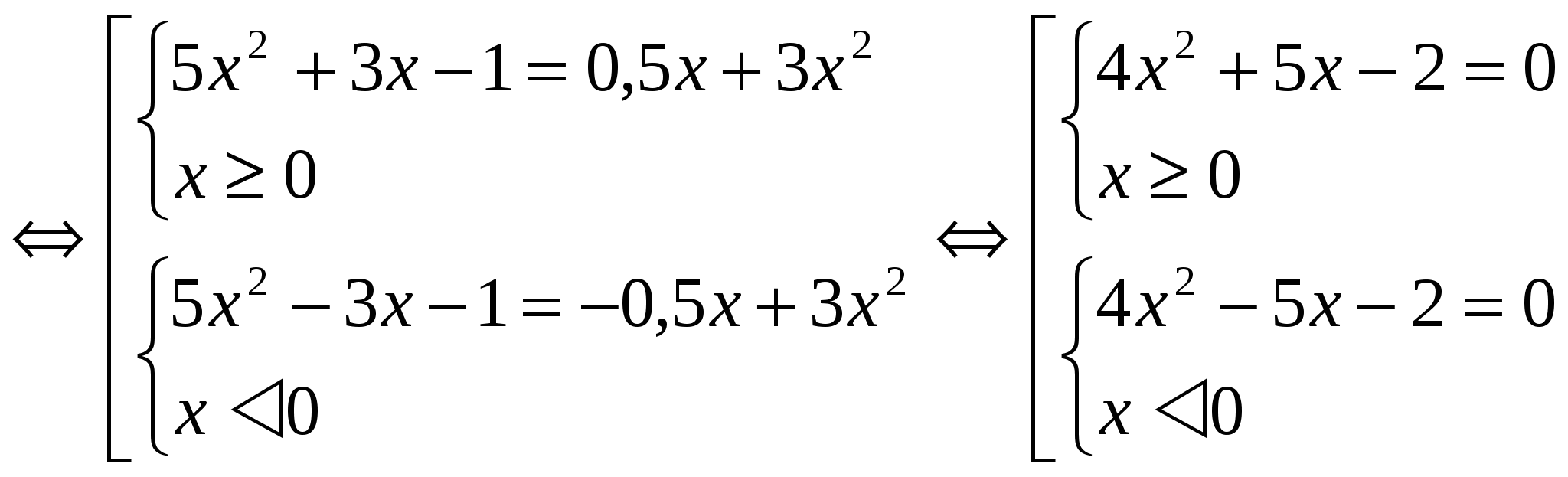ចូររកដំណោះស្រាយចំពោះប្រព័ន្ធទីមួយនៃចំនួនប្រជាជន៖ 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 ចំណាំថា x 2 មិនពេញចិត្តទេ លក្ខខណ្ឌ x ≥ 0. ដំណោះស្រាយប្រព័ន្ធទីពីរនឹងជាលេខទល់មុខនឹងតម្លៃ x 1 ។ ចម្លើយ៖ x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . ដោះស្រាយសមីការ៖ x 4 – │х│= 0 ចូរយើងសម្គាល់ │х│= a ដែល a ≥ 0 យើងទទួលបានសមីការ a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 ត្រឡប់ទៅអថេរដើមវិញ៖ │х│=0 និង │х│= 1 x = 0; ± ១ ចម្លើយ៖ x 1 = 0; X 2 = 1; X 3 = - 1.
លំហាត់៖ №6. ដោះស្រាយសមីការ៖ 2│х│ - 4.5 = 5 – 3 / 8 │х│ №7 . ដោះស្រាយសមីការ បង្ហាញចំនួនឫសក្នុងចម្លើយរបស់អ្នក៖ 3x 2 - 7│x│ + 2 = 0 №8 . ដោះស្រាយសមីការ បង្ហាញដំណោះស្រាយចំនួនគត់នៅក្នុងចម្លើយរបស់អ្នក៖ x 4 + │x│ - 2 = 0

ផ្នែកទី 3. សមីការនៃទម្រង់ │F(x)│ = G(x)

ផ្នែកខាងស្តាំនៃសមីការនៃប្រភេទនេះអាស្រ័យលើអថេរមួយ ហើយដូច្នេះវាមានដំណោះស្រាយប្រសិនបើផ្នែកខាងស្តាំគឺជាអនុគមន៍ G(x) ≥ 0។ សមីការដើមអាចដោះស្រាយបានតាមពីរវិធី : 1 វិធី៖ស្ដង់ដារ ដោយផ្អែកលើការបង្ហាញនៃម៉ូឌុលដោយផ្អែកលើនិយមន័យរបស់វា និងមានការផ្លាស់ប្តូរសមមូលទៅជាការរួមបញ្ចូលគ្នានៃប្រព័ន្ធពីរ។ │ ច(x)│ =ជី(X)

វិធីសាស្រ្តនេះអាចត្រូវបានប្រើដោយហេតុផលក្នុងករណីនៃកន្សោមស្មុគស្មាញសម្រាប់អនុគមន៍ G(x) និងស្មុគស្មាញតិចជាងសម្រាប់អនុគមន៍ F(x) ព្រោះវាត្រូវបានគេសន្មត់ថាវិសមភាពជាមួយអនុគមន៍ F(x) នឹងត្រូវបានដោះស្រាយ។ វិធីទី ២៖មាននៅក្នុងការផ្លាស់ប្តូរទៅជាប្រព័ន្ធសមមូលដែលលក្ខខណ្ឌមួយត្រូវបានដាក់នៅខាងស្តាំ។ │ ច(x)│= ជី(x)

វិធីសាស្ត្រនេះងាយស្រួលប្រើជាង ប្រសិនបើកន្សោមសម្រាប់អនុគមន៍ G(x) មានភាពស្មុគ្រស្មាញជាងអនុគមន៍ F(x) ចាប់តាំងពីដំណោះស្រាយចំពោះវិសមភាព G(x) ≥ 0 ត្រូវបានសន្មត់បន្ថែមលើករណី នៃម៉ូឌុលជាច្រើន វាត្រូវបានណែនាំឱ្យប្រើជម្រើសទីពីរ។ ឧទាហរណ៍: №1. ដោះស្រាយសមីការ៖ │x + 2│ = 6 −2x
(១ វិធី) ចម្លើយ៖ x = ១ 1 / 3 №2.
│х 2 − 2х − 1│ = 2·(x + 1)
(២ ផ្លូវ) ចម្លើយ៖ ផលិតផលឫសគឺ ៣.
№3. ដោះស្រាយសមីការ និងចង្អុលបង្ហាញផលបូកនៃឫសនៅក្នុងចម្លើយរបស់អ្នក៖
│x − 6│= x 2 − 5x + 9

ចម្លើយ៖ ផលបូកនៃឫសគឺ ៤។
លំហាត់៖ №9. │x + 4│= − 3x №10. ដោះស្រាយសមីការ បង្ហាញចំនួនដំណោះស្រាយក្នុងចម្លើយរបស់អ្នក៖ │x 2 + x − 1│ = 2x – 1 №11 . ដោះស្រាយសមីការ បង្ហាញផលិតផលនៃឫសនៅក្នុងចម្លើយរបស់អ្នក៖ │x + 3│ = x 2 + x – 6

ផ្នែកទី 4. សមីការនៃទម្រង់ │F(x)│= F(x) និង │F(x)│= - F(x)

សមីការនៃប្រភេទនេះជួនកាលត្រូវបានគេហៅថា "ស្អាតបំផុត" ។ ដោយសារផ្នែកខាងស្តាំនៃសមីការអាស្រ័យលើអថេរ ដំណោះស្រាយមានប្រសិនបើ ហើយប្រសិនបើផ្នែកខាងស្តាំមិនអវិជ្ជមាន។ ដូច្នេះសមីការដើមគឺស្មើនឹងវិសមភាព៖
│F(x)│= F(x) F(x) ≥ 0 និង │F(x)│= - F(x) F(x) ឧទាហរណ៍: №1 . ដោះស្រាយសមីការ បង្ហាញឫសចំនួនគត់តូចជាងនៅក្នុងចម្លើយរបស់អ្នក៖ │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0.6 ចម្លើយ៖ x = ១№2. ដោះស្រាយសមីការ បង្ហាញពីប្រវែងនៃចន្លោះពេលក្នុងចម្លើយរបស់អ្នក៖ │х 2 - 9│= 9 − x 2 x 2 − 9 ≤ 0 (x − 3) (x + 3) ≤ 0 [− 3; 3] ចម្លើយ៖ ប្រវែងនៃគម្លាតគឺ 6 ។№3 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញចំនួននៃដំណោះស្រាយចំនួនគត់នៅក្នុងចម្លើយរបស់អ្នក៖ │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] ចម្លើយ៖ ៤ ដំណោះស្រាយទាំងមូល។№4 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញឫសធំបំផុតនៅក្នុងចម្លើយរបស់អ្នក៖
│4 – x -
│ = 4 – x –
x 2 − 5x + 5 = 0 D = 5 x 1.2 =
≈ 1,4

ចម្លើយ៖ x = ៣.

លំហាត់៖ №12. ដោះស្រាយសមីការ ចង្អុលបង្ហាញឫសទាំងមូលនៅក្នុងចម្លើយ៖ │x 2 + 6x + 8│ = x 2 + 6x + 8 №13. ដោះស្រាយសមីការ បង្ហាញចំនួននៃដំណោះស្រាយចំនួនគត់នៅក្នុងចម្លើយរបស់អ្នក៖ │13x – x 2 – 36│+ x 2 – 13x + 36 = 0 №14. ដោះស្រាយសមីការនៅក្នុងចម្លើយរបស់អ្នក បង្ហាញចំនួនគត់ដែលមិនមែនជាឫសគល់នៃសមីការ

ផ្នែកទី 5. សមីការនៃទម្រង់ │F(x)│= │G(x)│

ដោយសារផ្នែកទាំងពីរនៃសមីការគឺមិនអវិជ្ជមាន ដំណោះស្រាយពាក់ព័ន្ធនឹងការពិចារណាលើករណីពីរ៖ កន្សោម submodular គឺស្មើគ្នា ឬផ្ទុយគ្នានៅក្នុងសញ្ញា។ ដូច្នេះសមីការដើមគឺស្មើនឹងការរួមបញ្ចូលគ្នានៃសមីការពីរ៖ │ ច(x)│= │ ជី(x)│
ឧទាហរណ៍: №1. ដោះស្រាយសមីការ ចង្អុលបង្ហាញឫសទាំងមូលនៅក្នុងចម្លើយរបស់អ្នក៖ │x + 3│=│2x - 1│
ចម្លើយ៖ ឫសទាំងមូល x = 4 ។№2. ដោះស្រាយសមីការ៖ │ x – x 2 – 1│ = │2x – 3 – x 2 │
ចម្លើយ៖ x = ២.№3 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញផលិតផលនៃឫសនៅក្នុងចម្លើយរបស់អ្នក៖




សមីការឫសគល់ 4x 2 + 2x – 1 = 0 x 1.2 = − 1±√5 / 4 ចម្លើយ៖ ផលិតផលឫសគឺ - ០.២៥ ។ លំហាត់៖ №15 . ដោះស្រាយសមីការ ហើយចង្អុលបង្ហាញដំណោះស្រាយទាំងមូលនៅក្នុងចម្លើយរបស់អ្នក៖ │x 2 – 3x + 2│= │x 2 + 6x – 1│ №16. ដោះស្រាយសមីការ ចង្អុលបង្ហាញឫសតូចជាងនៅក្នុងចម្លើយរបស់អ្នក៖ │5x - 3│=│7 - x│ №17 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញផលបូកនៃឫសនៅក្នុងចម្លើយរបស់អ្នក៖

ផ្នែកទី 6. ឧទាហរណ៍នៃការដោះស្រាយសមីការមិនស្តង់ដារ

នៅក្នុងផ្នែកនេះ យើងនឹងពិនិត្យមើលឧទាហរណ៍នៃសមីការមិនស្តង់ដារ នៅពេលដោះស្រាយដែលតម្លៃដាច់ខាតនៃកន្សោមត្រូវបានបង្ហាញតាមនិយមន័យ។ ឧទាហរណ៍:

№1. ដោះស្រាយសមីការ បង្ហាញផលបូកនៃឫសក្នុងចម្លើយរបស់អ្នក៖ x · │x│- 5x – 6 = 0
ចម្លើយ៖ ផលបូកនៃឫសគឺ ១ №2. . ដោះស្រាយសមីការ ចង្អុលបង្ហាញឫសតូចជាងនៅក្នុងចម្លើយរបស់អ្នក៖ x 2 - 4x ·
- 5 = 0
ចម្លើយ៖ ឫសតូច x = − ៥ ។ №3. ដោះស្រាយសមីការ៖

ចម្លើយ៖ x = −1 ។ លំហាត់៖ №18. ដោះស្រាយសមីការ និងចង្អុលបង្ហាញផលបូកនៃឫស៖ x · │3x + 5│= 3x 2 + 4x + 3
№19. ដោះស្រាយសមីការ៖ x 2 − 3x =

№20. ដោះស្រាយសមីការ៖

ផ្នែកទី 7. សមីការនៃទម្រង់ │F(x)│+│G(x)│=0

វាងាយស្រួលក្នុងការកត់សំគាល់ថានៅផ្នែកខាងឆ្វេងនៃសមីការនៃប្រភេទនេះគឺជាផលបូកនៃបរិមាណមិនអវិជ្ជមាន។ ដូច្នេះ សមីការដើមមានដំណោះស្រាយប្រសិនបើ និងលុះត្រាតែពាក្យទាំងពីរស្មើនឹងសូន្យក្នុងពេលតែមួយ។ សមីការគឺស្មើនឹងប្រព័ន្ធសមីការ៖ │ ច(x)│+│ ជី(x)│=0
ឧទាហរណ៍: №1 . ដោះស្រាយសមីការ៖
ចម្លើយ៖ x = ២. №2. ដោះស្រាយសមីការ៖ ចម្លើយ៖ x = ១. លំហាត់៖ №21. ដោះស្រាយសមីការ៖ №22 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញផលបូកនៃឫសនៅក្នុងចម្លើយរបស់អ្នក៖ №23 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញចំនួននៃដំណោះស្រាយនៅក្នុងចម្លើយរបស់អ្នក៖

ផ្នែកទី 8. សមីការនៃទម្រង់ │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

ដើម្បីដោះស្រាយសមីការនៃប្រភេទនេះ វិធីសាស្ត្រចន្លោះពេលត្រូវបានប្រើ។ ប្រសិនបើយើងដោះស្រាយវាដោយការពង្រីកជាបន្តបន្ទាប់នៃម៉ូឌុល យើងទទួលបាន នសំណុំនៃប្រព័ន្ធ ដែលស្មុគស្មាញ និងរអាក់រអួល។ ចូរយើងពិចារណាអំពីក្បួនដោះស្រាយចន្លោះពេល៖ ១). ស្វែងរកតម្លៃអថេរ Xដែលម៉ូឌុលនីមួយៗស្មើនឹងសូន្យ (សូន្យនៃកន្សោមម៉ូឌុល)៖
២). សម្គាល់​តម្លៃ​ដែល​បាន​រក​ឃើញ​នៅ​លើ​បន្ទាត់​លេខ ដែល​ត្រូវ​បាន​បែង​ចែក​ជា​ចន្លោះ​ពេល (ចំនួន​ចន្លោះ​ពេល​រៀង​គ្នា​ស្មើ​នឹង ន+1 ) ៣). កំណត់ជាមួយនឹងសញ្ញាណាមួយដែលម៉ូឌុលនីមួយៗត្រូវបានបង្ហាញនៅចន្លោះពេលនីមួយៗដែលទទួលបាន (នៅពេលបង្កើតដំណោះស្រាយអ្នកអាចប្រើបន្ទាត់លេខសម្គាល់សញ្ញានៅលើវា) 4) ។ សមីការដើមគឺស្មើនឹងសរុប ន+1 ប្រព័ន្ធនីមួយៗ ដែលសមាជិកភាពរបស់អថេរត្រូវបានចង្អុលបង្ហាញ Xចន្លោះពេលមួយ។ ឧទាហរណ៍: №1 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញឫសធំបំផុតនៅក្នុងចម្លើយរបស់អ្នក៖
១). ចូររកលេខសូន្យនៃកន្សោម submodular: x = 2; x = −3 ២). ចូរសម្គាល់តម្លៃដែលបានរកឃើញនៅលើបន្ទាត់លេខ ហើយកំណត់ជាមួយនឹងសញ្ញាអ្វីដែលម៉ូឌុលនីមួយៗត្រូវបានបង្ហាញនៅលើចន្លោះពេលលទ្ធផល៖
x – 2 x – 2 x – 2 – - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- គ្មានដំណោះស្រាយ សមីការមានឫសពីរ។ ចម្លើយ៖ ឫសធំបំផុត x = 2 ។ №2. ដោះស្រាយសមីការ និងផ្តល់ឫសគល់ទាំងមូលនៅក្នុងចម្លើយរបស់អ្នក៖
១). ចូររកលេខសូន្យនៃកន្សោម submodular: x = 1.5; x = − 1 2). ចូរសម្គាល់តម្លៃដែលបានរកឃើញនៅលើបន្ទាត់លេខ ហើយកំណត់ជាមួយនឹងសញ្ញាអ្វីដែលម៉ូឌុលនីមួយៗត្រូវបានបង្ហាញនៅលើចន្លោះពេលលទ្ធផល៖ x + 1 x + 1 x + 1 - + +
-1 1.5 x 2x – 3 2x – 3 2x – 3 - - +
3).
ប្រព័ន្ធចុងក្រោយមិនមានដំណោះស្រាយទេ ដូច្នេះសមីការមានឫសពីរ។ នៅពេលដោះស្រាយសមីការ អ្នកគួរតែយកចិត្តទុកដាក់លើសញ្ញា "-" នៅពីមុខម៉ូឌុលទីពីរ។ ចម្លើយ៖ ឫសទាំងមូល x = ៧ ។ №3. ដោះស្រាយសមីការ ចង្អុលបង្ហាញផលបូកនៃឫសក្នុងចម្លើយរបស់អ្នក៖ ១). ចូររកលេខសូន្យនៃកន្សោម submodular: x = 5; x = 1; x = − 2 ២). ចូរសម្គាល់តម្លៃដែលបានរកឃើញនៅលើបន្ទាត់លេខ ហើយកំណត់ជាមួយនឹងសញ្ញាអ្វីដែលម៉ូឌុលនីមួយៗត្រូវបានបង្ហាញនៅចន្លោះពេលលទ្ធផល៖ x – 5 x – 5 x – 5 x – 5 - - - +
−2 1 5 x x – 1 x – 1 x – 1 x – 1 – − + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
សមីការមានឫសពីរ x = 0 និង 2 ។ ចម្លើយ៖ ផលបូកនៃឫសគឺ ២. №4 . ដោះស្រាយសមីការ៖ ១). ចូរយើងរកលេខសូន្យនៃកន្សោម submodular: x = 1; x = 2; x = 3. 2). អនុញ្ញាតឱ្យយើងកំណត់ជាមួយនឹងសញ្ញាអ្វីដែលម៉ូឌុលនីមួយៗត្រូវបានបង្ហាញនៅលើចន្លោះពេលលទ្ធផល។ ៣).
ចូរយើងបញ្ចូលគ្នានូវដំណោះស្រាយនៃប្រព័ន្ធបីដំបូង។ ចម្លើយ៖ ; x = ៥.
លំហាត់៖ №24. ដោះស្រាយសមីការ៖
№25. ដោះស្រាយសមីការ និងចង្អុលបង្ហាញផលបូកនៃឫសនៅក្នុងចម្លើយរបស់អ្នក៖ №26. ដោះស្រាយសមីការ និងចង្អុលបង្ហាញឫសតូចជាងនៅក្នុងចម្លើយរបស់អ្នក៖ №27. ដោះស្រាយសមីការ និងចង្អុលបង្ហាញឫសធំជាងនៅក្នុងចម្លើយរបស់អ្នក៖

ផ្នែកទី 9. សមីការដែលមានម៉ូឌុលជាច្រើន។

សមីការដែលមានម៉ូឌុលច្រើនសន្មតថាវត្តមាននៃតម្លៃដាច់ខាតនៅក្នុងកន្សោមម៉ូឌុល។ គោលការណ៍ជាមូលដ្ឋានសម្រាប់ការដោះស្រាយសមីការនៃប្រភេទនេះគឺការបង្ហាញជាបន្តបន្ទាប់នៃម៉ូឌុល ដោយចាប់ផ្តើមជាមួយ "ខាងក្រៅ" មួយ។ ក្នុងអំឡុងពេលនៃដំណោះស្រាយ បច្ចេកទេសដែលបានពិភាក្សានៅក្នុងផ្នែកលេខ 1 លេខ 3 ត្រូវបានប្រើប្រាស់។

ឧទាហរណ៍: №1. ដោះស្រាយសមីការ៖
ចម្លើយ៖ x = 1; - ដប់មួយ №2. ដោះស្រាយសមីការ៖
ចម្លើយ៖ x = 0; ៤; - ៤. №3. ដោះស្រាយសមីការ និងចង្អុលបង្ហាញផលិតផលនៃឫសនៅក្នុងចម្លើយរបស់អ្នក៖
ចម្លើយ៖ ផលិតផលឫសគឺ ៨. №4. ដោះស្រាយសមីការ៖
ចូរយើងបង្ហាញពីសមីការនៃចំនួនប្រជាជន (1) និង (2) ហើយពិចារណាដំណោះស្រាយចំពោះពួកវានីមួយៗដាច់ដោយឡែកពីគ្នា ដើម្បីភាពងាយស្រួលនៃការរចនា។ ដោយសារសមីការទាំងពីរមានម៉ូឌុលច្រើនជាងមួយ វាកាន់តែងាយស្រួលក្នុងការអនុវត្តការផ្លាស់ប្តូរសមមូលទៅសំណុំនៃប្រព័ន្ធ។ (1)

(2)


ចម្លើយ៖
លំហាត់៖ №36. ដោះស្រាយសមីការ បង្ហាញផលបូកនៃឫសក្នុងចម្លើយរបស់អ្នក៖ 5 │3x-5│ = 25 x №37. ដោះស្រាយសមីការប្រសិនបើមានឫសច្រើនជាងមួយ បង្ហាញផលបូកនៃឫសនៅក្នុងចម្លើយរបស់អ្នក៖ │x + 2│ x – 3x – 10 = 1 №38. ដោះស្រាយសមីការ៖ 3 │2х −4│ = 9 │х│ №39. ដោះស្រាយសមីការ ចម្លើយរបស់អ្នកបង្ហាញពីចំនួនឫសក្នុងមួយ៖ 2 │ sin x│ = √2 №40 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញចំនួនឫសនៅក្នុងចម្លើយរបស់អ្នក៖

ផ្នែកទី 3. សមីការលោការីត។

មុននឹងដោះស្រាយសមីការខាងក្រោម ចាំបាច់ត្រូវពិនិត្យមើលលក្ខណៈសម្បត្តិរបស់លោការីត និងអនុគមន៍លោការីត។ ឧទាហរណ៍: №1. ដោះស្រាយសមីការ ចង្អុលបង្ហាញផលិតផលនៃឫសនៅក្នុងចម្លើយរបស់អ្នក៖ កំណត់ហេតុ 2 (x+1) 2 + កំណត់ហេតុ 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ − 1

ករណីទី 1៖ ប្រសិនបើ x ≥ − 1 បន្ទាប់មក log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – បំពេញលក្ខខណ្ឌ x ≥ - 1 2 ករណី៖ ប្រសិនបើ x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 កំណត់ហេតុ 2 (-(x+1) 3) = កំណត់ហេតុ 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = − 5– បំពេញលក្ខខណ្ឌ x - 1
ចម្លើយ៖ ផលិតផលនៃឫសគឺ - ១៥ ។
№2. ដោះស្រាយសមីការ ចង្អុលបង្ហាញផលបូកនៃឫសនៅក្នុងចម្លើយរបស់អ្នក៖ lg
O.D.Z.

ចម្លើយ៖ ផលបូកនៃឫសគឺ ០.៥។
№3. ដោះស្រាយសមីការ៖ កំណត់ហេតុ ៥
O.D.Z.

ចម្លើយ៖ x = ៩ ។ №4. ដោះស្រាយសមីការ៖ │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 ចូរយើងប្រើរូបមន្តសម្រាប់ផ្លាស់ទីទៅមូលដ្ឋានផ្សេងទៀត។ │2 - កំណត់ហេតុ 5 x│+ 3 = │1 + កំណត់ហេតុ 5 x│
│2 - log 5 x│- │1 + log 5 x│= − 3 ចូររកលេខសូន្យនៃកន្សោមម៉ូឌុល៖ x = 25; x = លេខទាំងនេះបែងចែកជួរនៃតម្លៃដែលអាចទទួលយកបានទៅជាបីចន្លោះ ដូច្នេះសមីការគឺស្មើនឹងសំណុំនៃប្រព័ន្ធបី។
ចម្លើយ :)