Resolvendo equações e desigualdades com módulo muitas vezes causa dificuldades. No entanto, se você entender bem o que é o valor absoluto de um número, E como expandir corretamente expressões contendo um sinal de módulo, então a presença na equação expressão sob o sinal do módulo, deixa de ser um obstáculo à sua solução.

Um pouco de teoria. Cada número possui duas características: o valor absoluto do número e seu sinal.

Por exemplo, o número +5, ou simplesmente 5, tem um sinal “+” e um valor absoluto de 5.

O número -5 possui um sinal “-” e um valor absoluto de 5.

Os valores absolutos dos números 5 e -5 são 5.

O valor absoluto de um número x é chamado de módulo do número e é denotado por |x|.

Como vemos, o módulo de um número é igual ao próprio número se este número for maior ou igual a zero, e a este número com o sinal oposto se este número for negativo.

O mesmo se aplica a quaisquer expressões que apareçam sob o sinal de módulo.

A regra de expansão do módulo é semelhante a esta:

|f(x)|= f(x) se f(x) ≥ 0, e

|f(x)|= - f(x), se f(x)< 0

Por exemplo |x-3|=x-3, se x-3≥0 e |x-3|=-(x-3)=3-x, se x-3<0.

Para resolver uma equação contendo uma expressão sob o sinal de módulo, você deve primeiro expandir um módulo de acordo com a regra de expansão de módulo.

Então nossa equação ou desigualdade se torna em duas equações diferentes existentes em dois intervalos numéricos diferentes.

Existe uma equação em um intervalo numérico no qual a expressão sob o sinal do módulo é não negativa.

E a segunda equação existe no intervalo em que a expressão sob o sinal do módulo é negativa.

Vejamos um exemplo simples.

Vamos resolver a equação:

|x-3|=-x 2 +4x-3

1. Vamos abrir o módulo.

|x-3|=x-3, se x-3≥0, ou seja, se x≥3

|x-3|=-(x-3)=3-x se x-3<0, т.е. если х<3

2. Recebemos dois intervalos numéricos: x≥3 e x<3.

Vamos considerar em quais equações a equação original é transformada em cada intervalo:

A) Para x≥3 |x-3|=x-3, e nosso ferimento tem a forma:

Atenção! Esta equação existe apenas no intervalo x≥3!

Vamos abrir os colchetes e apresentar termos semelhantes:

e resolva esta equação.

Esta equação tem raízes:

x 1 =0, x 2 =3

Atenção! como a equação x-3=-x 2 +4x-3 existe apenas no intervalo x≥3, estamos interessados ​​apenas nas raízes que pertencem a esse intervalo. Esta condição é satisfeita apenas por x 2 =3.

B) Em x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

Atenção! Esta equação existe apenas no intervalo x<3!

Vamos abrir os colchetes e apresentar termos semelhantes. Obtemos a equação:

x 1 =2, x 2 =3

Atenção! já que a equação 3-x=-x 2 +4x-3 existe apenas no intervalo x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

Então: do primeiro intervalo tiramos apenas a raiz x=3, do segundo - a raiz x=2.

O módulo é o valor absoluto da expressão. Para indicar de alguma forma um módulo, costuma-se usar colchetes. O valor entre colchetes pares é o valor obtido do módulo. O processo de resolução de qualquer módulo consiste em abrir aqueles colchetes bem retos, que em linguagem matemática são chamados de colchetes modulares. Sua divulgação ocorre de acordo com um certo número de regras. Além disso, na ordem de resolução dos módulos, encontram-se os conjuntos de valores daquelas expressões que estavam entre colchetes modulares. Na maioria dos casos, o módulo é expandido de tal forma que a expressão que era submodular recebe valores positivos e negativos, incluindo o valor zero. Se partirmos das propriedades estabelecidas do módulo, então no processo são compiladas várias equações ou desigualdades da expressão original, que então precisam ser resolvidas. Vamos descobrir como resolver módulos.

Processo de solução

A resolução de um módulo começa escrevendo a equação original com o módulo. Para responder à questão de como resolver equações com módulo, você precisa abri-lo completamente. Para resolver tal equação, o módulo é expandido. Todas as expressões modulares devem ser consideradas. É necessário determinar em quais valores das incógnitas incluídas em sua composição a expressão modular entre colchetes torna-se zero. Para isso, basta igualar a expressão entre colchetes modulares a zero e depois calcular a solução da equação resultante. Os valores encontrados devem ser registrados. Da mesma forma, você também precisa determinar o valor de todas as variáveis ​​desconhecidas para todos os módulos desta equação. A seguir, é necessário determinar e considerar todos os casos de existência de variáveis ​​​​em expressões quando são diferentes do valor zero. Para fazer isso, você precisa escrever algum sistema de desigualdades correspondente a todos os módulos da desigualdade original. As desigualdades devem ser escritas de forma que cubram todos os valores disponíveis e possíveis para uma variável encontrada na reta numérica. Então você precisa desenhar esta mesma reta numérica para visualização, na qual posteriormente plotar todos os valores obtidos.

Quase tudo agora pode ser feito na Internet. O módulo não foge à regra. Você pode resolvê-lo online em um dos muitos recursos modernos. Todos os valores da variável que estão no módulo zero serão uma restrição especial que será utilizada no processo de resolução da equação modular. Na equação original, você precisa abrir todos os colchetes modulares disponíveis, enquanto altera o sinal da expressão para que os valores da variável desejada coincidam com os valores que são visíveis na reta numérica. A equação resultante deve ser resolvida. O valor da variável que será obtida durante a resolução da equação deve ser verificado em relação à limitação especificada pelo próprio módulo. Se o valor da variável satisfizer totalmente a condição, então ela está correta. Todas as raízes que serão obtidas durante a solução da equação, mas que não se enquadram nas restrições, devem ser descartadas.

Escola Secundária MBOU nº 17, Ivanovo

« Equações com módulo"
Desenvolvimento metodológico

Compilado

professor de matemática

Lebedeva N.V.

20010

Nota explicativa

Capítulo 1 Introdução

Seção 2. Propriedades básicas Seção 3. Interpretação geométrica do conceito de módulo de um número Seção 4. Gráfico da função y = |x| Seção 5. Convenções

Capítulo 2. Resolvendo equações contendo um módulo

Seção 1. Equações da forma |F(x)| = m (mais simples) Seção 2. Equações da forma F(|x|) = m Seção 3. Equações da forma |F(x)| =G(x) Seção 4. Equações da forma |F(x)| = ± F(x) (mais bonito) Seção 5. Equações da forma |F(x)| = |G(x)| Seção 6. Exemplos de resolução de equações não padronizadas Seção 7. Equações da forma |F(x)| + |G(x)| = 0 Seção 8. Equações da forma |a 1 x ± b 1 | ± |a 2 x ± b 2 | ± …|a n x ± em n | =m Seção 9. Equações contendo vários módulos

Capítulo 3. Exemplos de resolução de várias equações com módulo.

Seção 1. Equações trigonométricas Seção 2. Equações exponenciais Seção 3. Equações logarítmicas Seção 4. Equações irracionais Seção 5. Tarefas avançadas Respostas aos exercícios Bibliografia

Nota explicativa.

O conceito de valor absoluto (módulo) de um número real é uma de suas características essenciais. Este conceito é difundido em vários setores das ciências físicas, matemáticas e técnicas. Na prática de ensino de cursos de matemática em escolas secundárias de acordo com o Programa do Ministério da Defesa da Federação Russa, o conceito de “valor absoluto de um número” é encontrado repetidamente: na 6ª série, a definição de um módulo e seu significado geométrico é apresentado; na 8ª série, forma-se o conceito de erro absoluto, considera-se a solução das equações e desigualdades mais simples contendo um módulo e estudam-se as propriedades da raiz quadrada aritmética; no 11º ano o conceito encontra-se na seção “Raiz n-º grau." A experiência de ensino mostra que os alunos muitas vezes encontram dificuldades na resolução de tarefas que exigem o conhecimento desta matéria, e muitas vezes as saltam sem começar a concluí-las. Os textos dos trabalhos de exame dos cursos do 9.º e 11.º ano também incluem trabalhos semelhantes. Além disso, os requisitos que as universidades impõem aos diplomados são diferentes, nomeadamente, a um nível superior aos requisitos do currículo escolar. Para a vida na sociedade moderna, a formação de um estilo matemático de pensamento, manifestado em certas habilidades mentais, é muito importante. No processo de resolução de problemas com módulos, é necessária a capacidade de utilizar técnicas como generalização e especificação, análise, classificação e sistematização e analogia. A resolução de tais tarefas permite testar seu conhecimento das principais seções do curso escolar, o nível de pensamento lógico e as habilidades iniciais de pesquisa. Este trabalho é dedicado a uma das seções - resolução de equações contendo um módulo. É composto por três capítulos. O primeiro capítulo apresenta conceitos básicos e as considerações teóricas mais importantes. O segundo capítulo propõe nove tipos principais de equações contendo um módulo, discute métodos para resolvê-las e examina exemplos de diferentes níveis de complexidade. O terceiro capítulo oferece equações mais complexas e não padronizadas (trigonométricas, exponenciais, logarítmicas e irracionais). Para cada tipo de equação existem exercícios para resolução independente (respostas e instruções estão em anexo). O principal objetivo deste trabalho é prestar assistência metodológica aos professores na preparação das aulas e na organização de disciplinas optativas. O material também pode ser utilizado como auxílio didático para alunos do ensino médio. As tarefas propostas no trabalho são interessantes e nem sempre fáceis de resolver, o que permite tornar mais consciente a motivação educacional dos alunos, testar as suas capacidades e aumentar o nível de preparação dos egressos para o ingresso nas universidades. Uma seleção diferenciada dos exercícios propostos envolve a transição do nível reprodutivo de domínio do material para o criativo, bem como a oportunidade de ensinar como aplicar seus conhecimentos na resolução de problemas atípicos.

Capítulo 1 Introdução.

Seção 1. Determinação do valor absoluto .

Definição : O valor absoluto (módulo) de um número real A um número não negativo é chamado: A ou -A. Designação: │ A │ A entrada diz o seguinte: “módulo do número a” ou “valor absoluto do número a”

│ a, se a > 0

│a│ = │ 0, se a = 0 (1)

│ - e, se um
Exemplos: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Expanda o módulo de expressão:

a) │x - 8│, se x > 12 b) │2x + 3│, se x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

Seção 2. Propriedades básicas.

Consideremos as propriedades básicas do valor absoluto. Propriedade nº 1: Os números opostos têm módulos iguais, ou seja, │а│=│-à│ Vamos mostrar que a igualdade é verdadeira. Vamos escrever a definição do número - A : │- uma│= (2) Vamos comparar os conjuntos (1) e (2). Obviamente, as definições dos valores absolutos dos números A E - A combinar. Por isso, │а│=│-à│
Ao considerar as seguintes propriedades, nos limitaremos à sua formulação, uma vez que sua prova é dada em Propriedade nº 2: O valor absoluto da soma de um número finito de números reais não excede a soma dos valores absolutos dos termos: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ +… + │а n │ Propriedade nº 3: O valor absoluto da diferença entre dois números reais não excede a soma de seus valores absolutos: │а - в│ ≤│а│+│в│ Propriedade nº 4: O valor absoluto do produto de um número finito de números reais é igual ao produto dos valores absolutos dos fatores: │а·в│=│а│·│в│ Propriedade nº 5: O valor absoluto do quociente dos números reais é igual ao quociente dos seus valores absolutos:

Seção 3. Interpretação geométrica do conceito de módulo de um número.

Cada número real pode ser associado a um ponto da reta numérica, que será uma imagem geométrica desse número real. Cada ponto na reta numérica corresponde à sua distância da origem, ou seja, o comprimento do segmento desde a origem até um determinado ponto. Esta distância é sempre considerada como um valor não negativo. Portanto, o comprimento do segmento correspondente será a interpretação geométrica do valor absoluto de um determinado número real

A ilustração geométrica apresentada confirma claramente a propriedade nº 1, ou seja, os módulos de números opostos são iguais. A partir daqui a validade da igualdade é facilmente compreendida: │х – а│= │а – x│. A solução para a equação │x│= m, onde m ≥ 0, ou seja, x 1,2 = ± m, também se torna mais óbvia. Exemplos: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; 4

Seção 4. Gráfico da função y = │x│

O domínio desta função são todos os números reais.

Seção 5. Convenções.

No futuro, ao considerar exemplos de resolução de equações, serão utilizadas as seguintes convenções: ( - sinal do sistema [ - sinal da totalidade Ao resolver um sistema de equações (desigualdades), encontra-se a intersecção das soluções das equações (desigualdades) incluídas no sistema. Ao resolver um conjunto de equações (desigualdades), encontra-se a união das soluções incluídas no conjunto de equações (desigualdades).

Capítulo 2. Resolvendo equações contendo um módulo.

Neste capítulo veremos métodos algébricos para resolver equações contendo um ou mais módulos.

Seção 1. Equações da forma │F (x)│= m

Uma equação deste tipo é chamada de mais simples. Tem solução se e somente se m ≥ 0. Pela definição do módulo, a equação original é equivalente a um conjunto de duas equações: │ F(x)│=eu
Exemplos:
№1. Resolva a equação: │7х - 2│= 9


Resposta: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x2 = -3 Resposta: a soma das raízes é -2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 denota x 2 = m, m ≥ 0 x = 0; ±√5m 2 – 5m + 4 = 0m = 1; 4 – ambos os valores satisfazem a condição m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Resposta: número de raízes da equação 7. Exercícios:
№1. Resolva a equação e indique a soma das raízes: │х - 5│= 3 №2 . Resolva a equação e indique a raiz menor: │x 2 + x│= 0 №3 . Resolva a equação e indique a raiz maior: │x 2 – 5x + 4│= 4 №4 .Resolva a equação e indique a raiz inteira: │2x 2 – 7x + 6│= 1 №5 .Resolva a equação e indique o número de raízes: │x 4 – 13x 2 + 50│= 14

Seção 2. Equações da forma F(│х│) = m

O argumento da função no lado esquerdo está sob o sinal do módulo e o lado direito é independente da variável. Vamos considerar duas maneiras de resolver equações desse tipo. 1 maneira: Por definição de valor absoluto, a equação original equivale à combinação de dois sistemas. Em cada um deles uma condição é imposta a uma expressão submodular. F(│х│) =eu
Como a função F(│x│) é par em todo o domínio de definição, as raízes das equações F(x) = m e F(- x) = m são pares de números opostos. Portanto, basta resolver um dos sistemas (ao considerar exemplos desta forma, será dada a solução para um sistema). Método 2: Aplicação do método de introdução de uma nova variável. Neste caso, é introduzida a designação │x│= a, onde a ≥ 0. Este método é menos volumoso em design.
Exemplos: №1 . Resolva a equação: 3x 2 – 4│x│= - 1 Vamos usar a introdução de uma nova variável. Vamos denotar │x│= a, onde a ≥ 0. Obtemos a equação 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1/3 Retorne à variável original: │ x│=1 e │х│= 1/3. Cada equação tem duas raízes. Resposta: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Resolva a equação: 5x 2 + 3│x│- 1 = 1/2 │x│ + 3x 2
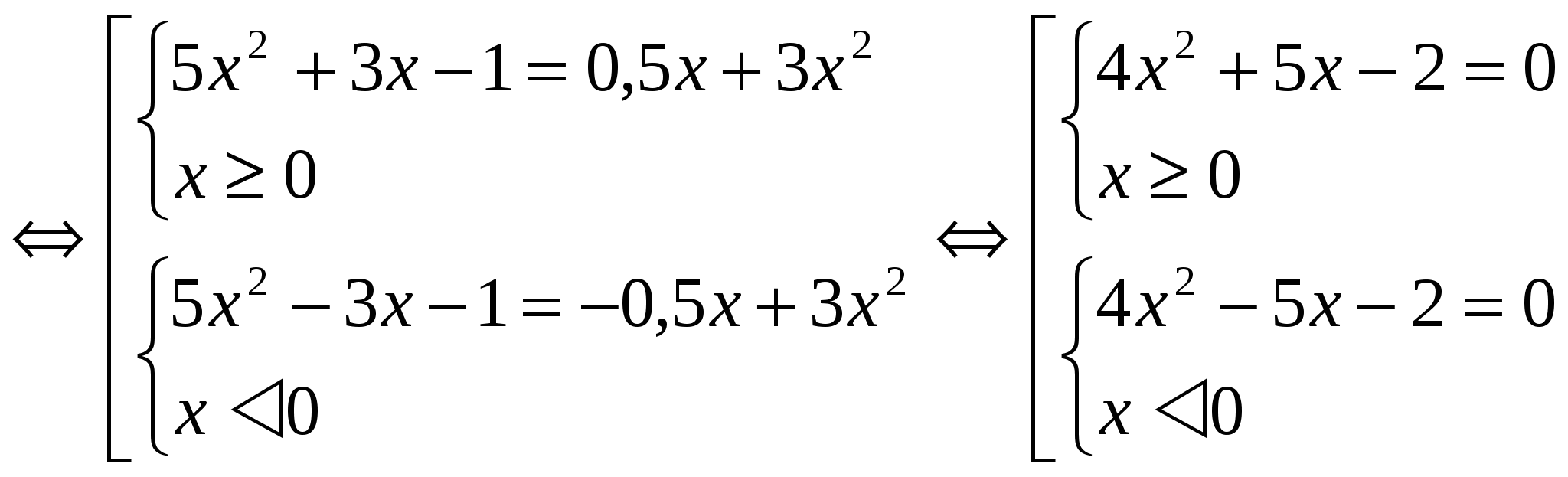Vamos encontrar a solução para o primeiro sistema da população: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Observe que x 2 não satisfaz a condição x ≥ 0. Solução o segundo sistema será o número oposto ao valor x 1. Resposta: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Resolva a equação: x 4 – │х│= 0 Vamos denotar │х│= a, onde a ≥ 0. Obtemos a equação a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Retorna à variável original: │х│=0 e │х│= 1 x = 0; ± 1 Resposta: x 1 = 0; X 2 = 1; X 3 = - 1.
Exercícios: №6. Resolva a equação: 2│х│ - 4,5 = 5 – 3/8 │х│ №7 . Resolva a equação, indique o número de raízes em sua resposta: 3x 2 - 7│x│ + 2 = 0 №8 . Resolva a equação, indique soluções inteiras em sua resposta: x 4 + │x│ - 2 = 0

Seção 3. Equações da forma │F(x)│ = G(x)

O lado direito de uma equação deste tipo depende de uma variável e, portanto, tem solução se e somente se o lado direito for uma função G(x) ≥ 0. A equação original pode ser resolvida de duas maneiras : 1 maneira: Padrão, baseado na divulgação de um módulo com base na sua definição e consiste em uma transição equivalente para uma combinação de dois sistemas. │ F(x)│ =G(X)

Este método pode ser utilizado racionalmente no caso de uma expressão complexa para a função G(x) e uma menos complexa para a função F(x), uma vez que se assume que as desigualdades com a função F(x) serão resolvidas. Método 2: Consiste na transição para um sistema equivalente em que uma condição é imposta ao lado direito. │ F(x)│= G(x)

Este método é mais conveniente de usar se a expressão para a função G(x) for menos complexa do que para a função F(x), uma vez que a solução para a desigualdade G(x) ≥ 0 é assumida além disso, no caso. de vários módulos, recomenda-se utilizar a segunda opção. Exemplos: №1. Resolva a equação: │x + 2│= 6 -2x
(1 via) Resposta: x = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(x + 1)
(2 maneiras) Resposta: O produto das raízes é 3.
№3. Resolva a equação e indique a soma das raízes em sua resposta:
│x - 6│= x 2 - 5x + 9

Resposta: a soma das raízes é 4.
Exercícios: №9. │x + 4│= -3x №10. Resolva a equação, indique o número de soluções em sua resposta:│x 2 + x - 1│= 2x – 1 №11 . Resolva a equação, indique o produto das raízes em sua resposta:│x + 3│= x 2 + x – 6

Seção 4. Equações da forma │F(x)│= F(x) e │F(x)│= - F(x)

Equações desse tipo são às vezes chamadas de “as mais bonitas”. Como o lado direito das equações depende da variável, existem soluções se e somente se o lado direito for não negativo. Portanto, as equações originais são equivalentes às desigualdades:
│F(x)│= F(x) F(x) ≥ 0 e │F(x)│= - F(x) F(x) Exemplos: №1 . Resolva a equação, indique a raiz inteira menor em sua resposta: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Resposta: x = 1№2. Resolva a equação, indique a duração do intervalo em sua resposta: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Resposta: o comprimento da lacuna é 6.№3 . Resolva a equação e indique o número de soluções inteiras em sua resposta: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Resposta: 4 soluções completas.№4 . Resolva a equação e indique a maior raiz em sua resposta:
│4 – x -
│= 4 – x –
x 2 – 5x + 5 = 0 D = 5 x 1,2 =
≈ 1,4

Resposta: x = 3.

Exercícios: №12. Resolva a equação, indique a raiz inteira na resposta: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Resolva a equação, indique o número de soluções inteiras em sua resposta: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Resolva a equação; em sua resposta, indique um número inteiro que não seja a raiz da equação:

Seção 5. Equações da forma │F(x)│= │G(x)│

Como ambos os lados da equação são não negativos, a solução envolve considerar dois casos: expressões submodulares têm sinais iguais ou opostos. Portanto, a equação original é equivalente à combinação de duas equações: │ F(x)│= │ G(x)│
Exemplos: №1. Resolva a equação, indique a raiz inteira em sua resposta: │x + 3│=│2x - 1│
Resposta: raiz inteira x = 4.№2. Resolva a equação: │ x – x 2 - 1│=│2x – 3 – x 2 │
Resposta: x = 2.№3 . Resolva a equação e indique o produto das raízes na sua resposta:




Equações raiz 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5/4 Resposta: o produto das raízes é – 0,25. Exercícios: №15 . Resolva a equação e indique a solução completa em sua resposta: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Resolva a equação, indique a raiz menor em sua resposta:│5x - 3│=│7 - x│ №17 . Resolva a equação e indique a soma das raízes em sua resposta:

Seção 6. Exemplos de resolução de equações não padronizadas

Nesta seção veremos exemplos de equações não padronizadas, ao resolver as quais o valor absoluto da expressão é revelado por definição. Exemplos:

№1. Resolva a equação, indique a soma das raízes em sua resposta: x · │x│- 5x – 6 = 0
Resposta: a soma das raízes é 1 №2. . Resolva a equação, indique a raiz menor em sua resposta: x 2 - 4x ·
- 5 = 0
Resposta: raiz menor x = - 5. №3. Resolva a equação:

Resposta: x = -1. Exercícios: №18. Resolva a equação e indique a soma das raízes: x · │3x + 5│= 3x 2 + 4x + 3
№19. Resolva a equação: x 2 – 3x =

№20. Resolva a equação:

Seção 7. Equações da forma │F(x)│+│G(x)│=0

É fácil perceber que no lado esquerdo da equação desse tipo está a soma das quantidades não negativas. Portanto, a equação original tem solução se e somente se ambos os termos forem iguais a zero ao mesmo tempo. A equação é equivalente ao sistema de equações: │ F(x)│+│ G(x)│=0
Exemplos: №1 . Resolva a equação:
Resposta: x = 2. №2. Resolva a equação: Resposta: x = 1. Exercícios: №21. Resolva a equação: №22 . Resolva a equação e indique a soma das raízes em sua resposta: №23 . Resolva a equação e indique o número de soluções em sua resposta:

Seção 8. Equações da forma │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

Para resolver equações deste tipo, é utilizado o método intervalar. Se resolvermos por expansão sequencial de módulos, obtemos n conjuntos de sistemas, o que é muito complicado e inconveniente. Consideremos o algoritmo do método de intervalo: 1). Encontre valores de variáveis X, para o qual cada módulo é igual a zero (zeros de expressões submodulares):
2). Marque os valores encontrados em uma reta numérica, que é dividida em intervalos (o número de intervalos é respectivamente igual a n+1 )3). Determine com que sinal cada módulo se revela em cada um dos intervalos obtidos (ao fazer uma solução, pode-se usar uma reta numérica, marcando os sinais nela) 4). A equação original é equivalente ao agregado n+1 sistemas, em cada um dos quais a associação da variável é indicada X um dos intervalos. Exemplos: №1 . Resolva a equação e indique a maior raiz em sua resposta:
1). Vamos encontrar os zeros das expressões submodulares: x = 2; x = -3 2). Vamos marcar os valores encontrados na reta numérica e determinar com qual sinal cada módulo é revelado nos intervalos resultantes:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- sem soluções A equação tem duas raízes. Resposta: a maior raiz x = 2. №2. Resolva a equação e forneça a raiz completa em sua resposta:
1). Vamos encontrar os zeros das expressões submodulares: x = 1,5; x = - 1 2). Vamos marcar os valores encontrados na reta numérica e determinar com qual sinal cada módulo é revelado nos intervalos resultantes: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
O último sistema não tem soluções, portanto a equação tem duas raízes. Ao resolver a equação, você deve prestar atenção ao sinal “-” na frente do segundo módulo. Resposta: raiz inteira x = 7. №3. Resolva a equação, indique a soma das raízes na sua resposta: 1). Vamos encontrar os zeros das expressões submodulares: x = 5; x = 1; x = - 2 2). Vamos marcar os valores encontrados na reta numérica e determinar com que sinal cada módulo é revelado nos intervalos resultantes: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
A equação tem duas raízes x = 0 e 2. Resposta: a soma das raízes é 2. №4 . Resolva a equação: 1). Vamos encontrar os zeros das expressões submodulares: x = 1; x = 2; x = 3.2). Vamos determinar com que sinal cada módulo é revelado nos intervalos resultantes. 3).
Vamos combinar as soluções dos três primeiros sistemas. Responder: ; x = 5.
Exercícios: №24. Resolva a equação:
№25. Resolva a equação e indique a soma das raízes em sua resposta: №26. Resolva a equação e indique a raiz menor em sua resposta: №27. Resolva a equação e indique a raiz maior em sua resposta:

Seção 9. Equações contendo vários módulos

Equações contendo múltiplos módulos assumem a presença de valores absolutos em expressões submodulares. O princípio básico para resolver equações deste tipo é a divulgação sequencial dos módulos, começando pelo “externo”. Durante a solução, são utilizadas as técnicas discutidas nas seções nº 1, nº 3.

Exemplos: №1. Resolva a equação:
Resposta: x = 1; - onze. №2. Resolva a equação:
Resposta: x = 0; 4; - 4. №3. Resolva a equação e indique o produto das raízes na sua resposta:
Resposta: o produto das raízes é – 8. №4. Resolva a equação:
Vamos denotar as equações da população (1) E (2) e considere a solução para cada um deles separadamente para facilitar o design. Como ambas as equações contêm mais de um módulo, é mais conveniente realizar uma transição equivalente para conjuntos de sistemas. (1)

(2)


Responder:
Exercícios: №36. Resolva a equação, indique a soma das raízes em sua resposta: 5 │3x-5│ = 25 x №37. Resolva a equação, se houver mais de uma raiz, indique a soma das raízes na sua resposta: │x + 2│ x – 3x – 10 = 1 №38. Resolva a equação: 3 │2х -4│ = 9 │х│ №39. Resolva a equação, em sua resposta indique o número de raízes por: 2 │ sen x│ = √2 №40 . Resolva a equação e indique o número de raízes em sua resposta:

Seção 3. Equações logarítmicas.

Antes de resolver as equações a seguir, é necessário revisar as propriedades dos logaritmos e da função logarítmica. Exemplos: №1. Resolva a equação, indique o produto das raízes em sua resposta: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Caso 1: se x ≥ - 1, então log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – satisfaz a condição x ≥ - 1 2 caso: se x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – satisfaz a condição x - 1
Resposta: o produto das raízes é – 15.
№2. Resolva a equação, indique a soma das raízes em sua resposta: lg
O.D.Z.

Resposta: a soma das raízes é 0,5.
№3. Resolva a equação: log 5
O.D.Z.

Resposta: x = 9. №4. Resolva a equação: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Vamos usar a fórmula para passar para outra base. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Vamos encontrar os zeros das expressões submodulares: x = 25; x = Esses números dividem a faixa de valores aceitáveis ​​em três intervalos, portanto a equação equivale a um conjunto de três sistemas.
Responder: )