Oscillations du système prédateur-proie (modèle Lotka-Voltaire). Cours : Recherche qualitative du modèle prédateur-proie Modèle mathématique du système proie-prédateur
Modèles d'interaction de deux types
Les hypothèses de Volterra. Analogies avec la cinétique chimique. Modèles d'interactions Volterra. Classification des types d'interactions Concurrence. Chasseur chassé. Modèles généralisés d'interactions d'espèces . Modèle Kolmogorov. Modèle de MacArthur d'interaction entre deux espèces d'insectes. Paramétrique et des portraits de phase du système Bazykin.
Le fondateur de la théorie mathématique moderne des populations est à juste titre considéré comme le mathématicien italien Vito Volterra, qui a développé la théorie mathématique des communautés biologiques, dont l'appareil est constitué d'équations différentielles et intégro-différentielles.(Vito Volterra. Lecons sur la Théorie Mathématique de la Lutte pour la Vie. Paris, 1931). Au cours des décennies suivantes, la dynamique démographique s’est développée principalement conformément aux idées exprimées dans ce livre. La traduction russe du livre de Volterra a été publiée en 1976 sous le titre : « La théorie mathématique de la lutte pour l'existence » avec une postface de Yu.M. Svirezhev, qui examine l'histoire du développement de l'écologie mathématique au cours de la période 1931-1976.
Le livre de Volterra est écrit de la même manière que les livres sur les mathématiques. Il formule d’abord quelques hypothèses sur les objets mathématiques censés être étudiés, puis mène une étude mathématique des propriétés de ces objets.
Les systèmes étudiés par Volterra se composent de deux ou plusieurs types. Dans certains cas, la fourniture de nourriture utilisée est prise en compte. Les équations décrivant l'interaction de ces types sont basées sur les concepts suivants.
Les hypothèses de Volterra
1. La nourriture est soit disponible en quantité illimitée, soit son approvisionnement est strictement réglementé dans le temps.
2. Les individus de chaque espèce meurent de telle manière qu'une proportion constante d'individus existants meurt par unité de temps.
3. Les espèces prédatrices mangent des victimes, et par unité de temps le nombre de victimes mangées est toujours proportionnel à la probabilité de rencontrer des individus de ces deux espèces, c'est-à-dire le produit du nombre de prédateurs et du nombre de proies.
4. S'il existe de la nourriture en quantité limitée et plusieurs espèces capables de la consommer, alors la part de nourriture consommée par une espèce par unité de temps est proportionnelle au nombre d'individus de cette espèce, pris avec un certain coefficient en fonction de la espèces (modèles de compétition interspécifique).
5. Si une espèce se nourrit de nourriture disponible en quantités illimitées, l'augmentation du nombre d'espèces par unité de temps est proportionnelle au nombre d'espèces.
6. Si une espèce se nourrit de nourriture disponible en quantités limitées, alors sa reproduction est régulée par le taux de consommation alimentaire, c'est-à-dire par unité de temps, l’augmentation est proportionnelle à la quantité de nourriture consommée.
Analogies avec la cinétique chimique
Ces hypothèses ont des parallèles étroits avec la cinétique chimique. Dans les équations de la dynamique des populations, comme dans les équations de la cinétique chimique, le « principe de collision » est utilisé, lorsque la vitesse de réaction est proportionnelle au produit des concentrations des composants en réaction.
En effet, selon les hypothèses de Volterra, la vitesse processus L'extinction de chaque espèce est proportionnelle au nombre d'espèces. En cinétique chimique, cela correspond à une réaction monomoléculaire de décomposition d'une certaine substance, et dans un modèle mathématique, cela correspond à des termes linéaires négatifs sur les côtés droits des équations.
Selon les concepts de cinétique chimique, la vitesse de la réaction bimoléculaire d'interaction entre deux substances est proportionnelle à la probabilité de collision de ces substances, c'est-à-dire le produit de leur concentration. De la même manière, conformément aux hypothèses de Volterra, le taux de reproduction des prédateurs (mort des proies) est proportionnel à la probabilité de rencontres entre individus prédateurs et proies, c'est-à-dire le produit de leurs nombres. Dans les deux cas, les termes bilinéaires apparaissent dans le système modèle à droite des équations correspondantes.
Enfin, les termes positifs linéaires du membre de droite des équations de Volterra, correspondant à la croissance des populations dans des conditions illimitées, correspondent aux termes autocatalytiques réactions chimiques. Cette similitude des équations dans les modèles chimiques et environnementaux permet d'appliquer les mêmes méthodes de recherche pour la modélisation mathématique de la cinétique des populations que pour les systèmes de réactions chimiques.
Classification des types d'interactions
Conformément aux hypothèses de Volterra, l'interaction de deux espèces dont le nombre X 1 et X 2 peut être décrit par les équations :
(9.1)
Voici les paramètres un je - des constantes du taux de croissance propre à l'espèce, c je- constantes d'autolimitation des nombres (compétition intraspécifique), b je- les constantes d'interaction des espèces, (je, j= 1,2). Les signes de ces coefficients déterminent le type d'interaction.
Dans la littérature biologique, les interactions sont généralement classées selon les mécanismes impliqués. La diversité est ici énorme : interactions trophiques diverses, interactions chimiques existant entre bactéries et algues planctoniques, interactions de champignons avec d'autres organismes, succession d'organismes végétaux, associées notamment à la compétition pour lumière du soleil et avec l'évolution des sols, etc. Cette classification semble vaste.
E . Odum, prenant en compte les modèles proposés par V. Volterra, a proposé une classification non par mécanismes, mais par résultats. Selon cette classification, les relations doivent être évaluées comme positives, négatives ou neutres selon que l'abondance d'une espèce augmente, diminue ou reste inchangée en présence d'une autre espèce. Ensuite, les principaux types d’interactions peuvent être présentés sous forme de tableau.
TYPES D'INTERACTIONS D'ESPÈCES
|
SYMBIOSE |
b 12 ,b 21 >0 |
||
|
COMMENSALISME |
b 12 ,>0, b 21 =0 |
||
|
PRÉDATEUR-VICTIME |
b 12 ,>0, b 21 <0 |
||
|
AMENSALISME |
b 12 ,=0, b 21 <0 |
||
|
CONCOURS |
b 12 , b 21 <0 |
||
|
NEUTRALISME |
b 12 , b 21 =0 |
La dernière colonne montre les signes des coefficients d'interaction du système (9.1)
Regardons les principaux types d'interactions
ÉQUATIONS DE CONCURRENCE :
Comme nous l'avons vu dans la leçon 6, les équations de compétition sont :
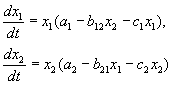 (9.2)
(9.2)
Solutions de systèmes stationnaires :
(1).
![]()
L'origine des coordonnées, pour tout paramètre du système, est un nœud instable.
(2).
![]() (9.3)
(9.3)
C l’état stationnaire (9.3) est une selle à un 1 >b 12 /Avec 2 et
nœud stable à un 1 12 /s 2 . Cette condition signifie qu’une espèce disparaît si son propre taux de croissance est inférieur à une certaine valeur critique.
(3).
![]() (9.4)
(9.4)
C solution stationnaire (9.4)¾ selle à un 2 >b 21 /c 1 et un nœud stable à un 2< b 21 /c 1
(4).
![]() (9.5)
(9.5)
L'état stationnaire (9.5) caractérise la coexistence de deux espèces concurrentes et représente un nœud stable si la relation est satisfaite :
![]()
Cela implique l'inégalité :
b 12
b 21
permettant de formuler la condition de coexistence des espèces :
Le produit des coefficients d'interaction inter-population est inférieur au produit des coefficients au sein de l'interaction de population.
En effet, supposons que les taux de croissance naturels des deux espèces considéréesun 1 ,un 2 sont identiques. La condition nécessaire à la stabilité sera alors
c 2 > b 12 ,c 1 >b 21 .
Ces inégalités montrent qu’une augmentation de la taille d’un concurrent freine davantage sa propre croissance que celle d’un autre concurrent. Si les effectifs des deux espèces sont limités, partiellement ou totalement, par des ressources différentes, les inégalités ci-dessus sont valables. Si les deux espèces ont exactement les mêmes besoins, alors l’une d’elles sera plus viable et supplantera son concurrent.
Le comportement des trajectoires de phase du système donne une idée claire des résultats possibles de la compétition. Égalisons les membres droits des équations du système (9.2) à zéro :
X 1 (un 1 –c 1 X 1 – b 12 X 2) = 0 (dx 1 /dt = 0),
X 2 (un 2 –b 21 X 1 – c 2 X 2) = 0 (dx 2 /dt = 0),
Dans ce cas, on obtient des équations pour les principales isoclines du système
X 2 = – b 21 X 1 / c 2 +un 2 /c 2, X 2 = 0
– équations des isoclines de tangentes verticales.
X 2 = – c 1 X 1 / b 12 + un 1 /b 12 , X 1 = 0
– équations des isoclines de tangentes verticales. Les points d'intersection par paires des isoclines des systèmes tangents verticaux et horizontaux représentent des solutions stationnaires du système d'équations (9.2.) et leurs coordonnées ![]() sont des nombres stationnaires d’espèces concurrentes.
sont des nombres stationnaires d’espèces concurrentes.
L'emplacement possible des principales isoclines dans le système (9.2) est illustré à la Fig. 9.1. Riz. 9.1UNcorrespond à la survie de l'espèceX 1, fig. 9.1 b– survie de l'espèceX 2, fig. 9.1 V– la coexistence des espèces lorsque la condition (9.6) est satisfaite. Graphique 9.1gdémontre le système de déclenchement. Ici, le résultat de la concurrence dépend des conditions initiales. L’état stationnaire non nul (9.5) pour les deux types est instable. C'est la selle par laquelle passe la séparatrice, séparant les zones de survie de chaque espèce.

Riz. 9.1.Localisation des principales isoclines sur le portrait de phase du système de compétition Volterra de deux types (9.2) avec des rapports de paramètres différents. Explications dans le texte.
Pour étudier la compétition entre espèces, des expériences ont été menées sur une grande variété d’organismes. En règle générale, deux espèces étroitement apparentées sont sélectionnées et cultivées ensemble et séparément dans des conditions strictement contrôlées. A certains intervalles, un recensement complet ou sélectif de la population est effectué. Les données de plusieurs expériences répétées sont enregistrées et analysées. Des études ont été menées sur des protozoaires (en particulier les ciliés), de nombreuses espèces de coléoptères du genre Tribolium, la drosophile et des crustacés d'eau douce (daphnies). De nombreuses expériences ont été réalisées sur des populations microbiennes (voir cours 11). Des expériences ont également été menées dans la nature, notamment sur des planaires (Reynolds), deux espèces de fourmis (Pontin), etc. 9.2. représente les courbes de croissance des diatomées utilisant la même ressource (occupant la même niche écologique). Lorsqu'il est cultivé en monoculture Astérionelle de Formose atteint un niveau de densité constant et maintient la concentration de la ressource (silicate) à un niveau constamment bas. B. Lorsqu'il est cultivé en monoculture Synédrauine se comporte de manière similaire et maintient la concentration en silicate à un niveau encore plus bas. B. Pendant la co-culture (en double exemplaire) Synedrauina déplace Asterionella formosa. Apparemment Synedra

Riz. 9.2.Compétition chez les diatomées. UN - lorsqu'il est cultivé en monoculture Astérionelle de Formose atteint un niveau de densité constant et maintient la concentration de la ressource (silicate) à un niveau constamment bas. b- lorsqu'il est cultivé en monoculture Synédrauine se comporte de manière similaire et maintient la concentration en silicate à un niveau encore plus bas. V- avec co-culture (en double exemplaire) Synedruina déplace Asterionella formosa. Apparemment Synedra remporte le concours grâce à sa capacité à utiliser plus pleinement le substrat (voir également la leçon 11).
Les expériences d'étude de la compétition de G. Gause sont largement connues, démontrant la survie d'une des espèces concurrentes et lui permettant de formuler la « loi d'exclusion compétitive ». La loi stipule qu’une seule espèce peut exister dans une niche écologique. En figue. 9.3. Les résultats des expériences de Gause sont présentés pour deux espèces de Parametium, occupant la même niche écologique (Fig. 9.3 a, b) et des espèces occupant des niches écologiques différentes (Fig. 9.3 c).

Riz. 9.3. UN- Courbes de croissance de la population de deux espèces Paramétium dans les cultures monospécifiques. Cercles noirs – P Aurelia, cercles blancs – P. Caudé
b- Courbes de croissance de P Aurelia et P . Caudé dans une culture mixte.
Par Gause, 1934
Le modèle de compétition (9.2) présente des inconvénients, en particulier, il s'ensuit que la coexistence de deux espèces n'est possible que si leur nombre est limité par des facteurs différents, mais le modèle n'indique pas quelle doit être l'ampleur des différences pour assurer une coexistence à long terme . Dans le même temps, on sait que pour une coexistence à long terme dans un environnement changeant, une différence atteignant une certaine ampleur est nécessaire. L'introduction d'éléments stochastiques dans le modèle (par exemple, l'introduction d'une fonction d'utilisation des ressources) nous permet d'étudier quantitativement ces questions.
Système PRÉDATEUR+VICTIME
 (9.7)
(9.7)
Ici, contrairement à (9.2), les signes b 12 Et b 21 sont différents. Comme dans le cas de la concurrence, l'origine
![]() (9.8)
(9.8)
est un point particulier du type nœud instable. Trois autres états stationnaires possibles :
![]() ,(9.9)
,(9.9)
![]() (9.10)
(9.10)
![]() (9.11)
(9.11)
Ainsi, seules les proies peuvent survivre (9.10), uniquement le prédateur (9.9) (s'il dispose d'autres sources de nourriture) et la coexistence des deux espèces (9.11). Nous avons déjà discuté de la dernière option dans la leçon 5. Les types possibles de portraits de phase pour un système prédateur-proie sont présentés dans la Fig. 9.4.
Les isoclines des tangentes horizontales sont des lignes droites
X 2 = – b 21 X 1 /c 2 + un 1/c 2, X 2 = 0,
et isoclines des tangentes verticales- droit
X 2 = – c 1 X 1 /b 12 + un 2 /b 12 , X 1 = 0.
Les points stationnaires se trouvent à l'intersection des isoclines tangentes verticales et horizontales.

De la fig. 9.4 ce qui suit est visible. Système prédateur-proie (9.7) peut avoir une position d’équilibre stable, dans laquelle o La population de victimes du rhum a complètement disparu ( ) et seuls les prédateurs sont restés (période 2 sur la fig. 9.4 UN). Évidemment, une telle situation ne peut se réaliser que si, outre le type de victimes en question, X 1 prédateur X 2 – dispose de sources d’alimentation supplémentaires. Ce fait est reflété dans le modèle par le terme positif du côté droit de l’équation pour x2. Points spéciaux(1) et (3) (Fig. 9.4 UN) sont instables. Deuxième possibilité – un état stationnaire stable dans lequel la population de prédateurs a complètement disparu et seules les proies restent – point stable(3) (Fig. 9.4 6 ). C'est un point particulier (1) – également un nœud instable.
Enfin, la troisième possibilité – coexistence durable des populations de prédateurs et de proies (Fig. 9.4 V), dont les nombres stationnaires sont exprimés par les formules (9.11).
Comme dans le cas d’une population (voir leçon 3), pour le modèle (9.7) Il est possible de développer un modèle stochastique, mais il ne peut être résolu explicitement. Nous nous limiterons donc à des considérations générales. Supposons par exemple que le point d'équilibre soit situé à une certaine distance de chacun des axes. Puis pour les trajectoires de phase sur lesquelles les valeursX 1 , X 2 restent suffisamment grands, un modèle déterministe sera tout à fait satisfaisant. Mais si à un moment donné de la trajectoire de la phase, une variable n’est pas très grande, alors les fluctuations aléatoires peuvent devenir significatives. Ils conduisent au fait que le point représentatif se déplace vers l'un des axes, ce qui entraîne l'extinction de l'espèce correspondante.
Ainsi, le modèle stochastique s'avère instable, puisque la « dérive » stochastique conduit tôt ou tard à l'extinction de l'une des espèces. Dans ce type de modèle, le prédateur finit par disparaître, soit par hasard, soit parce que sa population de proies est éliminée en premier. Le modèle stochastique du système prédateur-proie explique bien les expériences de Gause (Gause, 1934), dans lequel les ciliés Paramettum candatum servi de victime à un autre cilié Didinium nasatum – prédateur. Attendu selon les équations déterministes (9.7) les nombres d'équilibre dans ces expériences étaient d'environ cinq individus de chaque espèce, il n'est donc pas surprenant que dans chaque expérience répétée, soit les prédateurs, soit les proies (et après eux les prédateurs) disparaissent assez rapidement. En figue. 9.5.

Riz. 9.5. Hauteur Paramétium caudatum et ciliés prédateurs Dadinium nasutum. Depuis : Gause G.F. La lutte pour l'existence. Baltimore, 1934
Ainsi, l'analyse des modèles Volterra d'interaction entre les espèces montre que, malgré la grande variété de types de comportement de tels systèmes, il ne peut y avoir de fluctuations non amorties du nombre dans le modèle d'espèces concurrentes. Cependant, de telles oscillations sont observées dans la nature et expérimentalement. La nécessité de leur explication théorique était l'une des raisons pour lesquelles les descriptions de modèles étaient formulées sous une forme plus générale.
Modèles généralisés d'interaction de deux types
Un grand nombre de modèles ont été proposés pour décrire l'interaction des espèces, dont les membres droits des équations étaient fonction du nombre de populations en interaction. La question de l'élaboration de critères généraux pour établir quel type de fonctions peuvent décrire le comportement de la taille temporaire de la population, y compris les fluctuations stables, a été résolue. Les plus célèbres de ces modèles appartiennent à Kolmogorov (1935, article révisé - 1972) et Rosenzweig (1963).
 (9.12)
(9.12)
Le modèle comprend les hypothèses suivantes :
1) Les prédateurs n'interagissent pas entre eux, c'est-à-dire taux de reproduction des prédateurs k 2 et nombre de victimes L exterminé par unité de temps par un prédateur ne dépend pas de y.
2) L'augmentation du nombre de proies en présence de prédateurs est égale à l'augmentation en l'absence de prédateurs moins le nombre de proies exterminées par les prédateurs. Les fonctions k 1 (X), k 2 (X), L(X), sont continues et définies sur le demi-axe positif X, oui³ 0.
3) n'importe quoi 1 /dx< 0. Cela signifie que le taux de reproduction des proies en l'absence de prédateur diminue de façon monotone avec l'augmentation du nombre de proies, ce qui reflète la disponibilité limitée de nourriture et d'autres ressources.
4) n'importe quoi 2 /dx> 0, k 2 (0) < 0 < k 2 (¥ ). Avec une augmentation du nombre de proies, le coefficient de reproduction des prédateurs diminue de façon monotone avec une augmentation du nombre de proies, passant de valeurs négatives, (quand il n'y a rien à manger) au positif.
5) Le nombre de proies détruites par un prédateur par unité de temps L(X)> 0 à N> 0; L(0)=0.
Les types possibles de portraits de phase du système (9.12) sont présentés sur la Fig. 9.6 :

Riz. 9.6.Portraits de phase du système de Kolmogorov (9.12), qui décrit l'interaction de deux types à différents rapports de paramètres. Explications dans le texte.
Les solutions stationnaires (il y en a deux ou trois) ont les coordonnées suivantes :
(1). ` x=0 ;` y=0.
L'origine des coordonnées de toutes les valeurs de paramètres est une selle (Fig. 9.6 a-d).
(2). ` x=UNE,` y = 0.(9.13)
UNdéterminé à partir de l’équation :
k 1 (UN)=0.
Stationnaire la solution (9.13) est une selle si B< UN (Fig. 9.6 UN, b, g), B déterminé à partir de l'équation
k 2 (B)=0
Le point (9.13) est placé dans le quadrant positif si B>A . C'est un nœud stable .
Le dernier cas, qui correspond à la mort du prédateur et à la survie de la proie, est représenté sur la Fig. 9.6 V.
(3). ` x=B,` y=C.(9.14)
La valeur de C est déterminée à partir des équations :
Point (9.14) – mise au point (Fig.9.6 UN) ou nœud (Fig.9.6 g), dont la stabilité dépend du signe de la grandeurs
s 2 = – k 1 (B) –k 1 (B)B+L(B)C.
Si s>0, un point est stable sis<0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 b)
Dans la littérature étrangère, un modèle similaire proposé par Rosenzweig et MacArthur (1963) est plus souvent considéré :
 (9.15)
(9.15)
Où F(X) - taux de variation du nombre de victimes X en l'absence de prédateurs, F( x,y) - intensité de la prédation, k- coefficient caractérisant l'efficacité de transformation de la biomasse des proies en biomasse des prédateurs, e- mortalité des prédateurs.
Le modèle (9.15) se réduit à un cas particulier du modèle de Kolmogorov (9.12) sous les hypothèses suivantes :
1) le nombre de prédateurs n'est limité que par le nombre de proies,
2) la vitesse à laquelle un prédateur donné mange sa proie dépend uniquement de la densité de la population de proies et ne dépend pas de la densité de la population de prédateurs.
Alors les équations (9.15) prennent la forme.

Lors de la description de l'interaction d'espèces réelles, les membres droits des équations sont spécifiés conformément aux idées sur les réalités biologiques. Considérons l'un des modèles les plus populaires de ce type.
Modèle d'interaction entre deux types d'insectes (MacArthur, 1971)
Le modèle, que nous examinerons ci-dessous, a été utilisé pour résoudre le problème pratique du contrôle des insectes nuisibles en stérilisant les mâles d'une des espèces. Sur la base des caractéristiques biologiques de l'interaction des espèces, le modèle suivant a été écrit
 (9.16)
(9.16)
Ici x,y- biomasse de deux types d'insectes. Les interactions trophiques des espèces décrites dans ce modèle sont très complexes. Cela détermine la forme des polynômes sur les membres droits des équations.
Regardons le côté droit de la première équation. Espèces d'insectes X manger les larves de l'espèce à(membre +k 3 y), mais les adultes de l'espèce à manger les larves de l'espèce X soumis à une forte abondance d’espèces X ou à ou les deux types (membres –k 4 xy, – y2). Au petit X mortalité des espèces X supérieur à son accroissement naturel (1 –k 1 +k 2 x-x 2 < 0 au petit X). Dans la deuxième équation, le terme k 5 reflète la croissance naturelle de l’espèce oui ; –k 6 oui – une telle maîtrise de soi,–k 7 X– manger des larves de l’espèce à espèces d'insectes x,k 8 xy – augmentation de la biomasse des espèces à en raison de la consommation par les insectes adultes de l'espèce à larves de l'espèce X.
En figue. 9.7 un cycle limite est présenté, qui est la trajectoire d'une solution périodique stable du système (9.16).

La solution à la question de savoir comment assurer la coexistence d'une population avec son environnement biologique ne peut bien entendu être obtenue sans prendre en compte les spécificités d'un système biologique particulier et sans analyser toutes ses interrelations. Parallèlement, l'étude de modèles mathématiques formels permet de répondre à quelques questions générales. On peut affirmer que pour des modèles comme (9.12), le fait de compatibilité ou d'incompatibilité des populations ne dépend pas de leur taille initiale, mais est déterminé uniquement par la nature de l'interaction des espèces. Le modèle permet de répondre à la question : comment influencer la biocénose et la gérer afin de détruire rapidement les espèces nuisibles.
La gestion peut être réduite à un changement brusque et à court terme des valeurs de la population X Et toi. Cette méthode correspond à des méthodes de contrôle telles que la destruction ponctuelle d'une ou des deux populations par des moyens chimiques. Il ressort clairement de la déclaration formulée ci-dessus que, pour des populations compatibles, cette méthode de contrôle sera inefficace, car avec le temps, le système atteindra à nouveau un régime stationnaire.
Une autre façon consiste à modifier le type de fonctions d'interaction entre les vues, par exemple lors de la modification des valeurs des paramètres système. C'est à cette méthode paramétrique que correspondent les méthodes de lutte biologique. Ainsi, lorsque des mâles stérilisés sont introduits, le taux de croissance naturelle de la population diminue. Si en même temps nous obtenons un type différent de portrait de phase, où il n’y a qu’un état stationnaire stable avec un nombre nul de parasites, le contrôle conduira au résultat souhaité. – destruction de la population d'une espèce nuisible. Il est intéressant de noter qu'il est parfois conseillé d'appliquer l'impact non pas sur l'organisme nuisible lui-même, mais sur son partenaire. En général, il est impossible de dire quelle méthode est la plus efficace. Cela dépend des contrôles disponibles et de la forme explicite des fonctions décrivant l'interaction des populations.
Modèle par A.D. Bazykin
L'analyse théorique des modèles d'interactions d'espèces a été réalisée de manière plus complète dans le livre d'A.D. Bazykin « Biophysics of Interacting Populations » (M., Nauka, 1985).
Considérons l'un des modèles prédateur-proie étudiés dans cet ouvrage.
 (9.17)
(9.17)
Le système (9.17) est une généralisation du modèle prédateur-proie de Volterra le plus simple (5.17) prenant en compte l'effet de la saturation des prédateurs. Le modèle (5.17) suppose que l’intensité du pâturage des proies augmente linéairement avec l’augmentation de la densité des proies, ce qui ne correspond pas à la réalité à des densités de proies élevées. Différentes fonctions peuvent être choisies pour décrire la dépendance du régime alimentaire d'un prédateur à la densité de ses proies. Il est très important que le modèle choisi fonctionne avec la croissance X tend asymptotiquement vers une valeur constante. Le modèle (9.6) utilisait une dépendance logistique. Dans le modèle de Bazykin, l’hyperbole est choisie comme telle fonction X/(1+px). Rappelons qu'il s'agit de la forme de la formule Monod, qui décrit la dépendance du taux de croissance des micro-organismes sur la concentration du substrat. Ici, la proie joue le rôle de substrat et le prédateur joue le rôle de micro-organismes. .
Le système (9.17) dépend de sept paramètres. Le nombre de paramètres peut être réduit en remplaçant les variables :
X® (ANNONCE)X; oui ® (ANNONCE)/y;
t® (1/A)t ; g (9.18)
et dépend de quatre paramètres.
Pour une étude qualitative complète, il est nécessaire de diviser l'espace des paramètres à quatre dimensions en zones présentant différents types de comportement dynamique, c'est-à-dire construire un portrait paramétrique ou structurel du système.
Il faut ensuite construire des portraits de phase pour chacune des zones du portrait paramétrique et décrire les bifurcations qui se produisent avec les portraits de phase aux limites des différentes zones du portrait paramétrique.
La construction d'un portrait paramétrique complet s'effectue sous la forme d'un ensemble de « tranches » (projections) d'un portrait paramétrique de basse dimension avec des valeurs fixes de certains des paramètres.
Portrait paramétrique du système (9.18) pour fixe g et petit e présenté sur la figure 9.8. Le portrait contient 10 zones avec différents types de comportement des trajectoires de phase.

Riz. 9.8.Portrait paramétrique du système (9.18) pour fixeg
et petit e
Le comportement du système à différents rapports de paramètres peut être significativement différent (Fig. 9.9). Le système permet :
1) un équilibre stable (régions 1 et 5) ;
2) un cycle limite stable (régions 3 et 8) ;
3) deux équilibres stables (région 2)
4) cycle limite stable et équilibre instable à l'intérieur (régions 6, 7, 9, 10)
5) cycle limite stable et équilibre stable en dehors de celui-ci (région 4).
Dans les régions paramétriques 7, 9, 10, la région d'attraction d'équilibre est limitée par un cycle limite instable situé à l'intérieur d'un cycle stable. La structure la plus intéressante est le portrait de phase, correspondant à la zone 6 du portrait paramétrique. Il est montré en détail sur la Fig. 9.10.

La zone d'attraction de l'équilibre B 2 (ombrée) est un « escargot » se tordant à partir du foyer instable B 1. Si l'on sait qu'à l'instant initial le système était au voisinage de B 1, alors il est possible de juger si la trajectoire correspondante atteindra l'équilibre B 2 ou un cycle limite stable entourant trois points d'équilibre C (selle), B 1 et B 2 basés sur des considérations probabilistes.

Figure 9.10.Portrait de phase du système 9.18 pour la région paramétrique 6. La région d'attraction B 2 est ombrée
Dans un portrait paramétrique(9.7) il y a 22 diverses limites de bifurcation qui forment 7 divers types de bifurcations. Leur étude permet d'identifier les types possibles de comportement du système lorsque ses paramètres changent. Par exemple, lorsque vous quittez la zone 1 à la zone 3 la naissance d'un petit cycle limite se produit, ou la naissance douce d'auto-oscillations autour d'un équilibre unique DANS. Une naissance en douceur similaire d'auto-oscillations, mais autour d'un des équilibres, à savoir B 1 , se produit lors du franchissement des frontières des régions 2 et 4. En quittant la zone 4 à la zone 5 cycle limite stable autour d'un pointB 1 « éclate » sur la boucle des séparatrices et le seul point attractif reste l'équilibre B 2 etc.
Bien entendu, le développement de critères de proximité d’un système par rapport aux limites de bifurcation est particulièrement intéressant pour la pratique. En effet, les biologistes sont bien conscients de la propriété « tampon » ou de « flexibilité » des systèmes écologiques naturels. Ces termes font généralement référence à la capacité d’un système à absorber les influences extérieures. Tant que l’intensité de l’influence externe ne dépasse pas une certaine valeur critique, le comportement du système ne subit pas de changements qualitatifs. Sur le plan des phases, cela correspond au retour du système à un état d'équilibre stable ou à un cycle limite stable dont les paramètres ne diffèrent pas beaucoup de celui d'origine. Lorsque l'intensité de l'impact dépasse le niveau admissible, le système « tombe en panne » et passe à un mode de comportement dynamique qualitativement différent, par exemple, il s'éteint tout simplement. Ce phénomène correspond à une transition de bifurcation.
Chaque type de transition de bifurcation a ses particularités, qui permettent de juger du danger d'une telle transition pour l'écosystème. Voici quelques critères généraux indiquant la proximité d’une frontière dangereuse. Comme dans le cas d'une espèce, si, lorsque le nombre d'une des espèces diminue, le système « reste bloqué » près d'un point selle instable, ce qui se traduit par une restauration très lente du nombre à la valeur initiale, alors le Le système est proche de la limite critique. Un indicateur de danger est également un changement dans la forme des fluctuations du nombre de prédateurs et de proies. Si des oscillations proches de l'harmonique deviennent des oscillations de relaxation et que l'amplitude des oscillations augmente, cela peut entraîner une perte de stabilité du système et l'extinction d'une des espèces.
L'approfondissement de la théorie mathématique des interactions entre espèces va dans le sens de détailler la structure des populations elles-mêmes et de prendre en compte des facteurs temporels et spatiaux.
Littérature.
Kolmogorov A.N. Etude qualitative de modèles mathématiques de dynamique des populations. // Problèmes de cybernétique. M., 1972, numéro 5.
MacArtur R. Analyse graphique des systèmes écologiques // Rapport de la Division de biologie de l'Université Perinceton. 1971
A.D. Bazykin « Biophysique des populations en interaction ». M., Nauka, 1985.
V. Volterra : « Théorie mathématique de la lutte pour l'existence ». M.. Sciences, 1976
Gause G.F. La lutte pour l'existence. Baltimore, 1934.
MODÈLE INFORMATIQUE « PRÉDATEUR-VICTIME »
Kazachkov Igor Alekseevich 1, Guseva Elena Nikolaevna 2
1 Université technique d'État de Magnitogorsk. G.I. Nosova, Institut de Construction, Architecture et Art, étudiante en 5ème année
2 Université technique d'État de Magnitogorsk. G.I. Nosova, Institut de l'énergie et des systèmes automatisés, candidat en sciences pédagogiques, professeur agrégé du Département d'informatique de gestion et technologies de l'information
annotation
Cet article est consacré à un aperçu du modèle informatique « prédateur-proie ». Les recherches menées suggèrent que la modélisation environnementale joue un rôle énorme dans la recherche environnementale. Cette question est multiforme.
MODÈLE INFORMATIQUE "PRÉDATEUR-VICTIME"
Kazatchkov Igor Alekseevich 1, Guseva Elena Nikolaevna 2
1 Université technique d'État de Nosov Magnitogorsk, Institut de génie civil, d'architecture et d'art, étudiant du 5ème cours
2 Université technique d'État de Nosov Magnitogorsk, Institut d'ingénierie énergétique et de systèmes automatisés, docteur en sciences pédagogiques, professeur agrégé du département d'informatique commerciale et de technologies de l'information
Abstrait
Cet article donne un aperçu du modèle informatique « prédateur-victime ». L'étude suggère que la simulation environnementale joue un rôle important dans l'étude de l'environnement. Ce problème est multiforme.
La modélisation écologique est utilisée pour étudier notre environnement. Les modèles mathématiques sont utilisés dans les cas où il n'y a pas d'environnement naturel ni d'objets naturels ; ils permettent de prédire l'influence de divers facteurs sur l'objet étudié. Cette méthode assume les fonctions de vérification, de construction et d'interprétation des résultats obtenus. Sur la base de telles formes, la modélisation environnementale traite de l'évaluation des changements dans l'environnement qui nous entoure.
Actuellement, de telles formes sont utilisées pour étudier l'environnement qui nous entoure, et lorsqu'il est nécessaire d'étudier l'un de ses domaines, une modélisation mathématique est utilisée. Ce modèle permet de prédire l'influence de certains facteurs sur l'objet d'étude. À une certaine époque, le type « prédateur-proie » a été proposé par des scientifiques tels que : T. Malthus (Malthus 1798, Malthus 1905), Verhulst (Verhulst 1838), Pearl (Pearl 1927, 1930), ainsi que A. Lotka ( Lotka 1925, 1927) et V. Volterra (Volterra 1926). Ces modèles reproduisent le régime oscillatoire périodique qui résulte des interactions interspécifiques dans la nature.
L'une des principales méthodes de cognition est la modélisation. Outre le fait qu'il peut prédire les changements qui se produiront dans environnement, aide également à trouver la manière optimale de résoudre le problème. Les modèles mathématiques sont utilisés depuis longtemps en écologie afin d'établir des modèles et des tendances dans le développement des populations et de contribuer à mettre en évidence l'essence des observations. La mise en page peut servir d'exemple comportement, objet.
Lors de la recréation d'objets en biologie mathématique, des prévisions de divers systèmes sont utilisées, des individualités particulières des biosystèmes sont prévues : la structure interne de l'individu, les conditions de survie, la constance des systèmes écologiques, grâce à laquelle l'activité vitale des systèmes est préservée .
L’avènement de la modélisation informatique a considérablement repoussé les limites des capacités de recherche. La possibilité d'une mise en œuvre multilatérale de formes difficiles qui ne permettent pas une étude analytique est apparue ; de nouvelles orientations sont apparues, ainsi que la modélisation par simulation.
Considérons ce qu'est un objet de modélisation. « L’objet est un habitat fermé où se produit l’interaction entre deux populations biologiques : prédateurs et proies. Le processus de croissance, d'extinction et de reproduction se produit directement à la surface de l'habitat. La proie se nourrit des ressources présentes dans l'environnement, tandis que les prédateurs se nourrissent des proies. Dans ce cas, les ressources nutritionnelles peuvent être soit renouvelables, soit non renouvelables.
En 1931, Vito Volterra a dérivé les lois suivantes sur la relation prédateur-proie.
La loi du cycle périodique - le processus de destruction des proies par un prédateur conduit souvent à des fluctuations périodiques de la taille de la population des deux espèces, en fonction uniquement du taux de croissance des carnivores et des herbivores et du rapport initial de leur nombre.
Loi de conservation des moyennes - L'abondance moyenne de chaque espèce est constante, quel que soit le niveau initial, à condition que les taux spécifiques d'augmentation de la population, ainsi que l'efficacité de la prédation, soient constants.
La loi de la violation des valeurs moyennes - lorsque les deux espèces diminuent proportionnellement à leur nombre, la taille moyenne de la population des proies augmente et celle des prédateurs diminue.
Le modèle prédateur-proie est une relation particulière entre un prédateur et sa proie, dont tous deux bénéficient. Les individus les plus sains et les plus adaptés aux conditions environnementales survivent, c'est-à-dire tout cela se produit grâce à la sélection naturelle. Dans un environnement où il n'y a aucune possibilité de reproduction, le prédateur détruira tôt ou tard la population de la proie, ce qui entraînera son extinction.
Il existe de nombreux organismes vivants sur Terre qui, dans des conditions favorables, augmentent le nombre de leurs proches dans des proportions énormes. Cette capacité s'appelle : le potentiel biotique d'une espèce, c'est-à-dire une augmentation du nombre d'une espèce sur une certaine période de temps. Chaque espèce a son propre potentiel biotique, par exemple, les grandes espèces d'organismes ne peuvent augmenter que de 1,1 fois par an, tandis que les organismes d'espèces plus petites, comme les crustacés, etc. peuvent augmenter leur apparition jusqu'à 1030 fois, et les bactéries en nombre encore plus grand. Dans tous ces cas, la population augmentera de façon exponentielle.
La croissance démographique exponentielle est une progression géométrique de la croissance démographique. Cette capacité peut être observée en laboratoire chez les bactéries et les levures. Dans des conditions hors laboratoire, une croissance exponentielle peut être observée dans l’exemple des criquets ou d’autres types d’insectes. Une telle augmentation du nombre d'espèces peut être observée dans les endroits où il n'a pratiquement pas d'ennemis et où il y a plus qu'assez de nourriture. Finalement, une augmentation du nombre d'espèces, après que les effectifs aient augmenté pendant une courte période, la croissance de la population a commencé à décliner.
Considérons un modèle informatique de reproduction des mammifères en utilisant comme exemple le modèle Lotka-Volterra. Laisser Dans une certaine zone, deux types d'animaux vivent : les cerfs et les loups. Modèle mathématique des changements de population dans le modèle Plateaux-Volterra :
Le nombre initial de victimes est xn, le nombre de prédateurs est yn.
Paramètres du modèle :
P1 – probabilité de rencontrer un prédateur,
P2 – coefficient de croissance des prédateurs aux dépens des proies,
d – taux de mortalité des prédateurs,
a – coefficient d'augmentation du nombre de victimes.
Dans la tâche d'entraînement, les valeurs suivantes ont été fixées : le nombre de cerfs était de 500, le nombre de loups était de 10, le taux de croissance des cerfs était de 0,02, le taux de croissance des loups était de 0,1, la probabilité de rencontrer un prédateur était 0,0026, le taux de croissance des prédateurs aux dépens des proies était de 0,000056. Les données sont calculées pour 203 ans.
Nous explorons l'influence le coefficient d'augmentation des victimes pour le développement de deux populations, les paramètres restants resteront inchangés. Dans le schéma 1, on observe une augmentation du nombre de proies puis, avec un certain retard, une augmentation du nombre de prédateurs. Ensuite, les prédateurs assomment les victimes, le nombre de victimes diminue fortement et, par la suite, le nombre de prédateurs diminue (Fig. 1).

Figure 1. Taille de la population avec de faibles taux de natalité parmi les victimes
Analysons le changement de modèle en augmentant le taux de natalité de la victime a=0,06. Dans le diagramme 2, nous voyons un processus oscillatoire cyclique conduisant à une augmentation des effectifs des deux populations au fil du temps (Fig. 2).

Figure 2. Taille de la population au taux de natalité moyen des victimes
Considérons comment la dynamique de la population va changer avec une valeur élevée du taux de natalité de la victime a=1,13. En figue. 3, on observe une forte augmentation du nombre des deux populations, suivie par l'extinction des proies et des prédateurs. Cela est dû au fait que la population de proies a augmenté à un point tel que les ressources ont commencé à s'épuiser, entraînant l'extinction des proies. L'extinction des prédateurs est due au fait que le nombre de proies a diminué et que les prédateurs ont manqué de ressources pour survivre.

Figure 3. Taille de la population avec des taux de natalité élevés parmi les victimes
Sur la base de l'analyse des données d'expériences informatiques, nous pouvons conclure que la modélisation informatique nous permet de prédire la taille des populations et d'étudier l'influence de divers facteurs sur la dynamique des populations. Dans l'exemple ci-dessus, nous avons examiné le modèle prédateur-proie, l'influence du taux de natalité des proies sur le nombre de cerfs et de loups. Une légère augmentation de la population de proies entraîne une légère augmentation du nombre de proies qui, après un certain temps, sont détruites par les prédateurs. Une augmentation modérée de la population de proies entraîne une augmentation de la taille des deux populations. Une forte augmentation de la population de proies entraîne d'abord une augmentation rapide de la population de proies, ce qui affecte l'augmentation de la croissance des prédateurs, mais les prédateurs multipliés détruisent ensuite rapidement la population de cerfs. En conséquence, les deux espèces disparaissent.
Les prédateurs peuvent manger des herbivores ainsi que des prédateurs faibles. Les prédateurs disposent d’une large gamme de nourriture et passent facilement d’une proie à une autre, plus accessible. Les prédateurs attaquent souvent des proies faibles. L'équilibre écologique est maintenu entre les populations proies-prédateurs.[...]
Si l'équilibre est instable (il n'y a pas de cycles limites) ou si le cycle externe est instable, alors les nombres des deux espèces, connaissant de fortes fluctuations, quittent le voisinage de l'équilibre. De plus, une dégénérescence rapide (dans la première situation) se produit avec une faible adaptation du prédateur, c'est-à-dire avec sa mortalité élevée (par rapport au taux de reproduction de la victime). Cela signifie qu'un prédateur faible à tous égards ne contribue pas à la stabilisation du système et s'éteint lui-même.[...]
La pression des prédateurs est particulièrement forte lorsque, dans la coévolution prédateur-proie, l'équilibre se déplace vers le prédateur et l'aire de répartition des proies se rétrécit. La lutte compétitive est étroitement liée au manque de ressources alimentaires ; elle peut aussi être une lutte directe, par exemple, de prédateurs pour l'espace comme ressource, mais le plus souvent il s'agit simplement du déplacement d'une espèce qui n'a pas assez de nourriture dans un territoire donné par une espèce qui a suffisamment de la même quantité de nourriture. C'est déjà une compétition interspécifique.[...]
 |
Et enfin, dans le système « prédateur-proie » décrit par le modèle (2.7), l'émergence d'une instabilité de diffusion (avec stabilité de l'équilibre local) n'est possible que dans le cas où la mortalité naturelle du prédateur augmente avec la croissance de sa population plus vite que la mortalité naturelle du prédateur. la fonction linéaire et la fonction trophique diffèrent de Volterra ou lorsque la population de proies est une population de type Ollie.[...]
Théoriquement, dans les modèles « un prédateur - deux proies », un pâturage équivalent (manque de préférence pour l'une ou l'autre espèce de proie) peut affecter la coexistence compétitive des espèces de proies uniquement dans les endroits où un équilibre potentiellement stable existe déjà. La diversité ne peut augmenter que dans des conditions où les espèces moins compétitives ont un taux de croissance démographique plus élevé que les espèces dominantes. Cela nous permet de comprendre la situation où le pâturage uniforme conduit à une augmentation de la diversité des espèces végétales où un plus grand nombre d'espèces sélectionnées pour une reproduction rapide coexistent avec des espèces dont l'évolution vise à accroître la compétitivité.[...]
De même, la sélection des proies en fonction de la densité peut conduire à un équilibre stable dans les modèles théoriques de deux espèces de proies concurrentes là où aucun équilibre n'existait auparavant. Pour ce faire, le prédateur devrait être capable de réagir fonctionnellement et numériquement aux changements de densité des proies ; il est possible, cependant, que le changement (attaques disproportionnellement fréquentes contre les proies les plus abondantes) soit plus important. En fait, il a été établi que le changement a un effet stabilisant dans les systèmes « un prédateur – n proies » et représente le seul mécanisme capable de stabiliser les interactions dans les cas où les niches des proies se chevauchent complètement. Des prédateurs non spécialisés peuvent jouer un tel rôle. La préférence de prédateurs plus spécialisés pour un concurrent dominant agit de la même manière qu'un changement de prédateur et peut stabiliser les interactions théoriques dans des modèles dans lesquels il n'y avait auparavant aucun équilibre entre les espèces de proies, à condition que leurs niches soient dans une certaine mesure séparées.
De plus, un prédateur « fort à tous égards » ne stabilise pas la communauté, c'est-à-dire bien adapté à une proie donnée et avec une faible mortalité relative. Dans ce cas, le système a un cycle limite instable et, malgré la stabilité de la position d'équilibre, dégénère dans un environnement aléatoire (le prédateur mange la proie et meurt par conséquent). Cette situation correspond à une lente dégénérescence.[...]
Ainsi, avec une bonne adaptation d'un prédateur au voisinage d'un équilibre stable, des cycles instables et stables peuvent survenir, c'est-à-dire selon les conditions initiales, le système « prédateur-proie » soit tend à s'équilibrer, soit, oscillant, s'en éloigne, soit des fluctuations stables des effectifs des deux espèces s'établissent au voisinage de l'équilibre.
Les organismes classés comme prédateurs se nourrissent d'autres organismes, détruisant ainsi leurs proies. Ainsi, parmi les organismes vivants, il convient de distinguer un autre système de classification, à savoir « prédateurs » et « proies ». Les relations entre ces organismes se sont développées tout au long de l’évolution de la vie sur notre planète. Les organismes prédateurs agissent comme des régulateurs naturels du nombre de proies. Une augmentation du nombre de « prédateurs » entraîne une diminution du nombre de « proies », ce qui, à son tour, réduit l'approvisionnement en nourriture (« proies ») pour les « prédateurs », ce qui dicte généralement une diminution du nombre. de « proies », etc. Ainsi, dans la biocénose, des fluctuations du nombre de prédateurs et de proies se produisent constamment, mais en général, un certain équilibre s'établit pendant un certain temps dans des conditions environnementales assez stables.[... ]
Cela aboutit finalement à un équilibre écologique entre les populations de prédateurs et de proies.[...]
Pour une fonction trophique du troisième type, l'état d'équilibre sera stable si où N est le point d'inflexion de la fonction (voir Fig. 2, c). Cela découle du fait qu'au cours de l'intervalle, la fonction trophique est concave et, par conséquent, la part relative de la consommation de proies par le prédateur augmente.[...]
Soit Гг = -Г, c'est-à-dire il existe une communauté de type « prédateur-proie ». Dans ce cas, le premier terme de l'expression (7.4) est égal à zéro, et pour satisfaire la condition de stabilité en termes de probabilité de l'état d'équilibre N, il faut que le deuxième terme ne soit pas non plus positif.[.. .]
Ainsi, pour la communauté prédateur-proie considérée, nous pouvons conclure que la position d’équilibre positive globale est asymptotiquement stable, c’est-à-dire que pour toute donnée initiale 1H(0)>0, l’évolution se produit de telle manière que N(7) - ■ K à condition que N >0.[...]
Ainsi, dans un environnement homogène dépourvu d'abri pour la reproduction, le prédateur détruit tôt ou tard la population de proies puis s'éteint lui-même. Les vagues de vie » (changements dans l’abondance des prédateurs et des proies) se succèdent avec un déphasage constant, et en moyenne l’abondance des prédateurs et des proies reste approximativement au même niveau. La durée de la période dépend des taux de croissance des deux espèces et des paramètres initiaux. Pour la population de proies, l’influence du prédateur est positive, puisque sa reproduction excessive entraînerait un effondrement de sa population. À leur tour, tous les mécanismes qui empêchent l’extermination complète des proies contribuent à la préservation de l’approvisionnement alimentaire du prédateur.[...]
D'autres modifications peuvent être une conséquence du comportement du prédateur. Le nombre de proies qu'un prédateur est capable de consommer en temps donné, a sa limite. L'effet de la saturation des prédateurs à l'approche de ce seuil est présenté dans le tableau. 2-4, B. Les interactions décrites par les équations 5 et 6 peuvent avoir des points d'équilibre stables ou présenter des fluctuations cycliques. Cependant, de tels cycles sont différents de ceux reflétés dans les équations 1 et 2 de Lotka-Volterra. Les cycles véhiculés par les équations 5 et 6 peuvent avoir une amplitude et des densités moyennes constantes tant que le milieu est constant ; après une perturbation, ils peuvent revenir à leurs amplitudes et densités moyennes antérieures. De tels cycles qui se rétablissent après des perturbations sont appelés cycles limites stables. L'interaction entre un lièvre et un lynx peut être considérée comme un cycle limite stable, mais ce n'est pas un cycle de Lotka-Volterra.[...]
Considérons l'apparition d'une instabilité de diffusion dans le système prédateur-proie, mais nous allons d'abord écrire les conditions qui assurent l'apparition d'une instabilité de diffusion dans le système (1.1) avec n = 2. Il est clair que l'équilibre (N, N ) est local (c'est-à-dire[ .. .]
Passons à l'interprétation des cas associés à la coexistence à long terme d'un prédateur et d'une proie. Il est clair qu'en l'absence de cycles limites, un équilibre stable correspondra aux fluctuations de population dans un environnement aléatoire, et leur amplitude sera proportionnelle à la dispersion des perturbations. Ce phénomène se produira si le prédateur a une mortalité relative élevée et en même temps un degré élevé d'adaptabilité à une proie donnée.[...]
Considérons maintenant comment la dynamique du système change avec l'augmentation de la condition physique du prédateur, c'est-à-dire avec b décroissant de 1 à 0. Si la condition physique est suffisamment faible, alors il n'y a pas de cycles limites et l'équilibre est instable. Avec une augmentation de la condition physique au voisinage de cet équilibre, un cycle stable puis un cycle externe instable peuvent apparaître. En fonction des conditions initiales (le rapport entre la biomasse des prédateurs et celle des proies), le système peut soit perdre sa stabilité, c'est-à-dire quitter le voisinage de l’équilibre, sinon des oscillations stables s’y établiront au fil du temps. Une croissance ultérieure de la condition physique rend impossible la nature oscillatoire du comportement du système. Cependant, lorsque b [...]
Un exemple de rétroaction négative (stabilisatrice) est la relation entre prédateur et proie ou le fonctionnement du système carboné océanique (solution de CO2 dans l'eau : CO2 + H2O -> H2CO3). Généralement, la quantité de dioxyde de carbone dissoute dans l’eau des océans est en équilibre partiel avec la concentration de dioxyde de carbone dans l’atmosphère. Les augmentations locales du dioxyde de carbone dans l'atmosphère après les éruptions volcaniques conduisent à une intensification de la photosynthèse et à son absorption par le système carbonaté océanique. À mesure que les niveaux de dioxyde de carbone dans l’atmosphère diminuent, le système carbonaté océanique libère du CO2 dans l’atmosphère. Par conséquent, la concentration de dioxyde de carbone dans l’atmosphère est assez stable.[...]
[ ...]
Comme le note R. Ricklefs (1979), il existe des facteurs qui contribuent à la stabilisation des relations dans le système « prédateur-proie » : l'inefficacité du prédateur, la présence de ressources alimentaires alternatives pour le prédateur, la réduction du retard dans la la réaction du prédateur, ainsi que les restrictions environnementales imposées par l'environnement extérieur à l'une ou l'autre population. Les interactions entre les populations de prédateurs et de proies sont très variées et complexes. Ainsi, si les prédateurs sont suffisamment efficaces, ils peuvent réguler la densité de population des proies, la maintenant en dessous de la capacité de charge de l’environnement. Par l'influence qu'ils exercent sur les populations de proies, les prédateurs influencent l'évolution de diverses caractéristiques de la proie, ce qui conduit in fine à un équilibre écologique entre les populations de prédateurs et de proies.[...]
Si une des conditions est remplie : 0 1/2. Si 6 > 1 (kA [...]
La stabilité du biote et de l'environnement dépend uniquement de l'interaction des plantes - autotrophes et organismes herbivores hétérotrophes. Les prédateurs, quelle que soit leur taille, ne sont pas capables de perturber l'équilibre écologique d'une communauté, car dans des conditions naturelles, ils ne peuvent pas augmenter leur nombre avec un nombre constant de proies. Les prédateurs doivent non seulement être eux-mêmes mobiles, mais peuvent également se nourrir uniquement d'animaux en mouvement.[...]
Aucun autre poisson n'est aussi répandu que le brochet. Dans quelques zones de pêche situées dans des réservoirs stagnants ou coulants, les brochets ne subissent aucune pression pour maintenir l'équilibre entre proies et prédateurs. Seuls les réservoirs artificiels modernes, dans lesquels les brochets sont des poissons indésirables en raison de la reproduction d'autres poissons, ne sont pas délibérément peuplés par des brochets. eux. Le brochet est exceptionnellement bien représenté dans le monde. Ils sont capturés dans tout l'hémisphère nord, des États-Unis et du Canada jusqu'à Amérique du Nord, à travers l'Europe jusqu'à l'Asie du Nord.[...]
Une autre possibilité de coexistence durable apparaît ici, dans une gamme étroite d'adaptation relativement élevée. Lors de la transition vers un régime instable avec un très « bon » prédateur, un cycle limite externe stable peut apparaître, dans lequel la dissipation de la biomasse est équilibrée par son afflux dans le système (productivité élevée des proies). Ensuite, une situation curieuse se présente lorsque les plus probables sont deux valeurs caractéristiques de l'amplitude des oscillations aléatoires. Certains se produisent près de l'équilibre, d'autres près du cycle limite, et des transitions plus ou moins fréquentes entre ces régimes sont possibles.
Populations hypothétiques qui se comportent selon les vecteurs de la Fig. 10.11 A, sont illustrés à la Fig. 10.11,-B en utilisant un graphique montrant la dynamique du rapport entre les populations de prédateurs et de proies et sur la Fig. 10.11.5 sous la forme d'un graphique de la dynamique de l'abondance des prédateurs et des proies dans le temps. Dans la population de proies, à mesure qu'elle passe d'un équilibre de faible densité à un équilibre de haute densité et qu'elle revient, une « explosion » de nombres se produit. Et cette explosion numérique n’est pas la conséquence d’un changement aussi prononcé de l’environnement. Au contraire, cette évolution des chiffres est générée par l’impact lui-même (avec un faible niveau de « bruit » dans l’environnement) et reflète notamment l’existence de plusieurs états d’équilibre. Un raisonnement similaire peut être utilisé pour expliquer des cas plus complexes de dynamique de population dans les populations naturelles.[...]
La propriété la plus importante d'un écosystème est sa stabilité, l'équilibre des échanges et les processus qui s'y déroulent. La capacité des populations ou des écosystèmes à maintenir un équilibre dynamique stable dans des conditions environnementales changeantes est appelée homéostasie (homoios - identique, similaire ; stase - état). L'homéostasie est basée sur le principe du feedback. Pour maintenir l’équilibre dans la nature, aucun contrôle externe n’est requis. Un exemple d'homéostasie est le sous-système « prédateur-proie », dans lequel la densité de population des prédateurs et des proies est régulée.[...]
Un écosystème naturel (biogéocénose) fonctionne de manière stable avec l'interaction constante de ses éléments, la circulation de substances, le transfert d'énergie et d'informations chimiques, énergétiques, génétiques et autres à travers des chaînes-canaux. Selon le principe d’équilibre, tout système naturel traversé par un flux d’énergie et d’informations a tendance à développer un état stable. Dans le même temps, la stabilité des écosystèmes est assurée automatiquement grâce à un mécanisme de rétroaction. Le feedback consiste à utiliser les données reçues des composantes gérées des écosystèmes pour apporter des ajustements au processus par les composantes gestionnaires. La relation « prédateur »-« proie » discutée ci-dessus dans ce contexte peut être décrite de manière un peu plus détaillée ; oui, dans un écosystème aquatique poisson prédateur(brochet dans un étang) mange d'autres espèces de poissons proies (carpe carassin) ; si le nombre de carassins augmente, c'est un exemple de rétroaction positive ; le brochet, se nourrissant de carassins, réduit son nombre - c'est un exemple de rétroaction négative ; à mesure que le nombre de prédateurs augmente, le nombre de victimes diminue et le prédateur, confronté à un manque de nourriture, réduit également la croissance de sa population ; au final, dans l'étang en question, un équilibre dynamique s'établit entre les effectifs de brochets et de carassins. Un équilibre est constamment maintenu, ce qui exclurait la disparition de tout maillon de la chaîne trophique (Fig. 64).[...]
Passons à la généralisation la plus importante, à savoir que les interactions négatives deviennent moins perceptibles avec le temps si l'écosystème est suffisamment stable et si sa structure spatiale permet l'adaptation mutuelle des populations. Dans les systèmes modèles comme chasseur chassé, décrit par l'équation de Lotka-Volterra, si des termes supplémentaires ne sont pas introduits dans l'équation, caractérisant l'action des facteurs d'autolimitation des nombres, alors les oscillations se produisent de manière continue et ne s'éteignent pas (voir Lewontin, 1969). Pimentel (1968 ; voir aussi Pimentel et Stone, 1968) a montré expérimentalement que de tels termes supplémentaires peuvent refléter des adaptations mutuelles ou des changements génétiques. retour. Lorsque de nouvelles cultures ont été créées à partir d'individus qui avaient coexisté pendant deux ans dans une culture où leur nombre était soumis à des fluctuations importantes, il s'est avéré qu'elles ont développé une homéostasie écologique, dans laquelle chacune des populations était « supprimée » par l'autre à un tel point. à tel point qu'il s'est avéré possible leur coexistence dans un équilibre plus stable.
Modèle de situation prédateur-proie
Considérons un modèle mathématique de la dynamique de coexistence de deux espèces biologiques (populations) interagissant entre elles selon le type « prédateur-proie » (loups et lapins, brochets et carassins, etc.), appelé modèle Volter-Lotka. . Il a été obtenu pour la première fois par A. Lotka (1925), et un peu plus tard et indépendamment de Lotka, des modèles similaires et plus complexes ont été développés par le mathématicien italien V. Volterra (1926), dont les travaux ont en fait jeté les bases de ce qu'on appelle écologie mathématique.
Supposons qu'il y ait deux espèces biologiques qui vivent ensemble dans un environnement isolé. Cela suppose :
- 1. La victime peut trouver suffisamment de nourriture pour survivre ;
- 2. Chaque fois qu'une proie rencontre un prédateur, ce dernier tue la victime.
Pour plus de précision, nous les appellerons carassins et brochets. Laisser
l'état du système est déterminé par les quantités x(t) Et yt)- le nombre de carassins et de brochets à la fois G. Pour obtenir des équations mathématiques décrivant approximativement la dynamique (évolution dans le temps) d’une population, nous procédons comme suit.
Comme dans le modèle de croissance démographique précédent (voir section 1.1), pour les victimes nous avons l’équation
Où UN> 0 (le taux de natalité dépasse le taux de mortalité)
Coefficient UN l'augmentation des proies dépend du nombre de prédateurs (diminue avec leur augmentation). Dans le cas le plus simple a- a - fjy (a>0, p>0). Ensuite, pour la taille de la population de proies, nous avons l'équation différentielle
Pour une population de prédateurs nous avons l'équation

Où b>0 (la mortalité dépasse le taux de natalité).
Coefficient b Le déclin des prédateurs est réduit s’il y a des proies dont se nourrir. Dans le cas le plus simple, nous pouvons prendre b - y -Sx (y > 0, S> 0). Ensuite, pour la taille de la population de prédateurs, nous obtenons l'équation différentielle

Ainsi, les équations (1.5) et (1.6) représentent un modèle mathématique du problème de l'interaction de population considéré. Dans ce modèle, les variables x,y est l'état du système et les coefficients caractérisent sa structure. Le système non linéaire (1.5), (1.6) est le modèle Voltaire-Lotka.
Les équations (1.5) et (1.6) doivent être complétées par des conditions initiales - données données des populations initiales.
Analysons maintenant le modèle mathématique construit.
Construisons le portrait de phase du système (1.5), (1.6) (au sens du problème X> 0, v >0). En divisant l'équation (1.5) par l'équation (1.6), on obtient une équation à variables séparables
En utilisant cette équation, nous avons
La relation (1.7) donne l'équation des trajectoires de phase sous forme implicite. Le système (1.5), (1.6) a un état stationnaire déterminé à partir de

A partir des équations (1.8) nous obtenons (puisque l* F 0, oui* F 0)
Les égalités (1.9) déterminent la position d'équilibre (point À PROPOS DE)(Fig. 1.6).

La direction du mouvement le long de la trajectoire de phase peut être déterminée à partir de ces considérations. Qu'il y ait peu de carassins. par ex. x ~ 0, puis d'après l'équation (1.6) y
Toutes les trajectoires de phase (sauf le point 0) courbes fermées couvrant la position d’équilibre. L'état d'équilibre correspond à un nombre constant de x" et y" de carassins et de brochets. Les carassins se multiplient, les brochets les mangent, meurent, mais leur nombre et celui des autres ne change pas. "Les trajectoires en phase fermée correspondent à un changement périodique du nombre de carassins et de brochets. De plus, la trajectoire le long de laquelle se déplace le point de phase dépend des conditions initiales. Considérons comment l'état change le long de la trajectoire de phase. Soit le point dans la position UN(Fig. 1.6). Il y a ici peu de carassins, beaucoup de brochets ; les brochets n'ont rien à manger, ils disparaissent progressivement et presque
disparaître complètement. Mais le nombre de carassins diminue également presque jusqu'à zéro et
seulement plus tard, quand il y avait moins de brochets que à, le nombre de carassins commence à augmenter ; leur taux de croissance augmente et leur nombre augmente - cela se produit jusqu'au point DANS. Mais une augmentation du nombre de carassins entraîne un ralentissement du processus d'extinction du shuk et leur nombre commence à augmenter (il y a plus de nourriture) - intrigue Soleil. Ensuite il y a beaucoup de brochets, ils mangent des carassins et les mangent presque tous (section CD). Après cela, les brochets recommencent à mourir et le processus se répète sur une période d'environ 5 à 7 ans. En figue. 1.7 courbes qualitativement construites d'évolution du nombre de carassins et de brochets en fonction du temps. Les maximums des courbes alternent et le nombre maximum de brochets est en retard par rapport aux maximums de carassins.

Ce comportement est typique de divers systèmes prédateurs-proies. Interprétons maintenant les résultats obtenus.
Malgré le fait que le modèle considéré soit le plus simple et qu'en réalité tout se passe beaucoup plus compliqué, il a permis d'expliquer certaines des choses mystérieuses qui existent dans la nature. Les histoires des pêcheurs sur les périodes où « les brochets eux-mêmes sautent entre leurs mains » sont compréhensibles ; la fréquence des maladies chroniques, etc., a été expliquée.
Notons encore un conclusion intéressante, qui peut être réalisé à partir de la Fig. 1.6. Si au point R. il y a une capture rapide des brochets (dans une autre terminologie - tir aux loups), puis le système « saute » au point Q, et un mouvement supplémentaire se produit le long d'une trajectoire fermée de plus petite taille, ce qui est intuitivement attendu. Si l'on réduit le nombre de brochets en un point R, alors le système ira au point S, et d'autres mouvements se produiront le long de la trajectoire plus grande taille. Les amplitudes des oscillations vont augmenter. C’est contre-intuitif, mais cela explique précisément ce phénomène : suite aux tirs sur les loups, leur nombre augmente avec le temps. Ainsi, le choix du moment de la prise de vue est important dans ce cas.
Supposons que deux populations d'insectes (par exemple, un puceron et une coccinelle, qui se nourrissent de pucerons) soient en équilibre naturel. x-x*,y = y*(point À PROPOS En figue. 1.6). Considérez l’effet d’une seule application d’un insecticide qui tue x> 0 des victimes et y > 0 des prédateurs sans les détruire complètement. Une diminution du nombre des deux populations conduit au fait que le point représentant de la position À PROPOS"sautera" plus près de l'origine des coordonnées, où x> 0, y 0 (Fig. 1.6) Il s'ensuit que sous l'action d'un insecticide destiné à détruire les victimes (pucerons), le nombre de victimes (pucerons) augmente et le nombre de prédateurs ( coccinelles) diminue. Il s'avère que le nombre de prédateurs peut devenir si petit qu'ils risquent une extinction complète pour d'autres raisons (sécheresse, maladie, etc.). Ainsi, l'utilisation d'insecticides (à moins qu'ils ne détruisent presque complètement les insectes nuisibles) conduit finalement à une augmentation de la population d'insectes dont le nombre était contrôlé par d'autres insectes prédateurs. De tels cas sont décrits dans des livres de biologie.
D'une manière générale, le taux de croissance du nombre de victimes UN dépend à la fois de "L" et de y : UN= a(x, y) (en raison de la présence de prédateurs et des restrictions alimentaires).
Avec un petit changement dans le modèle (1.5), (1.6), des petits termes sont ajoutés aux membres de droite des équations (en tenant compte, par exemple, de la compétition du carassin pour la nourriture et du brochet pour le carassin)
ici 0 f.i « 1.
Dans ce cas, la conclusion sur la périodicité du processus (le retour du système à son état d'origine), valable pour les modèles (1.5), (1.6), perd sa validité. Selon le type de petites modifications/ et g Les situations illustrées à la Fig. sont possibles. 1.8.

Dans le cas (1) l'état d'équilibre À PROPOS durable. Pour toute autre condition initiale, après suffisamment temps fort C'est ce qui est installé.
Dans le cas (2), le système « tombe en désarroi ». L'état stationnaire est instable. Un tel système s’inscrit finalement dans une telle gamme de valeurs X et y que le modèle cesse d'être applicable.
Dans le cas (3) dans un système avec un état stationnaire instable À PROPOS Un régime périodique s'établit au fil du temps. Contrairement au modèle original (1.5), (1.6), dans ce modèle, le régime périodique en régime permanent ne dépend pas des conditions initiales. Initialement faible écart par rapport à l’état stable À PROPOS n'entraîne pas de petites fluctuations autour À PROPOS, comme dans le modèle Volterra-Lotka, mais à des oscillations d'amplitude bien définie (et indépendante de la petitesse de l'écart).
DANS ET. Arnold qualifie le modèle Volterra-Lotka de rigide parce que son petit changement peut conduire à des conclusions différentes de celles données ci-dessus. Pour juger laquelle des situations illustrées à la Fig. 1.8, implémenté dans ce système, est absolument nécessaire Informations Complémentaires sur le système (sur le type de petits amendements/ et g).
Ici, contrairement à (3.2.1), les signes de (-012) et (+a2i) sont différents. Comme dans le cas de la compétition (système d'équations (2.2.1)), l'origine des coordonnées (1) pour ce système est un point particulier de type « nœud instable ». Trois autres états stationnaires possibles :

La signification biologique nécessite des quantités positives Xyx 2. Pour l'expression (3.3.4), cela signifie que
Si le coefficient de compétition intraspécifique des prédateurs UN,22 = 0, la condition (3.3.5) conduit à la condition ai2
Les types possibles de portraits de phase pour le système d'équations (3.3.1) sont présentés dans la Fig. 3.2 a-c. Les isoclines des tangentes horizontales sont des lignes droites
et les isoclines des tangentes verticales sont droites
De la fig. 3.2 montre ce qui suit. Le système prédateur-proie (3.3.1) peut avoir une position d’équilibre stable dans laquelle la population de proies est complètement éteinte. (x = 0) et seuls les prédateurs sont restés (point 2 de la Fig. 3.26). Évidemment, une telle situation ne peut se réaliser que si, outre le type de victimes en question, X prédateur X2 dispose de sources d'alimentation supplémentaires. Ce fait est reflété dans le modèle par un terme positif à droite de l’équation pour xs. Les points singuliers (1) et (3) (Fig. 3.26) sont instables. La deuxième possibilité est un état stationnaire stable, dans lequel la population de prédateurs a complètement disparu et il ne reste que les proies - point stable (3) (Fig. 3.2a). Ici le point singulier (1) est aussi un nœud instable.
Enfin, la troisième possibilité est la coexistence stable de populations de prédateurs et de proies (Fig. 3.2 c), dont les effectifs stationnaires sont exprimés par des formules (3.3.4). Considérons ce cas plus en détail.
Supposons que les coefficients de compétition intraspécifique soient égaux à zéro (ai= 0, je = 1, 2). Supposons également que les prédateurs se nourrissent uniquement de proies de l'espèce X et en leur absence ils meurent au rythme de C2 (en (3.3.5) C2
Menons une étude détaillée de ce modèle, en utilisant la notation la plus largement acceptée dans la littérature. Remise à neuf

Riz. 3.2. La localisation des principales isoclines sur le portrait de phase du système prédateur-proie de Volterra pour différents ratios de paramètres : UN- à propos -
AVEC je C2 C2
1, 3 - instable, 2 - point singulier stable ; V-
1, 2, 3 - instable, 4 - point singulier stable significatif
Le système prédateur-proie dans ces notations a la forme :

Nous étudierons les propriétés des solutions du système (3.3.6) sur le plan des phases N1
SUR2
Le système dispose de deux solutions stationnaires. Ils peuvent être facilement déterminés en assimilant les membres droits du système à zéro. On a: 
D'où les solutions stationnaires :

Examinons de plus près la deuxième solution. Trouvons la première intégrale du système (3.3.6), ne contenant pas t. Multiplions la première équation par -72, la seconde par -71 et additionnons les résultats. On a:
Divisons maintenant la première équation par N et multiplier par € 2, et divisez le second par JV 2 et multipliez par e. Ajoutons à nouveau les résultats :
En comparant (3.3.7) et (3.3.8), nous aurons :

En intégrant, on obtient :

C'est la première intégrale souhaitée. Ainsi, le système (3.3.6) est conservateur car il possède une première intégrale de mouvement, une quantité qui est fonction des variables du système. N Et N2 et indépendant du temps. Cette propriété permet de construire pour les systèmes Volterra un système de concepts similaire à la mécanique statistique (voir chapitre 5), où la valeur énergétique du système, constante dans le temps, joue un rôle important.
Pour chaque fixe de > 0 (qui correspond à certaines données initiales), l'intégrale correspond à une certaine trajectoire dans le plan N1 SUR2 , servant de trajectoire au système (3.3.6).
Considérons méthode graphique construction de trajectoire, proposée par Volterra lui-même. remarquerez que partie droite la formule (3.3.9) ne dépend que de D g 2, et celle de gauche ne dépend que de N. Notons
De (3.3.9) il résulte qu’entre X Et Oui il y a une relation proportionnelle
En figue. 3.3 montre les premiers quadrants de quatre systèmes de coordonnées XOY,NOY, N2 BŒUF et D G 1 0N2 de sorte qu'ils ont tous une origine commune.
Dans le coin supérieur gauche (quadrant NON) un graphique de la fonction (3.3.8) est tracé, en bas à droite (quadrant N2 BŒUF)- graphique de fonction Y. La première fonction a min à Ni = et le second - max à N2 = ?-
Enfin, dans le quadrant XOY construisons une droite (3.3.12) pour un certain AVEC.
Marquons le point N sur l'axe SUR. Ce point correspond à une certaine valeur O(N 1), facile à retrouver en traçant une perpendiculaire

Riz. 3.3.
à travers N jusqu'à ce qu'elle croise la courbe (3.3.10) (voir Fig. 3.3). À son tour, la valeur K(D^) correspond à un certain point M sur la droite Oui = CX et donc une certaine valeur X(N) = O(N)/c, que l'on peut trouver en traçant des perpendiculaires SUIS. Et MARYLAND. La valeur trouvée (ce point est marqué sur la figure par la lettre D) deux points correspondent R. Et g sur la courbe (3.3.11). En utilisant ces points, en traçant des perpendiculaires, nous trouverons deux points à la fois E" Et E", couché sur la courbe (3.3.9). Leurs coordonnées :

Tracer une perpendiculaire SUIS., nous avons franchi la courbe (3.3.10) en un point supplémentaire DANS. Ce point correspond au même R. Et Q sur la courbe (3.3.11) et pareil N Et SCH. Coordonner N ce point peut être trouvé en laissant tomber la perpendiculaire de DANS par axe SUR. Nous obtenons donc les points F" et F", se trouvant également sur la courbe (3.3.9).
Venant d'un point différent N, de la même manière on obtient quatre nouveaux points situés sur la courbe (3.3.9). L'exception sera le point Ni= ?2/72- Sur cette base, nous obtenons seulement deux points : À Et L. Ce seront les points inférieurs et supérieurs de la courbe (3.3.9).
Je ne peux pas partir de valeurs N, et à partir des valeurs N2 . En provenance de N2 à la courbe (3.3.11), puis en remontant jusqu'à la droite Y = cX, et de là traversant la courbe (3.3.10), on retrouve également quatre points de la courbe (3.3.9). L'exception sera le point Non=?1/71- Sur cette base, nous obtenons seulement deux points : g Et À. Ce seront les points les plus à gauche et à droite de la courbe (3.3.9). En demandant différemment N Et N2 et après avoir reçu pas mal de points, les reliant, nous allons construire approximativement la courbe (3.3.9).
De la construction il ressort clairement qu'il s'agit d'une courbe fermée contenant en elle le point 12 = (?2/721?1/71)” à partir de certaines données initiales N Yu et N20. En prenant une autre valeur de C, c'est-à-dire d'autres données initiales, on obtient une autre courbe fermée qui ne coupe pas la première et contient également le point (?2/721 ?1/71)1 à l'intérieur d'elle-même. Ainsi, la famille de trajectoires (3.3.9) est une famille de lignes fermées entourant le point 12 (voir Fig. 3.3). Etudions le type de stabilité de ce point singulier en utilisant la méthode de Lyapunov.
Puisque tous les paramètres e 1, ?2, 71,72 sont positifs, point final (N[ est situé dans le quadrant positif du plan de phase. La linéarisation du système près de ce point donne :

Ici NT) et 7i2(N1, N2 :
Équation caractéristique du système (3.3.13) :

Les racines de cette équation sont purement imaginaires :

Ainsi, une étude du système montre que les trajectoires proches du point singulier sont représentées par des ellipses concentriques, et que le point singulier lui-même est le centre (Fig. 3.4). Le modèle Volterra considéré présente également des trajectoires fermées loin du point singulier, bien que la forme de ces trajectoires soit déjà différente d'ellipsoïdale. Comportement des variables Ni, N2 au fil du temps est montré sur la Fig. 3.5.

Riz. 3.4.

Riz. 3.5. Dépendance du nombre de proies N moi et le prédateur N2 de temps
Un point singulier de type central est stable, mais pas asymptotiquement. Montrons avec cet exemple ce que c'est. Laisse l'hésitation Lente) et LGgM se produisent de telle manière que le point représentatif se déplace le long du plan de phase le long de la trajectoire 1 (voir Fig. 3.4). Au moment où le point est en position M, un certain nombre d'individus sont ajoutés au système depuis l'extérieur N 2, de telle sorte que le point représentatif saute du point M au point A/". Ensuite, si le système est à nouveau laissé à lui-même, les oscillations Ni Et N2 se produira déjà avec des amplitudes plus grandes qu'auparavant, et le point représentatif se déplace le long de la trajectoire 2. Cela signifie que les oscillations dans le système sont instables : elles changent pour toujours leurs caractéristiques lorsque influence externe. À l’avenir, nous considérerons des modèles décrivant des régimes oscillatoires stables et montrerons que sur le plan des phases, de tels mouvements périodiques asymptotiques et stables sont représentés à l’aide de cycles limites.
En figue. La figure 3.6 montre les courbes expérimentales - fluctuations du nombre d'animaux à fourrure au Canada (selon la Compagnie de la Baie d'Hudson). Ces courbes sont construites à partir des données relatives au nombre de peaux récoltées. Les périodes de fluctuations du nombre de lièvres (proies) et de lynx (prédateurs) sont à peu près les mêmes et sont de l'ordre de 9 à 10 ans. Dans ce cas, le nombre maximum de lièvres est, en règle générale, en avance d'un an sur le nombre maximum de lynx.
La forme de ces courbes expérimentales est beaucoup moins régulière que celle théorique. Cependant, dans ce cas, il suffit que le modèle assure la coïncidence des caractéristiques les plus significatives des courbes théoriques et expérimentales, c'est-à-dire valeurs d'amplitude et déphasages entre les fluctuations du nombre de prédateurs et de proies. Un inconvénient beaucoup plus grave du modèle Volterra est l'instabilité des solutions du système d'équations. En effet, comme mentionné ci-dessus, tout changement aléatoire dans l'abondance de l'une ou l'autre espèce devrait conduire, selon le modèle, à une modification de l'amplitude des oscillations des deux espèces. Naturellement, dans conditions naturelles les animaux sont soumis à d’innombrables influences aléatoires. Comme le montrent les courbes expérimentales, l’amplitude des fluctuations du nombre d’espèces varie peu d’une année à l’autre.
Le modèle de Volterra est une référence (de base) pour l'écologie mathématique au même titre que le modèle de l'oscillateur harmonique est fondamental pour l'écologie mathématique classique et mécanique quantique. En utilisant ce modèle, basé sur des idées très simplifiées sur la nature des modèles qui décrivent le comportement du système, purement mathématique
chapitre 3

Riz. 3.6. Courbes cinétiques du nombre d'animaux à fourrure selon les données de la Hudson Bay Fur Company (Seton-Thomson, 1987) Au moyen d'une conclusion a été tirée sur la nature qualitative du comportement d'un tel système - sur la présence de fluctuations de la population dans un tel système. Sans construire un modèle mathématique et sans l’utiliser, une telle conclusion serait impossible.
Dans ce dont nous avons discuté ci-dessus sous forme simple Le système Volterra présente deux inconvénients fondamentaux et interdépendants. Une abondante littérature écologique et mathématique est consacrée à leur « élimination ». Premièrement, l’inclusion de facteurs supplémentaires, aussi petits soient-ils, dans le modèle modifie qualitativement le comportement du système. Le deuxième inconvénient « biologique » du modèle est qu'il n'intègre pas les propriétés fondamentales inhérentes à tout couple de populations interagissant selon le principe prédateur-proie : l'effet de saturation du prédateur, les ressources limitées du prédateur et même de la proie. avec un excès de proies, la possibilité d'un nombre minimum de proies disponibles pour le prédateur, etc.
Afin d'éliminer ces lacunes, diverses modifications du système Volterra ont été proposées par différents auteurs. Les plus intéressants d’entre eux seront abordés dans la section 3.5. Ici, nous nous concentrerons uniquement sur un modèle qui prend en compte les auto-limitations dans la croissance des deux populations. L'exemple de ce modèle montre clairement comment la nature des décisions peut changer lorsque les paramètres du système changent.
On considère donc le système

Le système (3.3.15) diffère du système considéré précédemment (3.3.6) par la présence de termes de la forme -7 sur les membres droits des équations UNF,
Ces termes reflètent le fait que la population de proies ne peut pas croître indéfiniment même en l'absence de prédateurs en raison de ressources alimentaires limitées et d'un habitat limité. Les mêmes « auto-restrictions » sont imposées à la population de prédateurs.
Pour trouver des nombres stationnaires d’espèces iVi et N2 Égalisons les membres droits des équations du système (3.3.15) à zéro. Les solutions avec un nombre nul de prédateurs ou de proies ne nous intéresseront pas pour l’instant. Par conséquent, considérons le système algébrique
équations  Sa décision
Sa décision
nous donne les coordonnées du point singulier. Ici, la condition de positivité des nombres stationnaires doit être imposée aux paramètres du système : N> 0 et N2 > 0. Les racines de l'équation caractéristique du système linéarisé au voisinage du point singulier (3.3.16) :

D'après l'expression des nombres caractéristiques, il ressort clairement que si la condition est remplie
alors le nombre de prédateurs et de proies subit des oscillations amorties au fil du temps, le système a un point singulier non nul et un foyer stable. Le portrait de phase d'un tel système est présenté sur la Fig. 3,7 a.
Supposons que les paramètres de l'inégalité (3.3.17) changent leurs valeurs de telle manière que la condition (3.3.17) devienne égalité. Alors les nombres caractéristiques du système (3.3.15) sont égaux et son point singulier se situera à la frontière entre les régions des foyers stables et des nœuds. Lorsque le signe de l'inégalité (3.3.17) s'inverse, le point singulier devient un nœud stable. Le portrait de phase du système pour ce cas est présenté sur la Fig. 3.76.
Comme dans le cas d’une population unique, un modèle stochastique peut être développé pour le modèle (3.3.6), mais une solution explicite ne peut pas être obtenue pour celui-ci. Nous nous limiterons donc à des considérations générales. Supposons par exemple que le point d'équilibre soit situé à une certaine distance de chacun des axes. Puis pour les trajectoires de phase sur lesquelles les valeurs de JVj, N2 restent suffisamment grands, un modèle déterministe sera tout à fait satisfaisant. Mais si à un moment donné


Riz. 3.7. Portrait de phase du système (3.3.15) : UN - lorsque la relation (3.3.17) entre les paramètres est satisfaite ; b- lors de l'exécution d'une relation inverse entre les paramètres
trajectoire de phase, toute variable n'est pas très grande, alors les fluctuations aléatoires peuvent devenir significatives. Ils conduisent au fait que le point représentatif se déplace vers l'un des axes, ce qui entraîne l'extinction de l'espèce correspondante. Ainsi, le modèle stochastique s'avère instable, puisque la « dérive » stochastique conduit tôt ou tard à l'extinction de l'une des espèces. Dans ce type de modèle, le prédateur finit par disparaître, soit par hasard, soit parce que sa population de proies est éliminée en premier. Le modèle stochastique du système prédateur-proie explique bien les expériences de Gause (Gause, 1934 ; 2000), dans lesquelles les ciliés Paramettum candatum servi de victime à un autre cilié Didinium nasatum- prédateur. Les nombres d'équilibre attendus selon les équations déterministes (3.3.6) dans ces expériences n'étaient que d'environ cinq individus de chaque espèce, il n'est donc pas surprenant que dans chaque expérience répétée, soit les prédateurs, soit les proies disparaissent assez rapidement (et ensuite les prédateurs) .
Ainsi, l'analyse des modèles Volterra d'interaction entre les espèces montre que, malgré la grande variété de types de comportement de tels systèmes, il ne peut y avoir de fluctuations non amorties du nombre dans le modèle d'espèces concurrentes. Dans le modèle prédateur-proie, les oscillations non amorties apparaissent comme le résultat d'un choix formulaire spécialéquations modèles (3.3.6). Dans ce cas, le modèle devient non brut, ce qui indique l'absence dans un tel système de mécanismes cherchant à préserver son état. Cependant, de telles oscillations sont observées dans la nature et expérimentalement. La nécessité de leur explication théorique a été l'une des raisons pour lesquelles des descriptions de modèles ont été formulées de manière plus approfondie. vue générale. La section 3.5 est consacrée à l’examen de ces modèles généralisés.