Ταλαντώσεις του συστήματος αρπακτικών-θηραμάτων (μοντέλο Lotka-Volter). Μαθήματα: Ποιοτική μελέτη του μοντέλου αρπακτικού-θηράματος Μαθηματικό μοντέλο του συστήματος αρπακτικών-θηραμάτων
Μοντέλα αλληλεπίδρασης δύο ειδών
Υποθέσεις της Volterra. Αναλογίες με χημική κινητική. Μοντέλα αλληλεπιδράσεων Volterra. Ταξινόμηση τύπων αλληλεπιδράσεων Διαγωνισμός. Αρπακτικό-θήραμα. Γενικευμένα μοντέλα αλληλεπίδρασης ειδών . Μοντέλο Κολμογκόροφ. Το μοντέλο του MacArthur για την αλληλεπίδραση μεταξύ δύο ειδών εντόμων. Παραμετρική και πορτρέτα φάσης του συστήματος Bazykin.
Ο Ιταλός μαθηματικός Vito Volterra θεωρείται δικαίως ο ιδρυτής της σύγχρονης μαθηματικής θεωρίας των πληθυσμών, ο οποίος ανέπτυξε τη μαθηματική θεωρία των βιολογικών κοινοτήτων, η συσκευή της οποίας είναι οι διαφορικές και ολοκληρο-διαφορικές εξισώσεις.(Vito Volterra. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. Παρίσι, 1931). Τις επόμενες δεκαετίες, η δυναμική του πληθυσμού αναπτύχθηκε κυρίως σύμφωνα με τις ιδέες που εκφράζονται σε αυτό το βιβλίο. Η ρωσική μετάφραση του βιβλίου του Volterra εκδόθηκε το 1976 με τον τίτλο «Mathematical Theory of the Struggle for Existence» με μετάλογο του Yu.M. Svirezhev, το οποίο συζητά την ιστορία της ανάπτυξης της μαθηματικής οικολογίας την περίοδο 1931-1976.
Το βιβλίο του Volterra είναι γραμμένο με τον ίδιο τρόπο που γράφονται τα βιβλία για τα μαθηματικά. Διατυπώνει αρχικά κάποιες υποθέσεις για τα μαθηματικά αντικείμενα που υποτίθεται ότι θα μελετηθούν και στη συνέχεια πραγματοποιείται μια μαθηματική μελέτη των ιδιοτήτων αυτών των αντικειμένων.
Τα συστήματα που μελετήθηκαν από τη Volterra αποτελούνται από δύο ή περισσότερα είδη. Σε ορισμένες περιπτώσεις, λαμβάνεται υπόψη το απόθεμα των χρησιμοποιούμενων τροφίμων. Οι εξισώσεις που περιγράφουν την αλληλεπίδραση αυτών των ειδών βασίζονται στις ακόλουθες παραστάσεις.
Υποθέσεις της Volterra
1. Τα τρόφιμα είτε διατίθενται σε απεριόριστες ποσότητες, είτε η προμήθεια του με την πάροδο του χρόνου είναι αυστηρά ρυθμισμένη.
2. Τα άτομα κάθε είδους πεθαίνουν με τέτοιο τρόπο ώστε ένα σταθερό ποσοστό υπαρχόντων ατόμων να χάνεται ανά μονάδα χρόνου.
3. Τα αρπακτικά είδη τρώνε θήραμα, και σε μια μονάδα χρόνου ο αριθμός των θηραμάτων που καταναλώνονται είναι πάντα ανάλογος με την πιθανότητα να συναντηθούν άτομα αυτών των δύο ειδών, δηλ. το γινόμενο του αριθμού των αρπακτικών και του αριθμού των θηραμάτων.
4. Εάν υπάρχει τροφή σε περιορισμένες ποσότητες και πολλά είδη που μπορούν να την καταναλώσουν, τότε η αναλογία της τροφής που καταναλώνεται από ένα είδος ανά μονάδα χρόνου είναι ανάλογη με τον αριθμό των ατόμων αυτού του είδους, λαμβανόμενη με συγκεκριμένο συντελεστή ανάλογα με το είδος (μοντέλα διαειδικού ανταγωνισμού).
5. Εάν ένα είδος τρέφεται με τροφή που είναι διαθέσιμη σε απεριόριστες ποσότητες, η αύξηση του αριθμού των ειδών ανά μονάδα χρόνου είναι ανάλογη με τον αριθμό του είδους.
6. Εάν ένα είδος τρέφεται με τροφή που είναι διαθέσιμη σε περιορισμένες ποσότητες, τότε η αναπαραγωγή του ρυθμίζεται από το ποσοστό κατανάλωσης τροφής, δηλ. ανά μονάδα χρόνου, η αύξηση είναι ανάλογη με την ποσότητα του φαγητού που καταναλώνεται.
Αναλογίες με χημική κινητική
Αυτές οι υποθέσεις έχουν στενά παράλληλα με τη χημική κινητική. Στις εξισώσεις της πληθυσμιακής δυναμικής, όπως και στις εξισώσεις της χημικής κινητικής, χρησιμοποιείται η «αρχή των συγκρούσεων», όταν ο ρυθμός αντίδρασης είναι ανάλογος με το γινόμενο των συγκεντρώσεων των συστατικών που αντιδρούν.
Πράγματι, σύμφωνα με τις υποθέσεις του Volterra, η ταχύτηταεπεξεργάζομαι, διαδικασία η εξαφάνιση κάθε είδους είναι ανάλογη με την αφθονία του είδους. Στη χημική κινητική, αυτό αντιστοιχεί σε μια μονομοριακή αντίδραση αποσύνθεσης κάποιας ουσίας, και σε ένα μαθηματικό μοντέλο, σε αρνητικούς γραμμικούς όρους στη δεξιά πλευρά των εξισώσεων.
Σύμφωνα με τις έννοιες της χημικής κινητικής, ο ρυθμός μιας διμοριακής αντίδρασης της αλληλεπίδρασης δύο ουσιών είναι ανάλογος με την πιθανότητα σύγκρουσης αυτών των ουσιών, δηλ. το γινόμενο της συγκέντρωσής τους. Με τον ίδιο τρόπο, σύμφωνα με τις υποθέσεις του Volterra, ο ρυθμός αναπαραγωγής των αρπακτικών (θάνατος θηράματος) είναι ανάλογος με την πιθανότητα συναντήσεων μεταξύ αρπακτικού και θηράματος, δηλ. το γινόμενο των αριθμών τους. Και στις δύο περιπτώσεις, οι διγραμμικοί όροι εμφανίζονται στο σύστημα του μοντέλου στη δεξιά πλευρά των αντίστοιχων εξισώσεων.
Τέλος, οι γραμμικοί θετικοί όροι στη δεξιά πλευρά των εξισώσεων Volterra, που αντιστοιχούν στην αύξηση του πληθυσμού υπό απεριόριστες συνθήκες, αντιστοιχούν στους αυτοκαταλυτικούς όρους χημικές αντιδράσεις. Μια τέτοια ομοιότητα εξισώσεων σε χημικά και οικολογικά μοντέλα καθιστά δυνατή την εφαρμογή των ίδιων ερευνητικών μεθόδων για τη μαθηματική μοντελοποίηση της κινητικής του πληθυσμού όπως και για τα συστήματα χημικών αντιδράσεων.
Ταξινόμηση τύπων αλληλεπιδράσεων
Σύμφωνα με τις υποθέσεις του Volterra, η αλληλεπίδραση δύο ειδών, ο αριθμός των οποίων Χ 1 και Χ 2 μπορεί να περιγραφεί από τις εξισώσεις:
(9.1)
Εδώ οι παράμετροι ένα Εγώ - σταθερές ρυθμού ανάπτυξης των ειδών, ντο Εγώ- πληθυσμιακές αυτοπεριοριζόμενες σταθερές (ενδοειδικός ανταγωνισμός), b ij- σταθερές αλληλεπίδρασης ειδών, (Εγώ, j= 1,2). Τα σημάδια αυτών των συντελεστών καθορίζουν το είδος της αλληλεπίδρασης.
Στη βιολογική βιβλιογραφία, οι αλληλεπιδράσεις συνήθως ταξινομούνται σύμφωνα με τους μηχανισμούς που εμπλέκονται. Η ποικιλομορφία εδώ είναι τεράστια: διάφορες τροφικές αλληλεπιδράσεις, χημικές αλληλεπιδράσεις που υπάρχουν μεταξύ βακτηρίων και πλαγκτονικών φυκών, αλληλεπιδράσεις μυκήτων με άλλους οργανισμούς, διαδοχές φυτικών οργανισμών, ειδικότερα, που σχετίζονται με τον ανταγωνισμό για ηλιακό φωςκαι με την εξέλιξη των εδαφών κ.λπ. Μια τέτοια ταξινόμηση φαίνεται απροσδιόριστη.
μι . Ο Odum, λαμβάνοντας υπόψη τα μοντέλα που πρότεινε ο V. Volterra, πρότεινε μια ταξινόμηση όχι με μηχανισμούς, αλλά με αποτελέσματα. Σύμφωνα με αυτή την ταξινόμηση, οι σχέσεις πρέπει να αξιολογούνται ως θετικές, αρνητικές ή ουδέτερες, ανάλογα με το αν η αφθονία ενός είδους αυξάνεται, μειώνεται ή παραμένει αμετάβλητη παρουσία άλλου είδους. Στη συνέχεια, οι κύριοι τύποι αλληλεπιδράσεων μπορούν να παρουσιαστούν με τη μορφή πίνακα.
ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΕΙΔΩΝ
|
ΣΥΜΒΙΩΣΗ |
σι 12 ,σι 21 >0 |
||
|
ΚΟΜΜΕΝΣΑΛΙΣΜΟΣ |
σι 12 ,>0, σι 21 =0 |
||
|
ΘΗΡΕΥΤΗΣ-Θήραμα |
σι 12 ,>0, σι 21 <0 |
||
|
ΑΜΕΝΣΑΛΙΣΜΟΣ |
σι 12 ,=0, σι 21 <0 |
||
|
ΑΝΤΑΓΩΝΙΣΜΟΣ |
σι 12 , σι 21 <0 |
||
|
ΟΥΔΕΤΕΡΟΤΗΤΑ |
σι 12 , σι 21 =0 |
Η τελευταία στήλη δείχνει τα σημάδια των συντελεστών αλληλεπίδρασης από το σύστημα (9.1)
Εξετάστε τους κύριους τύπους αλληλεπιδράσεων
ΕΞΙΣΩΣΕΙΣ ΑΝΤΑΓΩΝΙΣΜΟΥ:
Όπως είδαμε στη Διάλεξη 6, οι εξισώσεις του διαγωνισμού είναι:
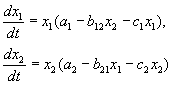 (9.2)
(9.2)
Λύσεις σταθερού συστήματος:
(1).
![]()
Η προέλευση των συντεταγμένων, για οποιεσδήποτε παραμέτρους του συστήματος, είναι ένας ασταθής κόμβος.
(2).
![]() (9.3)
(9.3)
ντο η στατική κατάσταση (9.3) είναι μια σέλα στο ένα 1 >β 12 /Με 2 και
σταθερός κόμπος στο ένα 1 12 /s 2 . Αυτή η συνθήκη σημαίνει ότι το είδος πεθαίνει εάν ο ρυθμός ανάπτυξής του είναι μικρότερος από κάποια κρίσιμη τιμή.
(3).
![]() (9.4)
(9.4)
ντο σταθερό διάλυμα (9.4)¾ σέλα στο ένα 2 >β 21 /ντο 1 και ένας σταθερός κόμπος στο ένα 2< σι 21 /ντο 1
(4).
![]() (9.5)
(9.5)
Η στατική κατάσταση (9.5) χαρακτηρίζει τη συνύπαρξη δύο ανταγωνιστικών ειδών και είναι ένας σταθερός κόμβος εάν η σχέση πληρούται:
![]()
Αυτό συνεπάγεται την ανισότητα:
σι 12
σι 21
που μας επιτρέπει να διατυπώσουμε την προϋπόθεση για τη συνύπαρξη των ειδών:
Το γινόμενο των συντελεστών αλληλεπίδρασης μεταξύ πληθυσμού είναι μικρότερο από το γινόμενο των συντελεστών αλληλεπίδρασης πληθυσμού.
Πράγματι, αφήστε τους φυσικούς ρυθμούς ανάπτυξης των δύο υπό εξέταση ειδώνένα 1 , ένα 2 είναι τα ίδια. Τότε η απαραίτητη προϋπόθεση για σταθερότητα είναι
ντο 2 > σι 12 ,ντο 1 >β 21 .
Αυτές οι ανισότητες δείχνουν ότι η αύξηση του αριθμού ενός από τους ανταγωνιστές καταστέλλει τη δική του ανάπτυξη πιο έντονα από την ανάπτυξη ενός άλλου ανταγωνιστή. Εάν η αφθονία και των δύο ειδών περιορίζεται, εν μέρει ή πλήρως, από διαφορετικούς πόρους, ισχύουν οι παραπάνω ανισότητες. Εάν και τα δύο είδη έχουν ακριβώς τις ίδιες ανάγκες, τότε ένα από αυτά θα είναι πιο βιώσιμο και θα εκτοπίσει τον ανταγωνιστή του.
Η συμπεριφορά των τροχιών φάσης του συστήματος δίνει μια οπτική αναπαράσταση των πιθανών αποτελεσμάτων του ανταγωνισμού. Εξισώνουμε τις δεξιές πλευρές των εξισώσεων του συστήματος (9.2) με μηδέν:
Χ 1 (ένα 1 - γ 1 Χ 1 – σι 12 Χ 2) = 0 (dx 1 /dt = 0),
Χ 2 (ένα 2 –σι 21 Χ 1 – ντο 2 Χ 2) = 0 (dx 2 /dt = 0),
Σε αυτή την περίπτωση, λαμβάνουμε εξισώσεις για τις κύριες ισοκλίνες του συστήματος
Χ 2 = – β 21 Χ 1 / ντο 2 +ένα 2/c2, Χ 2 = 0
είναι οι εξισώσεις ισοκλινών κατακόρυφων εφαπτομένων.
Χ 2 = – γ 1 Χ 1 /b12+ ένα 1 /σι 12 , Χ 1 = 0
είναι οι εξισώσεις ισοκλινών κατακόρυφων εφαπτομένων. Τα σημεία ζευγών τομής των ισοκλινών κατακόρυφων και οριζόντιων εφαπτομένων συστημάτων είναι σταθερές λύσεις του συστήματος των εξισώσεων (9.2.) και οι συντεταγμένες τους ![]() είναι σταθεροί αριθμοί ανταγωνιστικών ειδών.
είναι σταθεροί αριθμοί ανταγωνιστικών ειδών.
Η πιθανή θέση των κύριων ισοκλινών στο σύστημα (9.2) φαίνεται στο Σχ. 9.1. Ρύζι. 9.1ΕΝΑαντιστοιχεί στην επιβίωση του είδουςΧ 1, εικ. 9.1 σι- επιβίωση του είδουςΧ 2, εικ. 9.1 V– συνύπαρξη ειδών υπό προϋποθέσεις (9.6). Εικόνα 9.1σολδείχνει το σύστημα σκανδάλης. Εδώ το αποτέλεσμα του διαγωνισμού εξαρτάται από τις αρχικές συνθήκες. Η στατική κατάσταση (9,5), η οποία είναι μη μηδενική και για τους δύο τύπους, είναι ασταθής. Αυτή είναι η σέλα από την οποία περνά το separatrix, χωρίζοντας τις περιοχές επιβίωσης καθενός από τα είδη.

Ρύζι. 9.1.Η θέση των κύριων ισοκλινών στο πορτρέτο φάσης του συστήματος ανταγωνισμού Volterra δύο τύπων (9.2) με διαφορετικές αναλογίες παραμέτρων. Επεξηγήσεις στο κείμενο.
Για τη μελέτη του ανταγωνισμού των ειδών, πραγματοποιήθηκαν πειράματα σε διάφορους οργανισμούς. Συνήθως, επιλέγονται δύο στενά συγγενικά είδη και αναπτύσσονται μαζί και χωριστά κάτω από αυστηρά ελεγχόμενες συνθήκες. Σε ορισμένα χρονικά διαστήματα πραγματοποιείται πλήρης ή επιλεκτική απογραφή του πληθυσμού. Καταγράψτε δεδομένα από πολλά επαναλαμβανόμενα πειράματα και αναλύστε. Οι μελέτες πραγματοποιήθηκαν σε πρωτόζωα (ιδίως βλεφαρίδες), πολλά είδη σκαθαριών του γένους Tribolium, Drosophila και μαλακόστρακα του γλυκού νερού (δάφνια). Πολλά πειράματα έχουν διεξαχθεί σε μικροβιακούς πληθυσμούς (βλ. διάλεξη 11). Πειράματα πραγματοποιήθηκαν επίσης στη φύση, συμπεριλαμβανομένων των planarians (Reynolds), δύο ειδών μυρμηγκιών (Pontin) και άλλων. 9.2. φαίνονται οι καμπύλες ανάπτυξης των διατόμων που χρησιμοποιούν τον ίδιο πόρο (που καταλαμβάνουν την ίδια οικολογική θέση). Όταν καλλιεργείται σε μονοκαλλιέργεια Asteronella formosa φθάνει σε σταθερό επίπεδο πυκνότητας και διατηρεί τη συγκέντρωση του πόρου (πυριτικού) σε σταθερά χαμηλό επίπεδο. Β. Όταν καλλιεργείται σε μονοκαλλιέργειαΣυνεδράουινα συμπεριφέρεται με παρόμοιο τρόπο και διατηρεί τη συγκέντρωση πυριτικού σε ακόμη χαμηλότερο επίπεδο. Β. Με συγκαλλιέργεια (σε δύο αντίτυπα)Η Synedrauina ανταγωνίζεται την Asteronella formosa. Προφανώς η Συνέδρα

Ρύζι. 9.2.Ανταγωνισμός στα διάτομα. ΕΝΑ -όταν καλλιεργείται σε μονοκαλλιέργεια Asteronella formosa φτάνει σε σταθερό επίπεδο πυκνότητας και διατηρεί τη συγκέντρωση του πόρου (πυριτικού) σε συνεχώς χαμηλό επίπεδο. β -όταν καλλιεργείται σε μονοκαλλιέργειαΣυνεδράουινα συμπεριφέρεται με παρόμοιο τρόπο και διατηρεί τη συγκέντρωση πυριτικού σε ακόμη χαμηλότερο επίπεδο. V -σε συγκαλλιέργεια (εις διπλούν)Η Synedruina ανταγωνίζεται την Asteronella formosa. Προφανώς η Συνέδρα κερδίζει τον διαγωνισμό λόγω της ικανότητάς του να χρησιμοποιεί πληρέστερα το υπόστρωμα (βλ. επίσης Διάλεξη 11).
Τα πειράματα του G. Gause σχετικά με τη μελέτη του ανταγωνισμού είναι ευρέως γνωστά, αποδεικνύοντας την επιβίωση ενός από τα ανταγωνιστικά είδη και επιτρέποντάς του να διατυπώσει τον «νόμο του ανταγωνιστικού αποκλεισμού». Ο νόμος ορίζει ότι μόνο ένα είδος μπορεί να υπάρχει σε μια οικολογική θέση. Στο σχ. 9.3. παρουσιάζονται τα αποτελέσματα των πειραμάτων του Gause για δύο είδη Parametium που καταλαμβάνουν την ίδια οικολογική θέση (Εικ. 9.3 α, β) και είδη που καταλαμβάνουν διαφορετικές οικολογικές κόγχες (Εικ. 9.3. γ).

Ρύζι. 9.3. ΕΝΑ- Καμπύλες αύξησης πληθυσμού δύο ειδών Parametium σε καλλιέργειες ενός είδους. ΜΑΥΡΟΙ ΚΥΚΛΟΙ - P Aurelia, λευκοί κύκλοι - P. Caudatum
σι- Καμπύλες ανάπτυξης P aurelia και P. Caudatum σε μια μικτή κουλτούρα.
By Gause, 1934
Το μοντέλο ανταγωνισμού (9.2) έχει ελλείψεις, συγκεκριμένα, προκύπτει ότι η συνύπαρξη δύο ειδών είναι δυνατή μόνο εάν η αφθονία τους περιορίζεται από διαφορετικούς παράγοντες, αλλά το μοντέλο δεν υποδεικνύει πόσο μεγάλες πρέπει να είναι οι διαφορές για να διασφαλιστεί η μακροπρόθεσμη συνύπαρξη . Ταυτόχρονα, είναι γνωστό ότι η μακροχρόνια συνύπαρξη σε ένα μεταβαλλόμενο περιβάλλον απαιτεί μια διαφορά που φτάνει σε μια ορισμένη τιμή. Η εισαγωγή στοχαστικών στοιχείων στο μοντέλο (για παράδειγμα, η εισαγωγή μιας συνάρτησης χρήσης πόρων) μας επιτρέπει να μελετήσουμε ποσοτικά αυτά τα ζητήματα.
Σύστημα αρπακτικών + θηραμάτων
 (9.7)
(9.7)
Εδώ, σε αντίθεση με το (9.2), τα ζώδια σι 12 Και σι 21 - διαφορετικό. Όπως και στην περίπτωση του ανταγωνισμού, η προέλευση
![]() (9.8)
(9.8)
είναι ένα μοναδικό σημείο τύπου ασταθούς κόμβου. Τρεις άλλες πιθανές στατικές καταστάσεις:
![]() ,(9.9)
,(9.9)
![]() (9.10)
(9.10)
![]() (9.11)
(9.11)
Έτσι είναι δυνατή μόνο το θήραμα (9.10), μόνο το αρπακτικό (9.9) (αν έχει άλλες πηγές τροφής) και η συνύπαρξη και των δύο ειδών (9.11). Η τελευταία επιλογή έχει ήδη εξεταστεί από εμάς στη διάλεξη 5. Πιθανοί τύποι πορτραίτων φάσης για το σύστημα αρπακτικών-θηραμάτων φαίνονται στην Εικ. 9.4.
Οι ισοκλίνες των οριζόντιων εφαπτομένων είναι ευθείες
Χ 2 = – σι 21 Χ 1 /ντο 2 + ένα 1/c2, Χ 2 = 0,
και τις ισοκλίνες των κατακόρυφων εφαπτομένων- ευθεία
Χ 2 = - ντο 1 Χ 1 /σι 12 + ένα 2 /σι 12 , Χ 1 = 0.
Τα ακίνητα σημεία βρίσκονται στην τομή των ισοκλινών της κάθετης και της οριζόντιας εφαπτομένης.

Από το σχ. 9.4 φαίνεται το εξής. σύστημα αρπακτικών-θηραμάτων (9.7) μπορεί να έχει μια σταθερή θέση ισορροπίας, στην οποίαο ρούμι ο πληθυσμός των θυμάτων έχει εξαφανιστεί τελείως ( ) και παρέμειναν μόνο αρπακτικά (κουκ 2 στο σχ. 9.4 ΕΝΑ). Προφανώς, μια τέτοια κατάσταση μπορεί να πραγματοποιηθεί μόνο εάν, εκτός από τον τύπο των θυμάτων που εξετάζουμε, Χ 1 αρπακτικό Χ 2 - έχει πρόσθετες πηγές ενέργειας. Αυτό το γεγονός αντικατοπτρίζεται στο μοντέλο από τον θετικό όρο στη δεξιά πλευρά της εξίσωσης για x 2 . Μοναδικά σημεία(1) και (3) (Εικ. 9.4 ΕΝΑ) είναι ασταθείς. Δεύτερη πιθανότητα – μια σταθερή ακίνητη κατάσταση στην οποία ο πληθυσμός των αρπακτικών έχει εξαφανιστεί εντελώς και έχουν απομείνει μόνο θύματα – σταθερό σημείο(3) (Εικ. 9.4 6 ). Εδώ είναι ένα ιδιαίτερο σημείο (1) – επίσης ένας ασταθής κόμβος.
Τέλος, η τρίτη πιθανότητα – σταθερή συνύπαρξη πληθυσμών αρπακτικών και θηραμάτων (Εικ. 9.4 V), των οποίων οι σταθερές αφθονίες εκφράζονται με τους τύπους (9.11).
Όπως και στην περίπτωση ενός μεμονωμένου πληθυσμού (βλ. Διάλεξη 3), για το μοντέλο (9.7) είναι δυνατό να αναπτυχθεί ένα στοχαστικό μοντέλο, αλλά δεν μπορεί να λυθεί ρητά. Επομένως, περιοριζόμαστε σε γενικές σκέψεις. Ας υποθέσουμε, για παράδειγμα, ότι το σημείο ισορροπίας βρίσκεται σε κάποια απόσταση από κάθε έναν από τους άξονες. Στη συνέχεια για τροχιές φάσης στις οποίες οι τιμέςΧ 1 , Χ 2 παραμένει αρκετά μεγάλο, ένα ντετερμινιστικό μοντέλο θα είναι αρκετά ικανοποιητικό. Αλλά αν σε κάποιο σημείο της τροχιάς φάσης κάποια μεταβλητή δεν είναι πολύ μεγάλη, τότε οι τυχαίες διακυμάνσεις μπορεί να γίνουν σημαντικές. Οδηγούν στο γεγονός ότι το αντιπροσωπευτικό σημείο θα μετακινηθεί σε έναν από τους άξονες, που σημαίνει την εξαφάνιση του αντίστοιχου είδους.
Έτσι, το στοχαστικό μοντέλο αποδεικνύεται ασταθές, αφού η στοχαστική «μετακίνηση» αργά ή γρήγορα οδηγεί στην εξαφάνιση ενός από τα είδη. Σε αυτό το είδος μοντέλου, το αρπακτικό τελικά πεθαίνει, είτε τυχαία είτε επειδή ο πληθυσμός του θηράματος εξαλείφεται πρώτα. Το στοχαστικό μοντέλο του συστήματος αρπακτικών-θηραμάτων εξηγεί καλά τα πειράματα του Gause (Gause, 1934), στα οποία βλεφαρίδες Paramettum candatumχρησίμευε ως θήραμα για ένα άλλο βλεφαροφόρο Didinium nasatum – αρπακτικό. Αναμένεται σύμφωνα με ντετερμινιστικές εξισώσεις (9.7) Οι αριθμοί ισορροπίας σε αυτά τα πειράματα ήταν περίπου μόνο πέντε άτομα από κάθε είδος, επομένως δεν υπάρχει τίποτα περίεργο στο γεγονός ότι σε κάθε επαναλαμβανόμενο πείραμα, είτε τα αρπακτικά είτε τα θηράματα (και μετά τα αρπακτικά) εξαφανίστηκαν αρκετά γρήγορα. Τα αποτελέσματα των πειραμάτων παρουσιάζονται στο Σχ. 9.5.

Ρύζι. 9.5. Υψος Parametium caudatum και αρπακτικά βλεφαροειδή Dadinium nasutum. Από : Gause G.F. Ο αγώνας για ύπαρξη. Βαλτιμόρη, 1934
Έτσι, η ανάλυση των μοντέλων Volterra αλληλεπίδρασης ειδών δείχνει ότι, παρά τη μεγάλη ποικιλία των τύπων συμπεριφοράς τέτοιων συστημάτων, δεν μπορούν να υπάρξουν καθόλου αμετάβλητες πληθυσμιακές διακυμάνσεις στο μοντέλο των ανταγωνιστικών ειδών. Ωστόσο, τέτοιες διακυμάνσεις παρατηρούνται στη φύση και στο πείραμα. Η ανάγκη για τη θεωρητική τους εξήγηση ήταν ένας από τους λόγους για τη διατύπωση των περιγραφών μοντέλων σε μια γενικότερη μορφή.
Γενικευμένα μοντέλα αλληλεπίδρασης δύο τύπων
Έχει προταθεί ένας μεγάλος αριθμός μοντέλων που περιγράφουν την αλληλεπίδραση ειδών, οι δεξιές πλευρές των εξισώσεων των οποίων ήταν συναρτήσεις των μεγεθών των πληθυσμών που αλληλεπιδρούν. Εξετάστηκε το ζήτημα της ανάπτυξης γενικών κριτηρίων για τον προσδιορισμό του τύπου των συναρτήσεων που μπορούν να περιγράψουν τη συμπεριφορά του προσωρινού μεγέθους πληθυσμού, συμπεριλαμβανομένων των σταθερών διακυμάνσεων. Τα πιο γνωστά από αυτά τα μοντέλα είναι αυτά των Kolmogorov (1935, αναθεωρημένη 1972) και Rosenzweig (1963).
 (9.12)
(9.12)
Το μοντέλο βασίζεται στις ακόλουθες παραδοχές:
1) Τα αρπακτικά δεν αλληλεπιδρούν μεταξύ τους, δηλ. ρυθμός αναπαραγωγής αρπακτικών κ 2 και αριθμός θυμάτων μεγάλο, που εξοντώνεται ανά μονάδα χρόνου από ένα αρπακτικό, δεν εξαρτάται από y.
2) Η αύξηση του αριθμού των θηραμάτων παρουσία αρπακτικών ισούται με την αύξηση στην απουσία αρπακτικών μείον τον αριθμό των θηραμάτων που εξοντώθηκαν από τα αρπακτικά. Λειτουργίες κ 1 (Χ), κ 2 (Χ), μεγάλο(Χ), είναι συνεχείς και ορίζονται στον θετικό ημιάξονα Χ, y³ 0.
3) dk 1 /dx< 0. Αυτό σημαίνει ότι ο συντελεστής πολλαπλασιασμού του θηράματος απουσία θηρευτή μειώνεται μονότονα με την αύξηση του αριθμού των θηραμάτων, γεγονός που αντανακλά την περιορισμένη τροφή και άλλους πόρους.
4) dk 2 /dx> 0, κ 2 (0) < 0 < k 2 (¥ ). Με την αύξηση του αριθμού των θηραμάτων, ο συντελεστής αναπαραγωγής των αρπακτικών μειώνεται μονότονα με την αύξηση του αριθμού των θηραμάτων, περνώντας από αρνητικές τιμές, (όταν δεν υπάρχει τίποτα να φάμε) στο θετικό.
5) Ο αριθμός των θυμάτων που εξοντώθηκαν από ένα αρπακτικό ανά μονάδα χρόνου μεγάλο(Χ)> 0 στο Ν> 0; μεγάλο(0)=0.
Πιθανοί τύποι πορτρέτων φάσης του συστήματος (9.12) φαίνονται στην εικ. 9.6:

Ρύζι. 9.6.Πορτραίτα φάσης του συστήματος Kolmogorov (9.12), το οποίο περιγράφει την αλληλεπίδραση δύο τύπων για διαφορετικές αναλογίες παραμέτρων. Επεξηγήσεις στο κείμενο.
Οι σταθερές λύσεις (υπάρχουν δύο ή τρεις από αυτές) έχουν τις ακόλουθες συντεταγμένες:
(1). ` x=0;` y=0.
Η αρχή των συντεταγμένων για οποιεσδήποτε τιμές των παραμέτρων είναι μια σέλα (Εικ. 9.6 α-δ).
(2). ` x=A,` y=0.(9.13)
ΕΝΑκαθορίζεται από την εξίσωση:
κ 1 (ΕΝΑ)=0.
Ακίνητος λύση (9.13) είναι μια σέλα αν σι< ΕΝΑ (Εικ. 9.6 ΕΝΑ, σι, σολ), σι καθορίζεται από την εξίσωση
κ 2 (σι)=0
Το σημείο (9.13) τοποθετείται στο θετικό τεταρτημόριο αν Β>Α . Αυτός είναι ένας σταθερός κόμπος .
Η τελευταία περίπτωση, που αντιστοιχεί στον θάνατο του αρπακτικού και την επιβίωση του θηράματος, φαίνεται στο Σχ. 9.6 V.
(3). ` x=B,` y=C.(9.14)
Η τιμή του C προσδιορίζεται από τις εξισώσεις:
Σημείο (9.14) - εστίαση (Εικ. 9.6 ΕΝΑ) ή κόμπο (Εικ. 9.6 σολ), η σταθερότητα του οποίου εξαρτάται από το πρόσημο της ποσότηταςμικρό
μικρό 2 = – κ 1 (Β)-κ 1 (σι)Β+Λ(σι)ΝΤΟ.
Αν μικρό>0, το σημείο είναι σταθερό ανμικρό<0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 σι)
Στην ξένη βιβλιογραφία, ένα παρόμοιο μοντέλο που προτείνεται από τους Rosenzweig και MacArthur (1963) θεωρείται συχνότερα:
 (9.15)
(9.15)
Οπου φά(Χ) - ο ρυθμός μεταβολής του αριθμού των θυμάτων Χαπουσία αρπακτικών, F( x,y) είναι η ένταση της θήρευσης, κ- συντελεστής που χαρακτηρίζει την αποτελεσματικότητα της μετατροπής της βιομάζας του θηράματος σε βιομάζα αρπακτικών, μι- Θνησιμότητα αρπακτικών.
Το μοντέλο (9.15) ανάγεται σε μια συγκεκριμένη περίπτωση του μοντέλου του Kolmogorov (9.12) υπό τις ακόλουθες παραδοχές:
1) ο αριθμός των αρπακτικών περιορίζεται μόνο από τον αριθμό των θηραμάτων,
2) ο ρυθμός με τον οποίο ένα δεδομένο άτομο ενός αρπακτικού τρώει ένα θήραμα εξαρτάται μόνο από την πυκνότητα του πληθυσμού του θηράματος και δεν εξαρτάται από την πυκνότητα του πληθυσμού των θηρευτών.
Τότε οι εξισώσεις (9.15) παίρνουν τη μορφή.

Κατά την περιγραφή της αλληλεπίδρασης πραγματικών ειδών, τα σωστά μέρη των εξισώσεων συγκεκριμενοποιούνται σύμφωνα με ιδέες για βιολογικές πραγματικότητες. Εξετάστε ένα από τα πιο δημοφιλή μοντέλα αυτού του τύπου.
Μοντέλο αλληλεπίδρασης μεταξύ δύο ειδών εντόμων (MacArthur, 1971)
Το μοντέλο, το οποίο θα συζητήσουμε παρακάτω, χρησιμοποιήθηκε για την επίλυση του πρακτικού προβλήματος του ελέγχου των παρασίτων με τη στείρωση των αρσενικών ενός από τα είδη. Με βάση τα βιολογικά χαρακτηριστικά της αλληλεπίδρασης των ειδών, γράφτηκε το παρακάτω μοντέλο
 (9.16)
(9.16)
Εδώ x,y- βιομάζα δύο ειδών εντόμων. Οι τροφικές αλληλεπιδράσεις των ειδών που περιγράφονται σε αυτό το μοντέλο είναι πολύ περίπλοκες. Αυτό καθορίζει τη μορφή των πολυωνύμων στη δεξιά πλευρά των εξισώσεων.
Θεωρήστε τη δεξιά πλευρά της πρώτης εξίσωσης. Είδη εντόμων Χτρώνε τις προνύμφες του είδους στο(μέλος + κ 3 y),αλλά ενήλικες του είδους στοτρώνε τις προνύμφες του είδους Χυπόκειται σε μεγάλο αριθμό ειδών Χή στοή και των δύο ειδών (μέλη -κ 4 xy, – y 2). Στο μικρό Χθνησιμότητα ειδών Χυψηλότερη από τη φυσική της αύξηση (1 -κ 1 +κ 2 x–x 2 < 0 στο μικρό Χ).Στη δεύτερη εξίσωση, ο όρος κ 5 αντανακλά τη φυσική ανάπτυξη του είδους y; -κ 6 y-αυτοσυγκράτηση αυτού του είδους,-κ 7 Χ- τρώγοντας προνύμφες του είδους στοέντομα του είδους x, k 8 xy – ανάπτυξη βιομάζας ειδών στοτρώγονται από ενήλικα έντομα του είδους στοπρονύμφες του είδους Χ.
Στο σχ. 9.7 παρουσιάζεται ο οριακός κύκλος, ο οποίος είναι η τροχιά μιας σταθερής περιοδικής λύσης του συστήματος (9.16).

Η λύση του ζητήματος του πώς να εξασφαλιστεί η συνύπαρξη ενός πληθυσμού με το βιολογικό του περιβάλλον, φυσικά, δεν μπορεί να επιτευχθεί χωρίς να ληφθούν υπόψη οι ιδιαιτερότητες ενός συγκεκριμένου βιολογικού συστήματος και η ανάλυση όλων των αλληλεπιδράσεων του. Ταυτόχρονα, η μελέτη επίσημων μαθηματικών μοντέλων καθιστά δυνατή την απάντηση σε ορισμένες γενικές ερωτήσεις. Μπορεί να υποστηριχθεί ότι για μοντέλα του τύπου (9.12), το γεγονός της συμβατότητας ή ασυμβατότητας των πληθυσμών δεν εξαρτάται από το αρχικό τους μέγεθος, αλλά καθορίζεται μόνο από τη φύση της αλληλεπίδρασης των ειδών. Το μοντέλο βοηθά στην απάντηση στο ερώτημα: πώς να επηρεάσετε τη βιοκένωση, να τη διαχειριστείτε ώστε να καταστρέψετε τα επιβλαβή είδη όσο το δυνατόν γρηγορότερα.
Η διαχείριση μπορεί να περιοριστεί σε μια βραχυπρόθεσμη, σπασμωδική αλλαγή στο μέγεθος του πληθυσμού ΧΚαι y.Αυτή η μέθοδος αντιστοιχεί σε μεθόδους ελέγχου, όπως η μεμονωμένη καταστροφή ενός ή και των δύο πληθυσμών με χημικά μέσα. Από τη δήλωση που διατυπώθηκε παραπάνω, μπορεί να φανεί ότι για συμβατούς πληθυσμούς αυτή η μέθοδος ελέγχου θα είναι αναποτελεσματική, καθώς με την πάροδο του χρόνου το σύστημα θα φτάσει ξανά σε ένα σταθερό καθεστώς.
Ένας άλλος τρόπος είναι να αλλάξετε τον τύπο των συναρτήσεων αλληλεπίδρασης μεταξύ των τύπων, για παράδειγμα, όταν αλλάζετε τις τιμές των παραμέτρων του συστήματος. Σε αυτήν ακριβώς την παραμετρική μέθοδο αντιστοιχούν οι βιολογικές μέθοδοι αγώνα. Έτσι, όταν εισάγονται στειρωμένα αρσενικά, ο συντελεστής φυσικής αύξησης του πληθυσμού μειώνεται. Εάν ταυτόχρονα λάβουμε έναν άλλο τύπο πορτραίτου φάσης, όπου υπάρχει μόνο μια σταθερή στατική κατάσταση με μηδενικούς αριθμούς παρασίτων, ο έλεγχος θα οδηγήσει στο επιθυμητό αποτέλεσμα – καταστροφή του πληθυσμού των παρασίτων. Είναι ενδιαφέρον να σημειωθεί ότι μερικές φορές είναι σκόπιμο να εφαρμοστεί η επίδραση όχι στο ίδιο το παράσιτο, αλλά στον σύντροφό του. Ποια από τις μεθόδους είναι πιο αποτελεσματική, στη γενική περίπτωση, είναι αδύνατο να πούμε. Εξαρτάται από τους διαθέσιμους ελέγχους και από τη ρητή μορφή των συναρτήσεων που περιγράφουν την αλληλεπίδραση των πληθυσμών.
Μοντέλο A.D.Bazykin
Η θεωρητική ανάλυση των μοντέλων αλληλεπίδρασης ειδών πραγματοποιείται με τον πιο εξαντλητικό τρόπο στο βιβλίο του A.D. Bazykin «Biophysics of interacting πληθυσμών» (M., Nauka, 1985).
Εξετάστε ένα από τα μοντέλα αρπακτικών-θηραμάτων που μελετήθηκαν σε αυτό το βιβλίο.
 (9.17)
(9.17)
Το σύστημα (9.17) είναι μια γενίκευση του απλούστερου μοντέλου αρπακτικών-θηραμάτων Volterra (5.17) λαμβάνοντας υπόψη την επίδραση κορεσμού των αρπακτικών. Το μοντέλο (5.17) υποθέτει ότι η ένταση της βόσκησης των θηραμάτων αυξάνεται γραμμικά με την αύξηση της πυκνότητας των θηραμάτων, η οποία δεν αντιστοιχεί στην πραγματικότητα σε υψηλές πυκνότητες θηραμάτων. Μπορούν να επιλεγούν διαφορετικές λειτουργίες για να περιγράψουν την εξάρτηση της διατροφής των αρπακτικών από την πυκνότητα του θηράματος. Είναι πολύ σημαντικό το επιλεγμένο να λειτουργεί με αύξηση Χτείνει ασυμπτωτικά σε σταθερή τιμή. Το μοντέλο (9.6) χρησιμοποίησε την λογιστική εξάρτηση. Στο μοντέλο Bazykin, η υπερβολή επιλέγεται ως συνάρτηση Χ/(1+px). Θυμηθείτε ότι ο τύπος του Monod, ο οποίος περιγράφει την εξάρτηση του ρυθμού ανάπτυξης των μικροοργανισμών από τη συγκέντρωση του υποστρώματος, έχει αυτή τη μορφή. Εδώ, το θήραμα δρα ως υπόστρωμα και το αρπακτικό ως μικροοργανισμοί. .
Το σύστημα (9.17) εξαρτάται από επτά παραμέτρους. Ο αριθμός των παραμέτρων μπορεί να μειωθεί αλλάζοντας τις μεταβλητές:
Χ® (ΕΝΑ Δ)Χ; y ® (ΕΝΑ Δ)/y;
t® (1/Α)t; g (9,18)
και εξαρτάται από τέσσερις παραμέτρους.
Για μια πλήρη ποιοτική μελέτη, είναι απαραίτητο να διαιρεθεί ο τετραδιάστατος χώρος παραμέτρων σε περιοχές με διαφορετικούς τύπους δυναμικής συμπεριφοράς, π.χ. κατασκευάστε ένα παραμετρικό ή δομικό πορτρέτο του συστήματος.
Στη συνέχεια, είναι απαραίτητο να κατασκευαστούν πορτρέτα φάσης για κάθε μία από τις περιοχές του παραμετρικού πορτρέτου και να περιγραφούν οι διακλαδώσεις που συμβαίνουν με τα πορτρέτα φάσης στα όρια διαφορετικών περιοχών του παραμετρικού πορτρέτου.
Η κατασκευή ενός πλήρους παραμετρικού πορτρέτου πραγματοποιείται με τη μορφή ενός συνόλου «φέτες» (προβολές) ενός παραμετρικού πορτρέτου μικρής διάστασης με σταθερές τιμές ορισμένων από τις παραμέτρους.
Παραμετρικό πορτρέτο του συστήματος (9.18) για σταθερό σολκαι μικρά μιφαίνεται στο σχήμα 9.8. Το πορτρέτο περιέχει 10 περιοχές με διαφορετικούς τύπους συμπεριφοράς τροχιάς φάσης.

Ρύζι. 9.8.Παραμετρικό πορτρέτο του συστήματος (9.18) για σταθερόσολ
και μικρά μι
Η συμπεριφορά του συστήματος με διαφορετικές αναλογίες παραμέτρων μπορεί να είναι σημαντικά διαφορετική (Εικ. 9.9). Στο σύστημα είναι δυνατά τα εξής:
1) μία σταθερή ισορροπία (περιοχές 1 και 5).
2) ένας σταθερός οριακός κύκλος (περιοχές 3 και 8).
3) δύο σταθερές ισορροπίες (περιοχή 2)
4) σταθερός οριακός κύκλος και ασταθής ισορροπία στο εσωτερικό του (περιοχές 6, 7, 9, 10)
5) σταθερός οριακός κύκλος και σταθερή ισορροπία εκτός αυτού (περιοχή 4).
Στις παραμετρικές περιοχές 7, 9, 10, η περιοχή έλξης ισορροπίας περιορίζεται από έναν ασταθή οριακό κύκλο που βρίσκεται μέσα στη σταθερή. Το πιο ενδιαφέρον είναι το πορτρέτο φάσης που αντιστοιχεί στην περιοχή 6 στο παραμετρικό πορτρέτο. Αναλυτικά φαίνεται στο Σχ. 9.10.

Η περιοχή έλξης της ισορροπίας Β 2 (σκιασμένη) είναι ένα «σαλιγκάρι» που στρίβει από την ασταθή εστία Β 1 . Εάν είναι γνωστό ότι την αρχική χρονική στιγμή το σύστημα βρισκόταν κοντά στο Β 1, τότε είναι δυνατό να κριθεί αν η αντίστοιχη τροχιά θα έρθει στην ισορροπία Β 2 ή σε έναν σταθερό οριακό κύκλο που περιβάλλει τα τρία σημεία ισορροπίας C ( σέλα), B 1 και B 2 μόνο με βάση πιθανολογικές εκτιμήσεις.

Εικ.9.10.Πορτραίτο φάσης του συστήματος 9.18 για την παραμετρική περιοχή 6. Η περιοχή έλξης Β 2 είναι σκιασμένη
Σε παραμετρικό πορτρέτο(9.7) υπάρχουν 22 διάφορα όρια διακλάδωσης που σχηματίζονται 7 διαφορετικών τύπων διακλαδώσεων. Η μελέτη τους καθιστά δυνατό τον εντοπισμό πιθανών τύπων συμπεριφοράς του συστήματος όταν αλλάζουν οι παράμετροί του. Για παράδειγμα, όταν μετακινείστε από την περιοχή 1 στην περιοχή 3 υπάρχει μια γέννηση ενός μικρού οριακού κύκλου ή μια ήπια γέννηση αυτοταλαντώσεων γύρω από μια ενιαία ισορροπία ΣΕ.Μια παρόμοια ήπια γέννηση αυτοταλαντώσεων, αλλά γύρω από μια από τις ισορροπίες, δηλαδή σι 1 , συμβαίνει κατά τη διέλευση των συνόρων περιοχών 2 και 4. Όταν μετακινείστε από την περιοχή 4 στην περιοχή 5 σταθερό οριακό κύκλο γύρω από ένα σημείοσι 1 "εκρήγνυται" στον βρόχο separatrix και το μόνο ελκυστικό σημείο είναι η ισορροπία σι 2 και τα λοιπά.
Ιδιαίτερο ενδιαφέρον για την πρακτική είναι, φυσικά, η ανάπτυξη κριτηρίων για την εγγύτητα ενός συστήματος στα όρια διακλάδωσης. Πράγματι, οι βιολόγοι γνωρίζουν καλά την ιδιότητα «ρυθμιστή» ή «ευελιξίας» των φυσικών οικολογικών συστημάτων. Αυτοί οι όροι συνήθως υποδηλώνουν την ικανότητα του συστήματος να απορροφά εξωτερικές επιρροές, όπως λέγαμε. Εφόσον η ένταση της εξωτερικής δράσης δεν υπερβαίνει μια ορισμένη κρίσιμη τιμή, η συμπεριφορά του συστήματος δεν υφίσταται ποιοτικές αλλαγές. Στο επίπεδο φάσης, αυτό αντιστοιχεί στην επιστροφή του συστήματος σε μια σταθερή κατάσταση ισορροπίας ή σε έναν σταθερό οριακό κύκλο, οι παράμετροι του οποίου δεν διαφέρουν πολύ από τον αρχικό. Όταν η ένταση της πρόσκρουσης υπερβαίνει την επιτρεπόμενη, το σύστημα «καταστρέφεται», περνά σε έναν ποιοτικά διαφορετικό τρόπο δυναμικής συμπεριφοράς, για παράδειγμα, απλώς σβήνει. Αυτό το φαινόμενο αντιστοιχεί σε μια μετάβαση διακλάδωσης.
Κάθε τύπος μετάβασης διακλάδωσης έχει τα δικά του διακριτικά χαρακτηριστικά που καθιστούν δυνατό να κριθεί ο κίνδυνος μιας τέτοιας μετάβασης για το οικοσύστημα. Ακολουθούν ορισμένα γενικά κριτήρια που μαρτυρούν την εγγύτητα ενός επικίνδυνου ορίου. Όπως στην περίπτωση ενός είδους, εάν η μείωση του αριθμού ενός από τα είδη κάνει το σύστημα να «κολλήσει» κοντά σε ένα ασταθές σημείο σέλας, το οποίο εκφράζεται σε πολύ αργή ανάκτηση του αριθμού στην αρχική τιμή, τότε το σύστημα βρίσκεται κοντά στο κρίσιμο όριο. Η αλλαγή στη μορφή των διακυμάνσεων στον αριθμό των αρπακτικών και των θηραμάτων χρησιμεύει επίσης ως δείκτης κινδύνου. Εάν οι ταλαντώσεις γίνουν χαλαρωτικές από σχεδόν αρμονικές και το πλάτος των ταλαντώσεων αυξηθεί, αυτό μπορεί να οδηγήσει σε απώλεια της σταθερότητας του συστήματος και την εξαφάνιση ενός από τα είδη.
Η περαιτέρω εμβάθυνση της μαθηματικής θεωρίας της αλληλεπίδρασης των ειδών ακολουθεί τη γραμμή λεπτομερειών της δομής των ίδιων των πληθυσμών και λαμβάνοντας υπόψη χρονικούς και χωρικούς παράγοντες.
Βιβλιογραφία.
Kolmogorov A.N. Ποιοτική μελέτη μαθηματικών μοντέλων πληθυσμιακής δυναμικής. // Προβλήματα κυβερνητικής. Μ., 1972, τεύχος 5.
MacArtur R. Graphical analysis of ecological systems// Division of biology report Perinceton University. 1971
AD Bazykin «Βιοφυσική αλληλεπιδρώντων πληθυσμών». Μ., Ναούκα, 1985.
W. Volterra: «Μαθηματική θεωρία του αγώνα για ύπαρξη». Μ.. Επιστήμη, 1976
Γάζες G.F. Ο αγώνας για ύπαρξη. Βαλτιμόρη, 1934.
ΜΟΝΤΕΛΟ ΥΠΟΛΟΓΙΣΤΗ "PREDATOR-Prey"
Kazachkov Igor Alekseevich 1 , Guseva Elena Nikolaevna 2
1 Κρατικό Τεχνικό Πανεπιστήμιο Magnitogorsk με το όνομα V.I. Γ.Ι. Nosova, Ινστιτούτο Κατασκευών, Αρχιτεκτονικής και Τέχνης, 5η φοιτήτρια
β Κρατικό Τεχνικό Πανεπιστήμιο Magnitogorsk Γ.Ι. Nosova, Ινστιτούτο Ενέργειας και Αυτοματοποιημένων Συστημάτων, Υποψήφια Παιδαγωγικών Επιστημών, Αναπληρωτής Καθηγητής του Τμήματος Επιχειρηματικής Πληροφορικής και Τεχνολογιών Πληροφορικής
σχόλιο
Αυτό το άρθρο είναι αφιερωμένο στην ανασκόπηση του μοντέλου υπολογιστή "αρπακτικό-θηράμα". Η μελέτη μας επιτρέπει να δηλώσουμε ότι η οικολογική μοντελοποίηση παίζει τεράστιο ρόλο στη μελέτη του περιβάλλοντος. Το θέμα αυτό είναι πολύπλευρο.
ΜΟΝΤΕΛΟ ΥΠΟΛΟΓΙΣΤΗ "PREDATOR-VICTIM"
Kazatchkov Igor Alekseevich 1, Guseva Elena Nikolaevna 2
1 Κρατικό Τεχνικό Πανεπιστήμιο Nosov Magnitogorsk, Ινστιτούτο Πολιτικών Μηχανικών, Αρχιτεκτονικής και Τεχνών, φοιτητής του 5ου μαθήματος
2 Κρατικό Τεχνικό Πανεπιστήμιο Nosov Magnitogorsk, Ινστιτούτο Ηλεκτρομηχανικής και Αυτοματοποιημένων Συστημάτων, Διδακτορικό στην Παιδαγωγική Επιστήμη, Αναπληρωτής Καθηγητής του Τμήματος Επιστήμης Υπολογιστών Επιχειρήσεων και Τεχνολογιών Πληροφορικής
Αφηρημένη
Αυτό το άρθρο παρέχει μια επισκόπηση του μοντέλου υπολογιστή "αρπακτικό-θύμα". Η μελέτη υποδηλώνει ότι η περιβαλλοντική προσομοίωση παίζει τεράστιο ρόλο στη μελέτη του περιβάλλοντος. Αυτό το πρόβλημα είναι πολύπλευρο.
Η οικολογική μοντελοποίηση χρησιμοποιείται για τη μελέτη του περιβάλλοντος γύρω μας. Τα μαθηματικά μοντέλα χρησιμοποιούνται σε περιπτώσεις όπου δεν υπάρχει φυσικό περιβάλλον και φυσικά αντικείμενα· βοηθά στην πρόβλεψη της επίδρασης διαφόρων παραγόντων στο αντικείμενο που μελετάται. Αυτή η μέθοδος αναλαμβάνει τις λειτουργίες ελέγχου, κατασκευής και ερμηνείας των αποτελεσμάτων. Με βάση τέτοιες μορφές, η οικολογική μοντελοποίηση ασχολείται με την αξιολόγηση των αλλαγών στο περιβάλλον γύρω μας.
Αυτή τη στιγμή, τέτοιες φόρμες χρησιμοποιούνται για τη μελέτη του περιβάλλοντος γύρω μας και όταν απαιτείται να μελετηθεί κάποια περιοχή του, τότε χρησιμοποιείται μαθηματική μοντελοποίηση. Αυτό το μοντέλο καθιστά δυνατή την πρόβλεψη της επίδρασης ορισμένων παραγόντων στο αντικείμενο μελέτης. Κάποτε, ο τύπος «αρπακτικό-θήραμα» προτάθηκε από επιστήμονες όπως: T. Malthus (Malthus 1798, Malthus 1905), Verhulst (Verhulst 1838), Pearl (Pearl 1927, 1930), καθώς και ο A. Lotka ( Lotka 1925, 1927 ) και V. Volterra (Volterra 1926) Αυτά τα μοντέλα αναπαράγουν το περιοδικό καθεστώς ταλάντωσης που εμφανίζεται ως αποτέλεσμα των αλληλεπιδράσεων μεταξύ των ειδών στη φύση.
Μία από τις κύριες μεθόδους γνωστικής γνώσης είναι η μοντελοποίηση. Εκτός από τη δυνατότητα πρόβλεψης των αλλαγών σε περιβάλλονβοηθά επίσης στην εύρεση του καλύτερου τρόπου επίλυσης του προβλήματος. Για μεγάλο χρονικό διάστημα, τα μαθηματικά μοντέλα έχουν χρησιμοποιηθεί στην οικολογία προκειμένου να καθιερωθούν πρότυπα, τάσεις στην ανάπτυξη των πληθυσμών και να βοηθήσουν στην ανάδειξη της ουσίας των παρατηρήσεων. Η διάταξη μπορεί να χρησιμεύσει ως δείγμα συμπεριφορά, αντικείμενο.
Κατά την αναδημιουργία αντικειμένων στη μαθηματική βιολογία, χρησιμοποιούνται προβλέψεις διαφόρων συστημάτων, παρέχονται ειδικές ατομικότητες βιοσυστημάτων: η εσωτερική δομή ενός ατόμου, συνθήκες υποστήριξης της ζωής, η σταθερότητα των οικολογικών συστημάτων, χάρη στα οποία σώζεται η ζωτική δραστηριότητα των συστημάτων.
Η έλευση της προσομοίωσης υπολογιστή έχει ωθήσει πολύ τα όρια της ερευνητικής ικανότητας. Υπήρχε η δυνατότητα πολυμερούς εφαρμογής δύσκολων μορφών που δεν επιτρέπουν αναλυτική μελέτη, εμφανίστηκαν νέες τάσεις, καθώς και προσομοίωση μοντελοποίησης.
Ας εξετάσουμε ποιο είναι το αντικείμενο της μοντελοποίησης. «Το αντικείμενο είναι ένας κλειστός βιότοπος όπου αλληλεπιδρούν δύο βιολογικοί πληθυσμοί: αρπακτικά και θήραμα. Συντελείται η διαδικασία της ανάπτυξης, της εξαφάνισης και της αναπαραγωγήςαπευθείας στην επιφάνεια του περιβάλλοντος. Τα θηράματα τρέφονται με τους πόρους που υπάρχουν στο περιβάλλον, ενώ τα αρπακτικά τρέφονται με θηράματα. Ταυτόχρονα, οι διατροφικοί πόροι μπορεί να είναι τόσο ανανεώσιμοι όσο και μη ανανεώσιμοι.
Το 1931, ο Vito Volterra εξήγαγε τους ακόλουθους νόμους της σχέσης θηρευτή-θηράματος.
Ο νόμος του περιοδικού κύκλου - η διαδικασία καταστροφής του θηράματος από ένα αρπακτικό συχνά οδηγεί σε περιοδικές διακυμάνσεις στον αριθμό των πληθυσμών και των δύο ειδών, ανάλογα μόνο με τον ρυθμό ανάπτυξης των σαρκοφάγων και φυτοφάγων και από την αρχική αναλογία του αριθμού τους .
Νόμος διατήρησης των μέσων όρων - η μέση αφθονία κάθε είδους είναι σταθερή, ανεξάρτητα από το αρχικό επίπεδο, με την προϋπόθεση ότι οι συγκεκριμένοι ρυθμοί αύξησης του πληθυσμού, καθώς και η αποτελεσματικότητα της θήρευσης, είναι σταθεροί.
Ο νόμος της παραβίασης των μέσων όρων - με μείωση και στα δύο είδη ανάλογα με τον αριθμό τους, ο μέσος πληθυσμός των θηραμάτων αυξάνεται και τα αρπακτικά - μειώνεται.
Το μοντέλο αρπακτικό-θήραμα είναι μια ειδική σχέση μεταξύ του αρπακτικού και του θηράματος, με αποτέλεσμα να ωφελούνται και τα δύο. Τα πιο υγιή και προσαρμοσμένα άτομα στις περιβαλλοντικές συνθήκες επιβιώνουν, δηλ. Όλα αυτά οφείλονται στη φυσική επιλογή. Σε ένα περιβάλλον όπου δεν υπάρχει δυνατότητα αναπαραγωγής, ο θηρευτής αργά ή γρήγορα θα καταστρέψει τον πληθυσμό των θηραμάτων, μετά τον οποίο θα πεθάνει ο ίδιος.
Υπάρχουν πολλοί ζωντανοί οργανισμοί στη γη, οι οποίοι, υπό ευνοϊκές συνθήκες, αυξάνουν τον αριθμό των συγγενών σε τεράστιες αναλογίες. Αυτή η ικανότητα ονομάζεται: βιοτικό δυναμικό του είδους, δηλ. αύξηση του πληθυσμού ενός είδους σε μια δεδομένη χρονική περίοδο. Κάθε είδος έχει το δικό του βιοτικό δυναμικό, για παράδειγμα, μεγάλα είδη οργανισμών μπορούν να αναπτυχθούν μόνο 1,1 φορές το χρόνο, ενώ οργανισμοί μικρότερων ειδών, όπως καρκινοειδή κ.λπ. μπορεί να αυξήσει την εμφάνισή τους έως και 1030 φορές, αλλά τα βακτήρια είναι ακόμη μεγαλύτερα. Σε οποιαδήποτε από αυτές τις περιπτώσεις, ο πληθυσμός θα αυξηθεί εκθετικά.
Η εκθετική αύξηση του πληθυσμού είναι μια γεωμετρική πρόοδος της αύξησης του πληθυσμού. Αυτή η ικανότητα μπορεί να παρατηρηθεί στο εργαστήριο σε βακτήρια, ζυμομύκητες. Σε μη εργαστηριακές συνθήκες, μπορεί να παρατηρηθεί εκθετική ανάπτυξη σε ακρίδες ή άλλα είδη εντόμων. Μια τέτοια αύξηση του αριθμού των ειδών μπορεί να παρατηρηθεί σε εκείνα τα μέρη όπου δεν έχει πρακτικά εχθρούς και υπάρχει περισσότερο από αρκετό φαγητό. Τελικά η ανάπτυξη του είδους, αφού ο πληθυσμός αυξήθηκε για μικρό χρονικό διάστημα, η πληθυσμιακή αύξηση άρχισε να μειώνεται.
Εξετάστε ένα μοντέλο υπολογιστή αναπαραγωγής θηλαστικών στο παράδειγμα του μοντέλου Lotka-Volterra. Αφήνω δύο είδη ζώων ζουν σε μια συγκεκριμένη περιοχή: ελάφια και λύκοι. Μαθηματικό μοντέλο μεταβολής πληθυσμού στο μοντέλοΔίσκοι-Volterra:
Ο αρχικός αριθμός των θυμάτων είναι xn, ο αριθμός των αρπακτικών είναι yn.
Παράμετροι μοντέλου:
P1 είναι η πιθανότητα συνάντησης με ένα αρπακτικό,
P2 είναι ο ρυθμός ανάπτυξης των αρπακτικών σε βάρος του θηράματος,
d είναι το ποσοστό θνησιμότητας των αρπακτικών,
α είναι η αύξηση του αριθμού των θυμάτων.
Στην εργασία εκπαίδευσης, ορίστηκαν οι ακόλουθες τιμές: ο αριθμός των ελαφιών ήταν 500, ο αριθμός των λύκων ήταν 10, ο ρυθμός ανάπτυξης των ελαφιών ήταν 0,02, ο ρυθμός ανάπτυξης των λύκων ήταν 0,1, η πιθανότητα να συναντήσετε ένα αρπακτικό ήταν 0,0026, ο ρυθμός αύξησης των αρπακτικών λόγω θηράματος ήταν 0,000056. Τα δεδομένα υπολογίζονται για 203 χρόνια.
Διερεύνηση επιρροής ο ρυθμός αύξησης των θυμάτων για την ανάπτυξη δύο πληθυσμών, οι υπόλοιπες παράμετροι θα μείνουν αμετάβλητες.Στο Σχήμα 1, παρατηρείται αύξηση του αριθμού των θηραμάτων και στη συνέχεια, με κάποια καθυστέρηση, παρατηρείται αύξηση των αρπακτικών. Τότε τα αρπακτικά βγάζουν νοκ άουτ το θήραμα, ο αριθμός των θηραμάτων πέφτει απότομα, ακολουθούμενος από τη μείωση του αριθμού των αρπακτικών (Εικ. 1).

Σχήμα 1. Μέγεθος πληθυσμού με χαμηλά ποσοστά γεννήσεων μεταξύ των θυμάτων
Ας αναλύσουμε την αλλαγή στο μοντέλο αυξάνοντας το ποσοστό γεννήσεων του θύματος a=0,06. Στο Σχήμα 2, βλέπουμε μια κυκλική ταλαντωτική διαδικασία που οδηγεί σε αύξηση του αριθμού και των δύο πληθυσμών με την πάροδο του χρόνου (Εικ. 2).

Σχήμα 2. Μέγεθος πληθυσμού στο μέσο ποσοστό γεννήσεων των θυμάτων
Ας εξετάσουμε πώς θα αλλάξει η δυναμική των πληθυσμών με υψηλή τιμή του ποσοστού γεννήσεων του θύματος a = 1,13. Στο σχ. 3, υπάρχει μια απότομη αύξηση στον αριθμό και των δύο πληθυσμών, ακολουθούμενη από εξαφάνιση τόσο του θηράματος όσο και του αρπακτικού. Αυτό οφείλεται στο γεγονός ότι ο πληθυσμός των θυμάτων έχει αυξηθεί σε τέτοιο βαθμό που οι πόροι έχουν αρχίσει να εξαντλούνται, με αποτέλεσμα το θύμα να πεθαίνει. Η εξαφάνιση των αρπακτικών οφείλεται στο γεγονός ότι ο αριθμός των θυμάτων έχει μειωθεί και τα αρπακτικά έχουν εξαντλήσει τους πόρους για την ύπαρξη τους.

Εικόνα 3. Πληθυσμοί με υψηλά ποσοστά γεννήσεων σε θήραμα
Με βάση την ανάλυση δεδομένων πειραμάτων υπολογιστή, μπορούμε να συμπεράνουμε ότι η μοντελοποίηση υπολογιστή μας επιτρέπει να προβλέψουμε το μέγεθος των πληθυσμών, να μελετήσουμε την επίδραση διαφόρων παραγόντων στη δυναμική του πληθυσμού. Στο παραπάνω παράδειγμα, διερευνήσαμε το μοντέλο θηρευτή-θηράματος, την επίδραση του ποσοστού γεννήσεων των θηραμάτων στον αριθμό των ελαφιών και των λύκων. Μια μικρή αύξηση του πληθυσμού των θηραμάτων οδηγεί σε μικρή αύξηση του θηράματος, το οποίο μετά από μια ορισμένη περίοδο καταστρέφεται από τα αρπακτικά.Μια μέτρια αύξηση του πληθυσμού των θηραμάτων οδηγεί σε αύξηση του μεγέθους και των δύο πληθυσμών. Μια υψηλή αύξηση του πληθυσμού των θηραμάτων οδηγεί πρώτα σε ταχεία αύξηση του πληθυσμού των θηραμάτων, αυτό επηρεάζει την αύξηση της ανάπτυξης των αρπακτικών, αλλά στη συνέχεια τα αρπακτικά αναπαραγωγής καταστρέφουν γρήγορα τον πληθυσμό των ελαφιών. Ως αποτέλεσμα, και τα δύο είδη εξαφανίζονται.
Τα αρπακτικά μπορούν να φάνε φυτοφάγα, αλλά και αδύναμα αρπακτικά. Τα αρπακτικά έχουν μεγάλη γκάμα τροφών, αλλάζουν εύκολα από το ένα θήραμα στο άλλο, πιο προσιτά. Τα αρπακτικά επιτίθενται συχνά στα αδύναμα θηράματα. Διατηρείται μια οικολογική ισορροπία μεταξύ των πληθυσμών θηραμάτων-αρπακτικών.[ ...]
Εάν η ισορροπία είναι ασταθής (δεν υπάρχουν οριακά κύκλοι) ή ο εξωτερικός κύκλος είναι ασταθής, τότε οι αριθμοί και των δύο ειδών, που παρουσιάζουν έντονες διακυμάνσεις, φεύγουν από την περιοχή της ισορροπίας. Επιπλέον, ο γρήγορος εκφυλισμός (στην πρώτη κατάσταση) συμβαίνει με χαμηλή προσαρμογή του αρπακτικού, δηλ. με την υψηλή θνησιμότητα του (σε σύγκριση με το ρυθμό αναπαραγωγής του θύματος). Αυτό σημαίνει ότι ένα αρπακτικό που είναι αδύναμο από όλες τις απόψεις δεν συμβάλλει στη σταθεροποίηση του συστήματος και πεθαίνει από μόνο του.[ ...]
Η πίεση των αρπακτικών είναι ιδιαίτερα ισχυρή όταν, στη συνεξέλιξη αρπακτικών-θηραμάτων, η ισορροπία μετατοπίζεται προς τον θηρευτή και το εύρος του θηράματος στενεύει. Ο αγώνας ανταγωνισμού σχετίζεται στενά με την έλλειψη πόρων τροφίμων, μπορεί επίσης να είναι ένας άμεσος αγώνας, για παράδειγμα, των αρπακτικών για το διάστημα ως πόρο, αλλά τις περισσότερες φορές είναι απλώς η μετατόπιση ενός είδους που δεν έχει αρκετή τροφή σε ένα δίνεται έδαφος από ένα είδος που έχει αρκετή από την ίδια ποσότητα τροφής. Αυτός είναι ανταγωνισμός μεταξύ των ειδών.[ ...]
 |
Τέλος, στο σύστημα «αρπακτικού-θηράματος» που περιγράφεται από το μοντέλο (2.7), η εμφάνιση αστάθειας διάχυσης (με σταθερότητα τοπικής ισορροπίας) είναι δυνατή μόνο εάν η φυσική θνησιμότητα του αρπακτικού αυξάνεται με τον πληθυσμό του ταχύτερα από τη γραμμική συνάρτηση. Η τροφική λειτουργία διαφέρει από τη Volterra ή όταν ο πληθυσμός των θηραμάτων είναι πληθυσμός τύπου Ollie.[ ...]
Θεωρητικά, στα μοντέλα "ένας θηρευτής - δύο θηράματα", η ισοδύναμη θήραμα (έλλειψη προτίμησης για τον ένα ή τον άλλο τύπο θηράματος) μπορεί να επηρεάσει την ανταγωνιστική συνύπαρξη ειδών θηράματος μόνο σε εκείνα τα μέρη όπου υπάρχει ήδη μια δυνητικά σταθερή ισορροπία. Η ποικιλότητα μπορεί να αυξηθεί μόνο υπό συνθήκες όπου τα είδη με μικρότερη ανταγωνιστικότητα έχουν υψηλότερο ρυθμό πληθυσμιακής αύξησης από τα κυρίαρχα είδη. Αυτό καθιστά δυνατή την κατανόηση της κατάστασης όταν ακόμη και η βόσκηση οδηγεί σε αύξηση της ποικιλότητας των φυτικών ειδών, όπου ένας μεγαλύτερος αριθμός ειδών που έχουν επιλεγεί για ταχεία αναπαραγωγή συνυπάρχουν με είδη των οποίων η εξέλιξη στοχεύει στην αύξηση της ανταγωνιστικότητας[ ...]
Με τον ίδιο τρόπο, η επιλογή του θηράματος, ανάλογα με την πυκνότητά του, μπορεί να οδηγήσει σε μια σταθερή ισορροπία σε θεωρητικά μοντέλα δύο ανταγωνιστικών τύπων θηράματος, όπου δεν υπήρχε ισορροπία πριν. Για να γίνει αυτό, ο θηρευτής θα πρέπει να είναι ικανός για λειτουργικές και αριθμητικές αποκρίσεις στις αλλαγές στην πυκνότητα του θηράματος. Είναι πιθανό, ωστόσο, η αλλαγή (δυσανάλογα συχνές επιθέσεις στο πιο άφθονο θύμα) να είναι πιο σημαντική σε αυτή την περίπτωση. Πράγματι, η μεταγωγή έχει βρεθεί ότι έχει σταθεροποιητικό αποτέλεσμα στα συστήματα «one predator - n prey» και είναι ο μόνος μηχανισμός ικανός να σταθεροποιεί τις αλληλεπιδράσεις σε περιπτώσεις όπου οι κόγχες του θηράματος επικαλύπτονται πλήρως. Αυτόν τον ρόλο μπορούν να παίξουν μη εξειδικευμένοι θηρευτές. Η προτίμηση των πιο εξειδικευμένων αρπακτικών για έναν κυρίαρχο ανταγωνιστή ενεργεί με τον ίδιο τρόπο όπως η εναλλαγή αρπακτικών και μπορεί να σταθεροποιήσει τις θεωρητικές αλληλεπιδράσεις σε μοντέλα στα οποία δεν υπήρχε ισορροπία μεταξύ των ειδών θηραμάτων πριν, υπό τον όρο ότι οι κόγχες τους είναι σε κάποιο βαθμό διαχωρισμένες.[ .. .]
Επίσης, η κοινότητα δεν είναι σταθεροποιημένη και το αρπακτικό είναι «δυνατό από κάθε άποψη», δηλ. καλά προσαρμοσμένο σε ένα δεδομένο θήραμα και με χαμηλή σχετική θνησιμότητα. Σε αυτή την περίπτωση, το σύστημα έχει έναν ασταθή οριακό κύκλο και, παρά τη σταθερότητα της θέσης ισορροπίας, εκφυλίζεται σε ένα τυχαίο περιβάλλον (ο θηρευτής τρώει το θήραμα και, ως αποτέλεσμα, πεθαίνει). Αυτή η κατάσταση αντιστοιχεί σε αργό εκφυλισμό.[ ...]
Έτσι, με μια καλή προσαρμογή ενός αρπακτικού κοντά σε μια σταθερή ισορροπία, μπορούν να προκύψουν ασταθείς και σταθεροί κύκλοι, δηλ. Ανάλογα με τις αρχικές συνθήκες, το σύστημα «αρπακτικού-θηράματος» είτε τείνει να ισορροπεί, είτε, ταλαντούμενο, το εγκαταλείπει, είτε σταθερές διακυμάνσεις στον αριθμό και των δύο ειδών δημιουργούνται κοντά στην ισορροπία[ ...]
Οι οργανισμοί που ταξινομούνται ως αρπακτικά τρέφονται με άλλους οργανισμούς, καταστρέφοντας τη λεία τους. Έτσι, μεταξύ των ζωντανών οργανισμών, θα πρέπει να διακρίνεται ένα ακόμη σύστημα ταξινόμησης, δηλαδή «αρπακτικά» και «θύματα». Οι σχέσεις μεταξύ τέτοιων οργανισμών έχουν εξελιχθεί σε όλη την εξέλιξη της ζωής στον πλανήτη μας. Οι αρπακτικοί οργανισμοί ενεργούν ως φυσικοί ρυθμιστές του αριθμού των θηραματικών οργανισμών. Η αύξηση του αριθμού των "αρπακτικών" οδηγεί σε μείωση του αριθμού των "θηραμάτων", η οποία, με τη σειρά της, μειώνει την προσφορά τροφής ("θηράματα") για τα "αρπακτικά", η οποία γενικά υπαγορεύει μείωση του αριθμού του «θηράματος» κλπ. Έτσι, στη βιοκένωση, υπάρχουν συνεχείς διακυμάνσεις στον αριθμό των αρπακτικών και των θηραμάτων, γενικά, μια ορισμένη ισορροπία εδραιώνεται για ορισμένο χρονικό διάστημα μέσα σε αρκετά σταθερές περιβαλλοντικές συνθήκες.[ ... ]
Αυτό τελικά καταλήγει σε μια οικολογική ισορροπία μεταξύ των πληθυσμών αρπακτικών και θηραμάτων.[ ...]
Για μια τροφική συνάρτηση του τρίτου τύπου, η κατάσταση ισορροπίας θα είναι σταθερή εάν όπου N είναι το σημείο καμπής της συνάρτησης (βλ. Εικ. 2, γ). Αυτό προκύπτει από το γεγονός ότι η τροφική συνάρτηση είναι κοίλη στο διάστημα και, κατά συνέπεια, αυξάνεται το σχετικό μερίδιο της κατανάλωσης θηράματος από το αρπακτικό.[ ...]
Έστω Гг = -Г, δηλ. υπάρχει μια κοινότητα του τύπου «αρπακτικό-θηράμα». Στην περίπτωση αυτή, ο πρώτος όρος στην έκφραση (7.4) είναι ίσος με μηδέν και για να πληρούται η συνθήκη της σταθερότητας ως προς την πιθανότητα της κατάστασης ισορροπίας Ν, απαιτείται ούτε ο δεύτερος όρος να είναι θετικός.[ ...]
Έτσι, για την εξεταζόμενη κοινότητα του τύπου θηρευτή-θηράματος, μπορούμε να συμπεράνουμε ότι η γενικά θετική ισορροπία είναι ασυμπτωτικά σταθερή, δηλ. για τυχόν αρχικά δεδομένα με την προϋπόθεση ότι N >0.[ ...]
Έτσι, σε ένα ομοιογενές περιβάλλον που δεν έχει καταφύγια για αναπαραγωγή, ένα αρπακτικό αργά ή γρήγορα καταστρέφει τον πληθυσμό των θηραμάτων και μετά πεθαίνει ο ίδιος. Waves of life» (αλλαγές στον αριθμό του αρπακτικού και του θηράματος) διαδέχονται το ένα το άλλο με σταθερή μετατόπιση φάσης και κατά μέσο όρο ο αριθμός τόσο του αρπακτικού όσο και του θηράματος παραμένει περίπου στο ίδιο επίπεδο. Η διάρκεια της περιόδου εξαρτάται από τους ρυθμούς ανάπτυξης και των δύο ειδών και από τις αρχικές παραμέτρους. Για τον πληθυσμό των θηραμάτων, η επιρροή του αρπακτικού είναι θετική, αφού η υπερβολική αναπαραγωγή του θα οδηγούσε σε κατάρρευση του αριθμού του. Με τη σειρά τους, όλοι οι μηχανισμοί που εμποδίζουν την πλήρη εξόντωση του θηράματος συμβάλλουν στη διατήρηση της τροφικής βάσης του αρπακτικού.[ ...]
Άλλες τροποποιήσεις μπορεί να οφείλονται στη συμπεριφορά του αρπακτικού. Ο αριθμός των ατόμων θηράματος που μπορεί να καταναλώσει το αρπακτικό Δοσμένος χρόνος, έχει τα όριά του. Η επίδραση του κορεσμού του αρπακτικού όταν πλησιάζει αυτό το όριο φαίνεται στον Πίνακα. 2-4, Β. Οι αλληλεπιδράσεις που περιγράφονται από τις εξισώσεις 5 και 6 μπορεί να έχουν σταθερά σημεία ισορροπίας ή να παρουσιάζουν κυκλικές διακυμάνσεις. Ωστόσο, τέτοιοι κύκλοι διαφέρουν από αυτούς που αντικατοπτρίζονται στις εξισώσεις Lotka-Volterra 1 και 2. Οι κύκλοι που μεταφέρονται από τις εξισώσεις 5 και 6 μπορεί να έχουν σταθερό πλάτος και μέσες πυκνότητες εφόσον το μέσο είναι σταθερό. μετά την παραβίαση, μπορούν να επιστρέψουν στα προηγούμενα πλάτη και μέσες πυκνότητες. Τέτοιοι κύκλοι, οι οποίοι αποκαθίστανται μετά από παραβιάσεις, ονομάζονται κύκλοι σταθερών ορίων. Η αλληλεπίδραση ενός λαγού και ενός λύγκα μπορεί να θεωρηθεί σταθερός οριακός κύκλος, αλλά αυτός δεν είναι κύκλος Lotka-Volterra[ ...]
Ας εξετάσουμε την εμφάνιση αστάθειας διάχυσης στο σύστημα "αρπακτικό-θηράμα", αλλά πρώτα γράφουμε τις συνθήκες που διασφαλίζουν την εμφάνιση αστάθειας διάχυσης στο σύστημα (1.1) σε n = 2. Είναι σαφές ότι η ισορροπία (Ν , W) είναι τοπικό (δηλαδή [ .. .]
Ας στραφούμε στην ερμηνεία περιπτώσεων που σχετίζονται με τη μακροχρόνια συνύπαρξη αρπακτικού και θηράματος. Είναι σαφές ότι απουσία οριακών κύκλων, μια σταθερή ισορροπία θα αντιστοιχεί σε διακυμάνσεις πληθυσμού σε ένα τυχαίο περιβάλλον και το πλάτος τους θα είναι ανάλογο με τη διασπορά των διαταραχών. Ένα τέτοιο φαινόμενο θα συμβεί εάν το αρπακτικό έχει υψηλή σχετική θνησιμότητα και ταυτόχρονα υψηλό βαθμό προσαρμογής σε ένα δεδομένο θήραμα[ ...]
Ας εξετάσουμε τώρα πώς αλλάζει η δυναμική του συστήματος με την αύξηση της ικανότητας του αρπακτικού, δηλ. με μείωση του b από 1 σε 0. Εάν η φυσική κατάσταση είναι αρκετά χαμηλή, τότε δεν υπάρχουν οριακά κύκλοι και η ισορροπία είναι ασταθής. Με την ανάπτυξη της φυσικής κατάστασης κοντά σε αυτή την ισορροπία, είναι δυνατή η εμφάνιση ενός σταθερού κύκλου και στη συνέχεια ενός εξωτερικού ασταθούς. Ανάλογα με τις αρχικές συνθήκες (την αναλογία της βιομάζας αρπακτικών και θηραμάτων), το σύστημα μπορεί είτε να χάσει τη σταθερότητα, δηλ. εγκαταλείψουν τη γειτονιά της ισορροπίας, ή θα δημιουργηθούν σταθερές ταλαντώσεις σε αυτήν με την πάροδο του χρόνου. Η περαιτέρω ανάπτυξη της φυσικής κατάστασης καθιστά αδύνατη την ταλαντευτική φύση της συμπεριφοράς του συστήματος. Ωστόσο, όταν β [...]
Ένα παράδειγμα αρνητικής (σταθεροποιητικής) ανάδρασης είναι η σχέση μεταξύ αρπακτικού και θηράματος ή η λειτουργία του ανθρακικού συστήματος των ωκεανών (διάλυμα CO2 στο νερό: CO2 + H2O -> H2CO3). Κανονικά, η ποσότητα του διοξειδίου του άνθρακα που διαλύεται στο νερό των ωκεανών βρίσκεται σε μερική ισορροπία με τη συγκέντρωση του διοξειδίου του άνθρακα στην ατμόσφαιρα. Οι τοπικές αυξήσεις του διοξειδίου του άνθρακα στην ατμόσφαιρα μετά από ηφαιστειακές εκρήξεις οδηγούν στην εντατικοποίηση της φωτοσύνθεσης και στην απορρόφησή της από το ανθρακικό σύστημα του ωκεανού. Καθώς το επίπεδο του διοξειδίου του άνθρακα στην ατμόσφαιρα μειώνεται, το ανθρακικό σύστημα των ωκεανών απελευθερώνει CO2 στην ατμόσφαιρα. Επομένως, η συγκέντρωση του διοξειδίου του άνθρακα στην ατμόσφαιρα είναι αρκετά σταθερή.[ ...]
[ ...]
Όπως σημειώνει ο R. Ricklefs (1979), υπάρχουν παράγοντες που συμβάλλουν στη σταθεροποίηση των σχέσεων στο σύστημα «αρπακτικού-θηράματος»: η αναποτελεσματικότητα του αρπακτικού, η παρουσία εναλλακτικών πόρων διατροφής στον θηρευτή, η μείωση της καθυστέρησης στο η αντίδραση του αρπακτικού, καθώς και οι περιβαλλοντικοί περιορισμοί που επιβάλλονται από το εξωτερικό περιβάλλον σε έναν ή περισσότερους διαφορετικούς πληθυσμούς. Οι αλληλεπιδράσεις μεταξύ των πληθυσμών αρπακτικών και θηραμάτων είναι πολύ διαφορετικές και πολύπλοκες. Έτσι, εάν τα αρπακτικά είναι αρκετά αποτελεσματικά, μπορούν να ρυθμίσουν την πυκνότητα του πληθυσμού των θηραμάτων, διατηρώντας τον σε επίπεδο κάτω από την ικανότητα του περιβάλλοντος. Μέσω της επιρροής που ασκούν στους πληθυσμούς των θηραμάτων, τα αρπακτικά επηρεάζουν την εξέλιξη διαφόρων χαρακτηριστικών θηραμάτων, γεγονός που οδηγεί τελικά σε μια οικολογική ισορροπία μεταξύ των πληθυσμών αρπακτικών και θηραμάτων[ ...]
Εάν πληρούται μία από τις προϋποθέσεις: 0 1/2. Εάν 6 > 1 (kA [ ...]
Η σταθερότητα του βιολογικού οργανισμού και του περιβάλλοντος εξαρτάται μόνο από την αλληλεπίδραση φυτών - αυτότροφων και φυτοφάγων ετερότροφων οργανισμών. Τα αρπακτικά οποιουδήποτε μεγέθους δεν είναι σε θέση να διαταράξουν την οικολογική ισορροπία της κοινότητας, αφού υπό φυσικές συνθήκες δεν μπορούν να αυξήσουν τον αριθμό τους με σταθερό αριθμό θηραμάτων. Τα αρπακτικά όχι μόνο πρέπει να κινούνται οι ίδιοι, αλλά μπορούν να τρέφονται μόνο με κινούμενα ζώα.[ ...]
Κανένα άλλο ψάρι δεν είναι τόσο ευρέως διαδεδομένο όσο οι λούτσοι. Στις λίγες περιοχές αλιείας σε λιμνάζοντα ή ρέοντα νερά, δεν υπάρχει πίεση από τους λούτσους για τη διατήρηση της ισορροπίας μεταξύ θηράματος και αρπακτικού. Η Pike εκπροσωπείται εξαιρετικά στον κόσμο. Πιάνονται σε όλο το βόρειο ημισφαίριο από τις Ηνωμένες Πολιτείες και τον Καναδά έως Βόρεια Αμερική, μέσω της Ευρώπης στη βόρεια Ασία.[ ...]
Μια άλλη δυνατότητα σταθερής συνύπαρξης προκύπτει εδώ, σε ένα στενό εύρος σχετικά υψηλής προσαρμογής. Κατά τη μετάβαση σε ένα ασταθές καθεστώς με ένα πολύ «καλό» αρπακτικό, μπορεί να προκύψει ένας σταθερός εξωτερικός περιοριστικός κύκλος, στον οποίο η διασπορά της βιομάζας εξισορροπείται από την εισροή της στο σύστημα (υψηλή παραγωγικότητα του θηράματος). Τότε προκύπτει μια περίεργη κατάσταση όταν οι πιο πιθανές είναι δύο χαρακτηριστικές τιμές του πλάτους των τυχαίων ταλαντώσεων. Μερικά συμβαίνουν κοντά στην ισορροπία, άλλα κοντά στον οριακό κύκλο και είναι πιθανές περισσότερο ή λιγότερο συχνές μεταβάσεις μεταξύ αυτών των τρόπων λειτουργίας.[ ...]
Υποθετικοί πληθυσμοί που συμπεριφέρονται σύμφωνα με τα διανύσματα στο Σχ. 10.11 A, φαίνεται στο σχ. 10.11,-Β με τη βοήθεια γραφήματος που δείχνει τη δυναμική της αναλογίας των αριθμών αρπακτικού και θηράματος και στο σχ. 10.11.5 με τη μορφή γραφήματος της δυναμικής του αριθμού των αρπακτικών και των θηραμάτων με την πάροδο του χρόνου. Στον πληθυσμό των θηραμάτων, καθώς μετακινείται από μια ισορροπία χαμηλής πυκνότητας σε μια ισορροπία υψηλής πυκνότητας και επιστρέφει πίσω, εμφανίζεται μια «λάμψη» αριθμών. Και αυτό το ξέσπασμα δεν είναι αποτέλεσμα μιας εξίσου έντονης αλλαγής στο περιβάλλον. Αντίθετα, αυτή η μεταβολή των αριθμών δημιουργείται από την ίδια την επίδραση (με χαμηλό επίπεδο «θορύβου» στο περιβάλλον) και, ειδικότερα, αντανακλά την ύπαρξη αρκετών καταστάσεων ισορροπίας. Παρόμοιος συλλογισμός μπορεί να χρησιμοποιηθεί για να εξηγηθούν πιο περίπλοκες περιπτώσεις πληθυσμιακής δυναμικής σε φυσικούς πληθυσμούς.[ ...]
Η πιο σημαντική ιδιότητα ενός οικοσυστήματος είναι η σταθερότητά του, η ισορροπία ανταλλαγής και οι διεργασίες που συμβαίνουν σε αυτό. Η ικανότητα των πληθυσμών ή των οικοσυστημάτων να διατηρούν μια σταθερή δυναμική ισορροπία στις μεταβαλλόμενες περιβαλλοντικές συνθήκες ονομάζεται ομοιόσταση (homoios - το ίδιο, παρόμοιο, στάση - κατάσταση). Η ομοιόσταση βασίζεται στην αρχή της ανατροφοδότησης. Για να διατηρηθεί η ισορροπία στη φύση, δεν απαιτείται εξωτερικός έλεγχος. Παράδειγμα ομοιόστασης είναι το υποσύστημα «αρπακτικό-θήραμα», στο οποίο ρυθμίζεται η πυκνότητα των πληθυσμών αρπακτικών και θηραμάτων.[ ...]
Ένα φυσικό οικοσύστημα (biogeocenosis) λειτουργεί σταθερά με τη συνεχή αλληλεπίδραση των στοιχείων του, την κυκλοφορία ουσιών, τη μεταφορά χημικής, ενέργειας, γενετικής και άλλης ενέργειας και πληροφοριών μέσω αλυσίδων-καναλιών. Σύμφωνα με την αρχή της ισορροπίας, κάθε φυσικό σύστημα με ροή ενέργειας και πληροφοριών που διέρχεται από αυτό τείνει να αναπτύξει μια σταθερή κατάσταση. Ταυτόχρονα, η σταθερότητα των οικοσυστημάτων παρέχεται αυτόματα λόγω του μηχανισμού ανάδρασης. Η ανατροφοδότηση συνίσταται στη χρήση των δεδομένων που λαμβάνονται από τα διαχειριζόμενα στοιχεία του οικοσυστήματος για την πραγματοποίηση προσαρμογών στα στοιχεία διαχείρισης στη διαδικασία. Η σχέση "αρπακτικό" - "θήραμα" που συζητήθηκε παραπάνω σε αυτό το πλαίσιο μπορεί να περιγραφεί κάπως πιο λεπτομερώς. έτσι, στο υδάτινο οικοσύστημα αρπακτικά ψάρια(λούτσος στη λίμνη) τρώνε άλλους τύπους ψαριών θηραμάτων (σταυροειδής κυπρίνος). εάν ο αριθμός του σταυροειδούς κυπρίνου αυξηθεί, αυτό είναι ένα παράδειγμα θετικής ανατροφοδότησης. ο λούτσος, που τρέφεται με σταυροειδείς κυπρίνους, μειώνει τους αριθμούς του - αυτό είναι ένα παράδειγμα αρνητικής ανατροφοδότησης. με την αύξηση του αριθμού των αρπακτικών, ο αριθμός των θυμάτων μειώνεται και το αρπακτικό, που στερείται τροφής, μειώνει επίσης την αύξηση του πληθυσμού του. στο τέλος, στην υπό εξέταση λίμνη, δημιουργείται μια δυναμική ισορροπία στην αφθονία τόσο του λούτσου όσο και του σταυροειδούς κυπρίνου. Διατηρείται συνεχώς μια ισορροπία που θα απέκλειε την εξαφάνιση οποιουδήποτε κρίκου στην τροφική αλυσίδα (Εικ. 64).[ ...]
Ας προχωρήσουμε στην πιο σημαντική γενίκευση, δηλαδή ότι οι αρνητικές αλληλεπιδράσεις γίνονται λιγότερο αισθητές με την πάροδο του χρόνου εάν το οικοσύστημα είναι αρκετά σταθερό και η χωρική του δομή επιτρέπει την αμοιβαία προσαρμογή των πληθυσμών. Σε μοντέλα συστημάτων όπως αρπακτικό-θήραμα, που περιγράφεται από την εξίσωση Lotka-Volterra, εάν δεν εισαχθούν πρόσθετοι όροι στην εξίσωση, οι οποίοι χαρακτηρίζουν την επίδραση των παραγόντων της αυτοπεριοριζόμενης αφθονίας, τότε οι διακυμάνσεις συμβαίνουν συνεχώς και δεν σβήνουν (βλ. Levontin, 1969). Ο Pimentel (1968, βλέπε επίσης Pimentel and Stone 1968) έδειξε πειραματικά ότι τέτοιοι πρόσθετοι όροι μπορεί να αντικατοπτρίζουν αμοιβαίες προσαρμογές ή γενετικές ανατροφοδότηση. Όταν δημιουργήθηκαν νέοι πολιτισμοί από άτομα που προηγουμένως συνυπήρχαν σε μια κουλτούρα για δύο χρόνια, όπου ο αριθμός τους υπόκειτο σε σημαντικές διακυμάνσεις, αποδείχθηκε ότι ανέπτυξαν μια οικολογική ομοιόσταση, στην οποία ο καθένας από τους πληθυσμούς «καταστέλλονταν» από τον άλλο. σε τέτοιο βαθμό που αποδείχθηκε η συνύπαρξή τους σε μια πιο σταθερή ισορροπία.
Μοντέλο κατάστασης τύπου «αρπακτικό-θήραμα».
Ας εξετάσουμε ένα μαθηματικό μοντέλο της δυναμικής της συνύπαρξης δύο βιολογικών ειδών (πληθυσμών) που αλληλεπιδρούν μεταξύ τους σύμφωνα με τον τύπο «αρπακτικού-θηράματος» (λύκοι και κουνέλια, λούτσοι και σταυροειδείς κυπρίνοι κ.λπ.), που ονομάζεται Voltaire- Μοντέλο Lotka. Αποκτήθηκε για πρώτη φορά από τον A. Lotka (1925), και λίγο αργότερα, και ανεξάρτητα από τον Lotka, αναπτύχθηκαν παρόμοια και πιο σύνθετα μοντέλα από τον Ιταλό μαθηματικό V. Volterra (1926), του οποίου το έργο ουσιαστικά έθεσε τα θεμέλια της που ονομάζεται μαθηματική οικολογία.
Ας υποθέσουμε ότι υπάρχουν δύο βιολογικά είδη που ζουν μαζί σε ένα απομονωμένο περιβάλλον. Αυτό προϋποθέτει:
- 1. Το θύμα μπορεί να βρει αρκετό φαγητό για να ζήσει.
- 2. Σε κάθε συνάντηση του θύματος με το αρπακτικό, ο τελευταίος σκοτώνει το θύμα.
Για βεβαιότητα, θα τα ονομάσουμε σταυροειδείς και λούτσους. Αφήνω
η κατάσταση του συστήματος καθορίζεται από τις ποσότητες x(t)Και y(t)- ο αριθμός των σταυροειδών και των λούτσων αυτή τη στιγμή ΣΟΛ.Για να λάβουμε μαθηματικές εξισώσεις που περιγράφουν κατά προσέγγιση τη δυναμική (μεταβολή στο χρόνο) του πληθυσμού, προχωράμε ως εξής.
Όπως και στο προηγούμενο μοντέλο αύξησης του πληθυσμού (βλ. Ενότητα 1.1), για τα θύματα έχουμε την εξίσωση
Οπου ΕΝΑ> 0 (το ποσοστό γεννήσεων υπερβαίνει το ποσοστό θνησιμότητας)
Συντελεστής ΕΝΑη αύξηση του θηράματος εξαρτάται από τον αριθμό των αρπακτικών (μειώνεται με την αύξησή τους). Στην πιο απλή περίπτωση a- a - fjy (a>0, p>0).Τότε για το μέγεθος του πληθυσμού των θηραμάτων έχουμε τη διαφορική εξίσωση
Για τον πληθυσμό των αρπακτικών, έχουμε την εξίσωση

Οπου σι>0 (η θνησιμότητα υπερβαίνει το ποσοστό γεννήσεων).
Συντελεστής σιΗ εξαφάνιση των αρπακτικών μειώνεται εάν υπάρχει θήραμα για να τραφεί. Στην πιο απλή περίπτωση, μπορεί κανείς να πάρει b - y -Sx (y > 0, μικρό> 0). Στη συνέχεια για το μέγεθος του πληθυσμού των αρπακτικών λαμβάνουμε τη διαφορική εξίσωση

Έτσι, οι εξισώσεις (1.5) και (1.6) αντιπροσωπεύουν ένα μαθηματικό μοντέλο του εξεταζόμενου προβλήματος της αλληλεπίδρασης πληθυσμού. Σε αυτό το μοντέλο, οι μεταβλητές x,y- η κατάσταση του συστήματος και οι συντελεστές χαρακτηρίζουν τη δομή του. Το μη γραμμικό σύστημα (1.5), (1.6) είναι το μοντέλο Voltaire-Lotka.
Οι εξισώσεις (1.5) και (1.6) θα πρέπει να συμπληρωθούν με αρχικές συνθήκες - δεδομένες τιμές των αρχικών πληθυσμών.
Ας αναλύσουμε τώρα το κατασκευασμένο μαθηματικό μοντέλο.
Ας κατασκευάσουμε το πορτρέτο φάσης του συστήματος (1.5), (1.6) (σύμφωνα με την έννοια του προβλήματος Χ> 0, v >0). Διαιρώντας την εξίσωση (1.5) με την εξίσωση (1.6), παίρνουμε μια εξίσωση με χωριστές μεταβλητές
Χρησιμοποιώντας αυτή την εξίσωση, θα έχουμε
Η σχέση (1.7) δίνει την εξίσωση των τροχιών φάσης σε άρρητη μορφή. Το σύστημα (1.5), (1.6) έχει μια στατική κατάσταση που καθορίζεται από

Από τις εξισώσεις (1.8) παίρνουμε (επειδή l* φά 0, y* φά 0)
Οι ισότητες (1.9) καθορίζουν τη θέση ισορροπίας στο επίπεδο φάσης (το σημείο ΣΧΕΤΙΚΑ ΜΕ)(Εικόνα 1.6).

Η κατεύθυνση της κίνησης κατά μήκος της τροχιάς φάσης μπορεί να προσδιοριστεί από τέτοιες εκτιμήσεις. Ας είναι λίγος ο κυπρίνος. g.u. x ~ 0, μετά από την εξίσωση (1.6) y
Όλες οι τροχιές φάσης (με εξαίρεση το σημείο 0) κλειστές καμπύλες που περικλείουν τη θέση ισορροπίας. Η κατάσταση ισορροπίας αντιστοιχεί σε σταθερό αριθμό x' και y' σταυροειδών και λούτσων. Οι κυπρίνοι αναπαράγονται, οι λούτσοι τους τρώνε, πεθαίνουν, αλλά ο αριθμός αυτών και άλλων δεν αλλάζει. "Οι τροχιές κλειστής φάσης αντιστοιχούν σε μια περιοδική αλλαγή στον αριθμό των σταυροειδών και των λούτσων. Επιπλέον, η τροχιά κατά την οποία κινείται το σημείο φάσης εξαρτάται από τις αρχικές συνθήκες. Εξετάστε πώς αλλάζει η κατάσταση κατά μήκος της τροχιάς φάσης. Αφήστε το σημείο να είναι στη θέση του ΕΝΑ(Εικ. 1.6). Υπάρχουν λίγοι κυπρίνοι εδώ, πολλοί λούτσοι. οι λούτσοι δεν έχουν τίποτα να φάνε και σταδιακά σβήνουν και σχεδόν
εξαφανιστεί εντελώς. Αλλά και ο αριθμός του σταυροειδούς κυπρίνου μειώνεται σχεδόν στο μηδέν και
μόνο αργότερα, όταν ο λούτσος έγινε λιγότερο από στο, αρχίζει η αύξηση του αριθμού των σταυροφόρων. Ο ρυθμός ανάπτυξής τους αυξάνεται και ο αριθμός τους αυξάνεται - αυτό συμβαίνει περίπου στο σημείο ΣΕ.Αλλά η αύξηση του αριθμού του σταυροειδούς κυπρίνου οδηγεί σε επιβράδυνση της διαδικασίας εξαφάνισης του shuk και ο αριθμός τους αρχίζει να αυξάνεται (υπάρχει περισσότερη τροφή) - οικόπεδο Ήλιος.Επιπλέον, υπάρχουν πολλοί λούτσοι, τρώνε σταυροειδές κυπρίνο και τρώνε σχεδόν όλους τους (ενότητα CD).Μετά από αυτό, οι λούτσοι αρχίζουν να σβήνουν ξανά και η διαδικασία επαναλαμβάνεται με μια περίοδο περίπου 5-7 ετών. Στο σχ. 1.7 ποιοτικά κατασκευασμένες καμπύλες μεταβολών στον αριθμό των σταυροειδών και λούτσων ανάλογα με το χρόνο. Τα μέγιστα των καμπυλών εναλλάσσονται και τα μέγιστα αφθονίας του λούτσου υστερούν σε σχέση με αυτά του σταυροειδούς κυπρίνου.

Αυτή η συμπεριφορά είναι χαρακτηριστική για διάφορα συστήματα αρπακτικών-θηραμάτων. Ας ερμηνεύσουμε τώρα τα αποτελέσματα που προέκυψαν.
Παρά το γεγονός ότι το εξεταζόμενο μοντέλο είναι το πιο απλό και στην πραγματικότητα όλα συμβαίνουν πολύ πιο περίπλοκα, κατέστησε δυνατή την εξήγηση ορισμένων από τα μυστηριώδη πράγματα που υπάρχουν στη φύση. Οι ιστορίες των ψαράδων για τις περιόδους που «οι λούτσοι πέφτουν στα χέρια τους» είναι κατανοητές, η συχνότητα των χρόνιων ασθενειών κ.λπ., έχει εξηγηθεί.
Ας σημειώσουμε ακόμη ένα ενδιαφέρον συμπέρασμα, το οποίο μπορεί να κατασκευαστεί από το Σχ. 1.6. Αν στο σημείο Rυπάρχει μια γρήγορη σύλληψη λούτσων (με άλλη ορολογία - πυροβολισμός λύκων), τότε το σύστημα "πηδά" στο σημείο Q,και περαιτέρω κίνηση συμβαίνει κατά μήκος μιας μικρότερης κλειστής τροχιάς, η οποία είναι διαισθητικά αναμενόμενη. Αν μειώσουμε τον αριθμό των λούτσων στο σημείο R,τότε το σύστημα θα πάει στο σημείο ΜΙΚΡΟ,και περαιτέρω κίνηση θα συμβεί κατά μήκος της τροχιάς μεγαλύτερο μέγεθος. Το πλάτος της ταλάντωσης θα αυξηθεί. Αυτό είναι αντίθετο με τη διαίσθηση, αλλά απλώς εξηγεί ένα τέτοιο φαινόμενο: ως αποτέλεσμα του πυροβολισμού λύκων, ο αριθμός τους αυξάνεται με το χρόνο. Έτσι, η επιλογή της στιγμής λήψης είναι σημαντική σε αυτή την περίπτωση.
Ας υποθέσουμε ότι δύο πληθυσμοί εντόμων (για παράδειγμα, μια αφίδα και μια πασχαλίτσα που τρώει αφίδες) βρίσκονταν σε φυσική ισορροπία. x-x*, y = y*(τελεία ΣΧΕΤΙΚΑ ΜΕστο Σχ. 1.6). Εξετάστε τον αντίκτυπο μιας και μόνο εφαρμογής ενός εντομοκτόνου που σκοτώνει x> 0 των θυμάτων και y > 0 των αρπακτικών χωρίς να τους καταστρέψει εντελώς. Η μείωση του αριθμού και των δύο πληθυσμών οδηγεί στο γεγονός ότι το αντιπροσωπευτικό σημείο από τη θέση ΣΧΕΤΙΚΑ ΜΕ«πηδά» πιο κοντά στην καταγωγή, όπου x > 0, y 0 (Εικ. 1.6) Συνεπάγεται ότι ως αποτέλεσμα της δράσης ενός εντομοκτόνου σχεδιασμένου να καταστρέφει θύματα (αφίδες), ο αριθμός των θυμάτων (αφίδες) αυξάνεται και ο αριθμός των αρπακτικών ( πασχαλίτσες) μειώνεται. Αποδεικνύεται ότι ο αριθμός των αρπακτικών μπορεί να γίνει τόσο μικρός που θα εξαφανιστούν εντελώς για άλλους λόγους (ξηρασία, ασθένειες κ.λπ.). Έτσι, η χρήση εντομοκτόνων (εκτός αν καταστρέφουν σχεδόν πλήρως τα επιβλαβή έντομα) οδηγεί τελικά σε αύξηση του πληθυσμού των εντόμων των οποίων ο αριθμός ελεγχόταν από άλλα αρπακτικά εντόμων. Τέτοιες περιπτώσεις περιγράφονται σε βιβλία για τη βιολογία.
Σε γενικές γραμμές, ο ρυθμός αύξησης του αριθμού των θυμάτων ΕΝΑεξαρτάται τόσο από το L" όσο και από το y: ΕΝΑ= a(x, y) (λόγω της παρουσίας αρπακτικών και περιορισμών στα τρόφιμα).
Με μια μικρή αλλαγή στο μοντέλο (1.5), (1.6), προστίθενται μικροί όροι στη δεξιά πλευρά των εξισώσεων (λαμβάνοντας υπόψη, για παράδειγμα, τον ανταγωνισμό των σταυροειδών για φαγητό και των λούτσων για σταυροειδείς)
εδώ 0 f.i « 1.
Σε αυτή την περίπτωση, το συμπέρασμα σχετικά με την περιοδικότητα της διαδικασίας (επιστροφή του συστήματος στην αρχική κατάσταση), που ισχύει για το μοντέλο (1.5), (1.6), χάνει την ισχύ του. Ανάλογα με τον τύπο των μικρών διορθώσεων / και σολΟι καταστάσεις που φαίνονται στο Σχ. 1.8.

Στην περίπτωση (1) η κατάσταση ισορροπίας ΣΧΕΤΙΚΑ ΜΕσταθερά. Για οποιεσδήποτε άλλες αρχικές συνθήκες, μετά από αρκετά μεγάλη ώραείναι εγκατεστημένο.
Στην περίπτωση (2) το σύστημα «πάει στο πάτωμα». Η στατική κατάσταση είναι ασταθής. Ένα τέτοιο σύστημα τελικά εμπίπτει σε ένα τέτοιο εύρος τιμών Χκαι y ότι το μοντέλο δεν είναι πλέον εφαρμόσιμο.
Στην περίπτωση (3) σε σύστημα με ασταθή στατική κατάσταση ΣΧΕΤΙΚΑ ΜΕο περιοδικός τρόπος καθιερώνεται με την πάροδο του χρόνου. Σε αντίθεση με το αρχικό μοντέλο (1.5), (1.6), σε αυτό το μοντέλο το σταθερό περιοδικό καθεστώς δεν εξαρτάται από τις αρχικές συνθήκες. Αρχικά μικρή απόκλιση από τη σταθερή κατάσταση ΣΧΕΤΙΚΑ ΜΕοδηγεί σε μικρές διακυμάνσεις ΣΧΕΤΙΚΑ ΜΕ, όπως στο μοντέλο Volterra-Lotka, αλλά σε ταλαντώσεις ενός καλά καθορισμένου (και ανεξάρτητου από τη μικρότητα της απόκλισης) πλάτους.
ΣΕ ΚΑΙ. Ο Arnold αποκαλεί το μοντέλο Volterra-Lotka άκαμπτο, γιατί Η μικρή αλλαγή του μπορεί να οδηγήσει σε συμπεράσματα διαφορετικά από αυτά που δίνονται παραπάνω. Για να κρίνουμε ποια από τις καταστάσεις που υποδεικνύονται στο Σχ. Το 1.8, που εφαρμόζεται σε αυτό το σύστημα, είναι απολύτως απαραίτητο Επιπλέον πληροφορίεςσχετικά με το σύστημα (σχετικά με τη μορφή μικρών διορθώσεων / και σολ).
Εδώ, σε αντίθεση με το (3.2.1), τα πρόσημα (-012) και (+a2i) είναι διαφορετικά. Όπως και στην περίπτωση του ανταγωνισμού (σύστημα εξισώσεων (2.2.1)), η αρχή (1) για αυτό το σύστημα είναι ένα μοναδικό σημείο του τύπου «ασταθής κόμβος». Τρεις άλλες πιθανές στατικές καταστάσεις:

Το βιολογικό νόημα απαιτεί θετικές τιμές X y x 2. Για την έκφραση (3.3.4) αυτό σημαίνει ότι
Αν ο συντελεστής ενδοειδικού ανταγωνισμού των αρπακτικών ΕΝΑ,22 = 0, η συνθήκη (3.3.5) οδηγεί στη συνθήκη ai2
Πιθανοί τύποι πορτρέτων φάσης για το σύστημα εξισώσεων (3.3.1) φαίνονται στο σχήμα. 3.2 α-γ. Οι ισοκλίνες των οριζόντιων εφαπτομένων είναι ευθείες
και οι ισοκλίνες των κατακόρυφων εφαπτομένων είναι ευθείες
Από το σχ. Το 3.2 δείχνει τα ακόλουθα. Το σύστημα αρπακτικών-θηραμάτων (3.3.1) μπορεί να έχει μια σταθερή ισορροπία στην οποία ο πληθυσμός των θηραμάτων έχει εξαφανιστεί πλήρως (x = 0) και παρέμειναν μόνο αρπακτικά (σημείο 2 στο Σχ. 3.26). Προφανώς, μια τέτοια κατάσταση μπορεί να πραγματοποιηθεί μόνο εάν, εκτός από τον τύπο των θυμάτων που εξετάζουμε, Χαρπακτικό Χ2 έχει επιπλέον τροφοδοτικά. Αυτό το γεγονός αντικατοπτρίζεται στο μοντέλο από τον θετικό όρο στη δεξιά πλευρά της εξίσωσης για το xs. Τα μοναδικά σημεία (1) και (3) (Εικ. 3.26) είναι ασταθή. Η δεύτερη πιθανότητα είναι μια σταθερή ακίνητη κατάσταση, στην οποία ο πληθυσμός των αρπακτικών εξαφανίστηκε εντελώς και παρέμειναν μόνο θύματα - ένα σταθερό σημείο (3) (Εικ. 3.2α). Εδώ το μοναδικό σημείο (1) είναι επίσης ένας ασταθής κόμβος.
Τέλος, η τρίτη πιθανότητα είναι η σταθερή συνύπαρξη πληθυσμών αρπακτικών και θηραμάτων (Εικ. 3.2 γ), των οποίων οι στάσιμοι αριθμοί εκφράζονται με τους τύπους (3.3.4). Ας εξετάσουμε αυτή την περίπτωση με περισσότερες λεπτομέρειες.
Ας υποθέσουμε ότι οι συντελεστές ενδοειδικού ανταγωνισμού είναι ίσοι με μηδέν (Όλα συμπεριλαμβάνονται= 0, i = 1, 2). Ας υποθέσουμε επίσης ότι τα αρπακτικά τρέφονται μόνο με θήραμα του είδους Χκαι ελλείψει αυτών εξαφανίζονται με ρυθμό C2 (στο (3.3.5) C2
Ας κάνουμε μια λεπτομερή μελέτη αυτού του μοντέλου, χρησιμοποιώντας την πιο ευρέως αποδεκτή σημείωση στη βιβλιογραφία. Ανακαινισμένο

Ρύζι. 3.2. Η θέση των κύριων ισοκλινών στο πορτρέτο φάσης του συστήματος Volterra θηρευτής-θηράματος για διαφορετικές αναλογίες παραμέτρων: ΕΝΑ- σχετικά με -
ΜΕΕγώ Γ2Γ2
1, 3 - ασταθές, 2 - σταθερό μοναδικό σημείο. V -
1, 2, 3 - ασταθές, 4 - σταθερό ενικό σημείο σημαντικό
Το σύστημα αρπακτικών-θηραμάτων σε αυτές τις σημειώσεις έχει τη μορφή:

Θα μελετήσουμε τις ιδιότητες των λύσεων στο σύστημα (3.3.6) στο επίπεδο φάσης Ν1
ΕΠΙ2
Το σύστημα έχει δύο σταθερές λύσεις. Είναι εύκολο να προσδιοριστούν εξισώνοντας τις δεξιές πλευρές του συστήματος με το μηδέν. Παίρνουμε: 
Εξ ου και οι σταθερές λύσεις:

Ας ρίξουμε μια πιο προσεκτική ματιά στη δεύτερη λύση. Ας βρούμε το πρώτο ολοκλήρωμα του συστήματος (3.3.6) που δεν περιέχει t.Πολλαπλασιάστε την πρώτη εξίσωση με -72, τη δεύτερη με -71 και προσθέστε τα αποτελέσματα. Παίρνουμε:
Τώρα διαιρούμε την πρώτη εξίσωση με Νκαι πολλαπλασιάστε με € 2, και διαιρέστε το δεύτερο με JV 2 και πολλαπλασιάστε με μι.Ας προσθέσουμε ξανά τα αποτελέσματα:
Συγκρίνοντας τα (3.3.7) και (3.3.8), θα έχουμε:

Ενσωματώνοντας, παίρνουμε:

Αυτό είναι το επιθυμητό πρώτο ολοκλήρωμα. Έτσι, το σύστημα (3.3.6) είναι συντηρητικό, αφού έχει το πρώτο ολοκλήρωμα κίνησης, μια ποσότητα που είναι συνάρτηση των μεταβλητών του συστήματος ΝΚαι Ν2 και ανεξάρτητα από το χρόνο. Αυτή η ιδιότητα καθιστά δυνατή την κατασκευή ενός συστήματος εννοιών για συστήματα Volterra παρόμοιο με τη στατιστική μηχανική (βλ. Κεφάλαιο 5), όπου ουσιαστικό ρόλο παίζει το μέγεθος της ενέργειας του συστήματος, το οποίο είναι αμετάβλητο στο χρόνο.
Για κάθε διορθωμένο γ > 0 (που αντιστοιχεί σε ορισμένα αρχικά δεδομένα), το ολοκλήρωμα αντιστοιχεί σε μια συγκεκριμένη τροχιά στο επίπεδο Ν1 ΕΠΙ2 , που χρησιμεύει ως η τροχιά του συστήματος (3.3.6).
Σκεφτείτε γραφικό τρόποκατασκευή της τροχιάς, που πρότεινε ο ίδιος ο Volterra. σημειώσε ότι δεξί μέροςΟ τύπος (3.3.9) εξαρτάται μόνο από το D r 2 και ο αριστερός εξαρτάται μόνο από Ν.Δείχνω
Από την (3.3.9) προκύπτει ότι μεταξύ ΧΚαι Υυπάρχει αναλογική σχέση
Στο σχ. Το 3.3 δείχνει τα πρώτα τεταρτημόρια τεσσάρων συστημάτων συντεταγμένων XOY, NOY, Ν2 ΒΟΔΙκαι Δ Ζ 1 0Ν2 ώστε όλοι να έχουν κοινή καταγωγή.
Στην επάνω αριστερή γωνία (τεταρτημ NOY)κατασκευάζεται η γραφική παράσταση της συνάρτησης (3.3.8), κάτω δεξιά (τεταρτημόριο Ν2 βόδι)- γράφημα συνάρτησης Υ.Η πρώτη συνάρτηση έχει min at Νι =και το δεύτερο - max at Ν2 = ?-
Τέλος, στο τεταρτημόριο XOYκατασκευάστε τη γραμμή (3.3.12) για κάποια σταθερά ΜΕ.
Σημειώστε ένα σημείο Νστον άξονα ΕΠΙ. Αυτό το σημείο αντιστοιχεί σε μια συγκεκριμένη τιμή Υ(Ν 1), το οποίο είναι εύκολο να βρεθεί σχεδιάζοντας μια κάθετο

Ρύζι. 3.3.
διά μέσου Νμέχρι να τέμνεται με την καμπύλη (3.3.10) (βλ. Εικ. 3.3). Με τη σειρά του, η τιμή του K(A^) αντιστοιχεί σε κάποιο σημείο M της ευθείας Υ = cXκαι ως εκ τούτου κάποια αξία X(N) = Y(N)/cπου μπορούμε να βρούμε σχεδιάζοντας κάθετες ΕΙΜΑΙΚαι MD.Η τιμή που βρέθηκε (αυτό το σημείο σημειώνεται στο σχήμα με το γράμμα ΡΕ)ταιριάζουν δύο βαθμούς RΚαι σολστην καμπύλη (3.3.11). Με αυτά τα σημεία, σχεδιάζοντας κάθετες, βρίσκουμε δύο σημεία ταυτόχρονα ΜΙ"Και μι" που βρίσκεται στην καμπύλη (3.3.9). Οι συντεταγμένες τους είναι:

Σχέδιο κάθετο ΕΙΜΑΙ, έχουμε διασχίσει την καμπύλη (3.3.10) σε ένα ακόμη σημείο ΣΕ.Αυτό το σημείο αντιστοιχεί στο ίδιο RΚαι Qστην καμπύλη (3.3.11) και το ίδιο ΝΚαι SCH.Συντεταγμένη Ναυτό το σημείο μπορεί να βρεθεί ρίχνοντας την κάθετο από ΣΕανά άξονα ΕΠΙ.Έτσι παίρνουμε βαθμούς ΦΑ"και F" που βρίσκεται επίσης στην καμπύλη (3.3.9).
Ερχόμενος από άλλο σημείο Ν,Με τον ίδιο τρόπο λαμβάνουμε ένα νέο τετραπλό σημείων που βρίσκονται στην καμπύλη (3.3.9). Η εξαίρεση είναι η τελεία Ni= ?2/72- Με βάση αυτό, παίρνουμε μόνο δύο βαθμούς: ΠΡΟΣ ΤΗΝΚαι ΜΕΓΑΛΟ.Αυτά θα είναι τα κάτω και τα πάνω σημεία της καμπύλης (3.3.9).
Δεν μπορεί να προέρχεται από αξίες Ν, και από τις αξίες Ν2 . Κατεύθυνση από Ν2 στην καμπύλη (3.3.11), μετά ανεβαίνοντας στην ευθεία Υ = cX, και από εκεί διασχίζοντας την καμπύλη (3.3.10), βρίσκουμε επίσης τέσσερα σημεία της καμπύλης (3.3.9). Η εξαίρεση είναι η τελεία Όχι=?1/71- Με βάση αυτό, παίρνουμε μόνο δύο βαθμούς: σολΚαι ΠΡΟΣ ΤΗΝ.Αυτά θα είναι τα πιο αριστερά και δεξιά σημεία της καμπύλης (3.3.9). Ρωτώντας διαφορετικά ΝΚαι Ν2 και έχοντας λάβει αρκετά σημεία, συνδέοντάς τα, κατασκευάζουμε κατά προσέγγιση την καμπύλη (3.3.9).
Από την κατασκευή φαίνεται ότι πρόκειται για μια κλειστή καμπύλη που περιέχει μέσα της το σημείο 12 = (?2/721? Ν yu και N20. Λαμβάνοντας μια άλλη τιμή του C, δηλ. άλλα αρχικά δεδομένα, παίρνουμε μια άλλη κλειστή καμπύλη που δεν τέμνει την πρώτη και περιέχει επίσης το σημείο (?2/721?1/71)1 μέσα της. Έτσι, η οικογένεια των τροχιών (3.3.9) είναι η οικογένεια των κλειστών γραμμών που περιβάλλουν το σημείο 12 (βλ. Εικ. 3.3). Διερευνούμε τον τύπο της σταθερότητας αυτού του μοναδικού σημείου χρησιμοποιώντας τη μέθοδο Lyapunov.
Αφού όλες οι παράμετροι μι 1, ?2, 71,72 είναι θετικά, τελεία (Το N[ βρίσκεται στο θετικό τεταρτημόριο του επιπέδου φάσης. Η γραμμικοποίηση του συστήματος κοντά σε αυτό το σημείο δίνει:

Εδώ n(t)και 7i2(N1, Ν2 :
Χαρακτηριστική εξίσωση του συστήματος (3.3.13):

Οι ρίζες αυτής της εξίσωσης είναι καθαρά φανταστικές:

Έτσι, η μελέτη του συστήματος δείχνει ότι οι τροχιές κοντά στο μοναδικό σημείο αντιπροσωπεύονται από ομόκεντρες ελλείψεις, και το ίδιο το μοναδικό σημείο είναι το κέντρο (Εικ. 3.4). Το υπό εξέταση μοντέλο Volterra έχει επίσης κλειστές τροχιές μακριά από το μοναδικό σημείο, αν και το σχήμα αυτών των τροχιών διαφέρει ήδη από το ελλειψοειδές. Μεταβλητή συμπεριφορά Νι, Ν2 στο χρόνο φαίνεται στο Σχ. 3.5.

Ρύζι. 3.4.

Ρύζι. 3.5. Η εξάρτηση του αριθμού των θηραμάτων Νεγώ και αρπακτικό Ν2 από τον χρόνο
Ένα μοναδικό σημείο κέντρου τύπου είναι σταθερό, αλλά όχι ασυμπτωτικά. Ας χρησιμοποιήσουμε αυτό το παράδειγμα για να δείξουμε τι είναι. Αφήστε τις δονήσεις Κόνιδα ψείρας)και LGgM εμφανίζονται με τέτοιο τρόπο ώστε το αντιπροσωπευτικό σημείο να κινείται κατά μήκος του επιπέδου φάσης κατά μήκος της τροχιάς 1 (βλ. Εικ. 3.4). Τη στιγμή που το σημείο βρίσκεται στη θέση Μ, ένας ορισμένος αριθμός ατόμων προστίθεται στο σύστημα από έξω Ν 2 έτσι ώστε το αντιπροσωπευτικό σημείο να μεταπηδά από το σημείο Μσημείο Α/". Μετά από αυτό, αν το σύστημα αφεθεί ξανά στον εαυτό του, οι ταλαντώσεις NiΚαι Ν2 θα συμβεί ήδη με μεγαλύτερα πλάτη από πριν και το αντιπροσωπευτικό σημείο κινείται κατά μήκος της τροχιάς 2. Αυτό σημαίνει ότι οι ταλαντώσεις στο σύστημα είναι ασταθείς: αλλάζουν τα χαρακτηριστικά τους για πάντα όταν εξωτερική επιρροή. Στη συνέχεια, εξετάζουμε μοντέλα που περιγράφουν σταθερά καθεστώτα ταλάντωσης και δείχνουμε ότι τέτοιες ασυμπτωτικές σταθερές περιοδικές κινήσεις αναπαρίστανται στο επίπεδο φάσης μέσω οριακών κύκλων.
Στο σχ. Το 3.6 δείχνει πειραματικές καμπύλες - διακυμάνσεις στον αριθμό των γουνοφόρων ζώων στον Καναδά (σύμφωνα με την Hudson's Bay Company). Αυτές οι καμπύλες χτίζονται με βάση τα δεδομένα για τον αριθμό των συγκομισμένων δερμάτων. Οι περίοδοι διακυμάνσεων στον αριθμό των λαγών (θηράματα) και λύγκων (αρπακτικών) είναι περίπου ίδιες και είναι της τάξης των 9-10 ετών. Ταυτόχρονα, ο μέγιστος αριθμός λαγών, κατά κανόνα, είναι μπροστά από τον μέγιστο αριθμό λύγκα κατά ένα χρόνο.
Το σχήμα αυτών των πειραματικών καμπυλών είναι πολύ λιγότερο σωστό από τις θεωρητικές. Ωστόσο, σε αυτή την περίπτωση, αρκεί το μοντέλο να διασφαλίζει τη σύμπτωση των πιο σημαντικών χαρακτηριστικών της θεωρητικής και πειραματικής καμπύλης, δηλ. τιμές πλάτους και μετατόπιση φάσης μεταξύ των διακυμάνσεων στον αριθμό των αρπακτικών και των θηραμάτων. Ένα πολύ πιο σοβαρό μειονέκτημα του μοντέλου Volterra είναι η αστάθεια των λύσεων στο σύστημα των εξισώσεων. Πράγματι, όπως προαναφέρθηκε, οποιαδήποτε τυχαία αλλαγή στην αφθονία του ενός ή του άλλου είδους θα πρέπει να οδηγεί, σύμφωνα με το μοντέλο, σε αλλαγή στο πλάτος των ταλαντώσεων και των δύο ειδών. Φυσικά, σε φυσικές συνθήκεςτα ζώα υπόκεινται σε αμέτρητες τέτοιες τυχαίες επιρροές. Όπως φαίνεται από τις πειραματικές καμπύλες, το εύρος των διακυμάνσεων στον αριθμό των ειδών ποικίλλει ελάχιστα από έτος σε έτος.
Το μοντέλο Volterra είναι ένα (βασικό) μοντέλο αναφοράς για τη μαθηματική οικολογία στον ίδιο βαθμό που το μοντέλο του αρμονικού ταλαντωτή είναι βασικό για την κλασική και κβαντική μηχανική. Με τη βοήθεια αυτού του μοντέλου, που βασίζεται σε πολύ απλοποιημένες ιδέες για τη φύση των προτύπων που περιγράφουν τη συμπεριφορά του συστήματος, καθαρά μαθηματικά
κεφάλαιο 3

Ρύζι. 3.6. Κινητικές καμπύλες της αφθονίας των γουνοφόρων ζώων Σύμφωνα με την Hudson's Bay Fur Company (Seton-Thomson, 1987), εξήχθη ένα συμπέρασμα με λογισμό σχετικά με την ποιοτική φύση της συμπεριφοράς ενός τέτοιου συστήματος - σχετικά με την παρουσία διακυμάνσεων του πληθυσμού σε ένα τέτοιο σύστημα. Χωρίς την κατασκευή ενός μαθηματικού μοντέλου και τη χρήση του, ένα τέτοιο συμπέρασμα θα ήταν αδύνατο.
Στα προαναφερθέντα απλή φόρμαΤο σύστημα Volterra έχει δύο θεμελιώδεις και αλληλένδετες ελλείψεις. Η «εξάλειψή» τους είναι αφιερωμένη σε εκτενή οικολογική και μαθηματική βιβλιογραφία. Πρώτον, η συμπερίληψη στο μοντέλο οποιωνδήποτε, αυθαίρετα μικρών, πρόσθετων παραγόντων αλλάζει ποιοτικά τη συμπεριφορά του συστήματος. Το δεύτερο «βιολογικό» μειονέκτημα του μοντέλου είναι ότι δεν περιλαμβάνει τις θεμελιώδεις ιδιότητες που είναι εγγενείς σε οποιοδήποτε ζεύγος πληθυσμών που αλληλεπιδρούν σύμφωνα με την αρχή αρπακτικού-θηράματος: την επίδραση του κορεσμού του αρπακτικού, τους περιορισμένους πόρους του αρπακτικού και του θηράματος ακόμη και με περίσσεια θηράματος, δυνατότητα ελάχιστου αριθμού θηραμάτων διαθέσιμο για αρπακτικό κ.λπ.
Προκειμένου να εξαλειφθούν αυτά τα μειονεκτήματα, έχουν προταθεί διάφορες τροποποιήσεις του συστήματος Volterra από διαφορετικούς συγγραφείς. Τα πιο ενδιαφέροντα από αυτά θα εξεταστούν στην Ενότητα 3.5. Εδώ μένουμε μόνο σε ένα μοντέλο που λαμβάνει υπόψη τους αυτοπεριορισμούς στην αύξηση και των δύο πληθυσμών. Το παράδειγμα αυτού του μοντέλου δείχνει ξεκάθαρα πώς μπορεί να αλλάξει η φύση των λύσεων όταν αλλάζουν οι παράμετροι του συστήματος.
Θεωρούμε λοιπόν το σύστημα

Το σύστημα (3.3.15) διαφέρει από το προηγουμένως θεωρημένο σύστημα (3.3.6) από την παρουσία όρων της μορφής -7 στη δεξιά πλευρά των εξισώσεων uNf,
Αυτά τα μέλη αντικατοπτρίζουν το γεγονός ότι ο πληθυσμός των θηραμάτων δεν μπορεί να αυξάνεται επ 'αόριστον ακόμη και απουσία αρπακτικών λόγω περιορισμένων πόρων τροφίμων, περιορισμένου εύρους ύπαρξης. Οι ίδιοι «αυτοπεριορισμοί» επιβάλλονται και στον πληθυσμό των αρπακτικών.
Για να βρείτε τους σταθερούς αριθμούς των ειδών iVi και Ν2 ισοδυναμούν με μηδέν τα δεξιά μέρη των εξισώσεων του συστήματος (3.3.15). Λύσεις με μηδενικό αριθμό αρπακτικών ή θηραμάτων δεν θα μας ενδιαφέρουν τώρα. Επομένως, σκεφτείτε ένα αλγεβρικό σύστημα
εξισώσεις  Η απόφασή της
Η απόφασή της
μας δίνει τις συντεταγμένες του ενικού σημείου. Εδώ, η συνθήκη της θετικότητας των στατικών αριθμών θα πρέπει να τεθεί στις παραμέτρους του συστήματος: Ν> 0 και Ν2 > 0. Οι ρίζες της χαρακτηριστικής εξίσωσης ενός συστήματος γραμμικοποιημένου σε γειτονιά ενός μοναδικού σημείου (3.3.16):

Από την έκφραση για τους χαρακτηριστικούς αριθμούς φαίνεται ότι αν η συνθήκη
τότε οι αριθμοί των αρπακτικών και των θηραμάτων εκτελούν απόσβεση ταλαντώσεων στο χρόνο, το σύστημα έχει ένα μη μηδενικό ενικό σημείο και μια σταθερή εστίαση. Το πορτρέτο φάσης ενός τέτοιου συστήματος φαίνεται στο Σχ. 3,7 α.
Ας υποθέσουμε ότι οι παράμετροι στην ανισότητα (3.3.17) αλλάζουν τις τιμές τους με τέτοιο τρόπο ώστε η συνθήκη (3.3.17) να γίνεται ισότητα. Τότε οι χαρακτηριστικοί αριθμοί του συστήματος (3.3.15) είναι ίσοι και το μοναδικό σημείο του θα βρίσκεται στο όριο μεταξύ των περιοχών σταθερών εστιών και κόμβων. Όταν το πρόσημο της ανισότητας (3.3.17) αντιστραφεί, το ενικό σημείο γίνεται σταθερός κόμβος. Το πορτρέτο φάσης του συστήματος για αυτήν την περίπτωση φαίνεται στο Σχ. 3.76.
Όπως και στην περίπτωση ενός μεμονωμένου πληθυσμού, ένα στοχαστικό μοντέλο μπορεί να αναπτυχθεί για το μοντέλο (3.3.6), αλλά δεν μπορεί να επιλυθεί ρητά. Επομένως, περιοριζόμαστε σε γενικές σκέψεις. Ας υποθέσουμε, για παράδειγμα, ότι το σημείο ισορροπίας βρίσκεται σε κάποια απόσταση από κάθε έναν από τους άξονες. Στη συνέχεια για τροχιές φάσης στις οποίες οι τιμές του JVj, Ν2 παραμένει αρκετά μεγάλο, ένα ντετερμινιστικό μοντέλο θα είναι αρκετά ικανοποιητικό. Αν όμως κάποια στιγμή


Ρύζι. 3.7. Πορτραίτο φάσης του συστήματος (3.3.15): ΕΝΑ -όταν πληρούται η σχέση (3.3.17) μεταξύ των παραμέτρων. σι- κατά την εκτέλεση της αντίστροφης σχέσης μεταξύ των παραμέτρων
τροχιά φάσης, οποιαδήποτε μεταβλητή δεν είναι πολύ μεγάλη, τότε οι τυχαίες διακυμάνσεις μπορεί να γίνουν σημαντικές. Οδηγούν στο γεγονός ότι το αντιπροσωπευτικό σημείο θα μετακινηθεί σε έναν από τους άξονες, που σημαίνει την εξαφάνιση του αντίστοιχου είδους. Έτσι, το στοχαστικό μοντέλο αποδεικνύεται ασταθές, αφού η στοχαστική «παρασυρόμενη» αργά ή γρήγορα οδηγεί στην εξαφάνιση ενός από τα είδη. Σε αυτό το είδος μοντέλου, το αρπακτικό τελικά πεθαίνει, είτε τυχαία είτε επειδή ο πληθυσμός του θηράματος εξαλείφεται πρώτα. Το στοχαστικό μοντέλο του συστήματος αρπακτικών-θηραμάτων εξηγεί καλά τα πειράματα του Gause (Gause, 1934; 2000), στα οποία βλεφαρίδες Paramettum candatumχρησίμευε ως θήραμα για ένα άλλο βλεφαροφόρο Didinium nasatum- αρπακτικό. Οι αναμενόμενοι αριθμοί ισορροπίας σύμφωνα με τις ντετερμινιστικές εξισώσεις (3.3.6) σε αυτά τα πειράματα ήταν περίπου μόνο πέντε άτομα από κάθε είδος, επομένως δεν υπάρχει τίποτα περίεργο στο γεγονός ότι σε κάθε επαναλαμβανόμενο πείραμα, είτε τα αρπακτικά είτε τα θηράματα πέθαναν αρκετά γρήγορα (και στη συνέχεια αρπακτικά). ).
Έτσι, η ανάλυση των μοντέλων Volterra αλληλεπίδρασης ειδών δείχνει ότι, παρά τη μεγάλη ποικιλία των τύπων συμπεριφοράς τέτοιων συστημάτων, δεν μπορούν να υπάρξουν καθόλου αμετάβλητες πληθυσμιακές διακυμάνσεις στο μοντέλο των ανταγωνιστικών ειδών. Στο μοντέλο θηρευτή-θηράματος, εμφανίζονται ταλαντώσεις χωρίς απόσβεση λόγω της επιλογής ειδική φόρμαεξισώσεις μοντέλου (3.3.6). Σε αυτή την περίπτωση, το μοντέλο γίνεται μη τραχύ, γεγονός που υποδηλώνει την απουσία μηχανισμών σε ένα τέτοιο σύστημα που επιδιώκουν να διατηρήσουν την κατάστασή του. Ωστόσο, τέτοιες διακυμάνσεις παρατηρούνται στη φύση και στο πείραμα. Η ανάγκη για τη θεωρητική τους εξήγηση ήταν ένας από τους λόγους για τη διατύπωση περιγραφών μοντέλων σε περισσότερα γενική εικόνα. Η ενότητα 3.5 είναι αφιερωμένη στην εξέταση τέτοιων γενικευμένων μοντέλων.






